
- •1. Основные понятия
- •1.1. Волновое уравнение для электромагнитного поля
- •1.2. Плоская электромагнитная волна
- •1.3. Энергия электромагнитных волн
- •1.4. Шкала электромагнитных волн
- •2. Световая волна
- •2.1. Показатель преломления среды
- •2.2. Интенсивность света
- •3. Энергетические и фотометрические величины и единицы
- •Примечание. Укажем для примера, что сила света лампы накаливания мощностью 1 Вт составляет примерно 55-75 кд, сила света свечи близка к 1 кд.
ТЕМА № 18 (2лц+2пр+8ср)
ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
1. Основные понятия
Из электродинамики известно, что переменное электрическое поле порождает магнитное, которое, вообще говоря, тоже оказывается переменным. Это переменное магнитное поле порождает электрическое и т. д. Таким образом, если возбудить с помощью колеблющихся зарядов переменное магнитное поле, то в окружающем заряды пространстве возникнет последовательность взаимных превращений электрического и магнитного полей, распространяющихся от точки к точке. Этот процесс будет периодическим во времени и в пространстве и, следовательно, представляет собой волну.
1.1. Волновое уравнение для электромагнитного поля
Существование электромагнитных волн вытекает из уравнений Максвелла для электромагнитного поля. Волновые уравнения имеют вид
 ,
(1.1)
,
(1.1)
 .
(1.2)
.
(1.2)
Здесь
Δ=∂2/∂x2+∂2/∂y2+∂2/∂z2
― оператор Лапласа;
 и
и
 ― напряженность электрического и
магнитного полей, соответственно; в
системе СИ единица напряженности
электрического поля имеет название
вольт на метр
и обозначается В/м. Единица напряженности
магнитного поля в СИ носит название
ампер на метр
[А/м];
― напряженность электрического и
магнитного полей, соответственно; в
системе СИ единица напряженности
электрического поля имеет название
вольт на метр
и обозначается В/м. Единица напряженности
магнитного поля в СИ носит название
ампер на метр
[А/м];
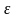 и
и
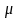 ― диэлектрическая и магнитная
проницаемости, соответственно; величины
и
являются безразмерными. Диэлектрическая
проницаемость
показывает, во сколько раз ослабляется
электрическое поле в диэлектрике.
Магнитная проницаемость
показывает, во сколько раз усиливается
магнитное поле в магнетике;
― диэлектрическая и магнитная
проницаемости, соответственно; величины
и
являются безразмерными. Диэлектрическая
проницаемость
показывает, во сколько раз ослабляется
электрическое поле в диэлектрике.
Магнитная проницаемость
показывает, во сколько раз усиливается
магнитное поле в магнетике;
 и
и
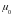 ― электрическая и магнитная постоянные.
Величина
имеет размерность электрической емкости,
деленной на длину. Соответственно ее
выражают в единицах, называемых фарад
на метр
[Ф/м]. Числовое значение
― электрическая и магнитная постоянные.
Величина
имеет размерность электрической емкости,
деленной на длину. Соответственно ее
выражают в единицах, называемых фарад
на метр
[Ф/м]. Числовое значение
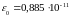 Ф/м. В свою очередь величина
имеет размерность индуктивности,
деленной на длину. Эту величину выражают
в единицах, называемых генри
на метр
[Гн/м]. Числовое значение
Ф/м. В свою очередь величина
имеет размерность индуктивности,
деленной на длину. Эту величину выражают
в единицах, называемых генри
на метр
[Гн/м]. Числовое значение
 Гн/м.
Гн/м.
Полагая, что

 (1.3)
(1.3)
есть
скорость
электромагнитных волн в вакууме,
числовое значение которой
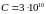 м/с и принимая во внимание известное
волновое уравнение для упругой среды
м/с и принимая во внимание известное
волновое уравнение для упругой среды
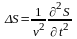 ,
(1.4)
,
(1.4)
где
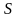 ― физическая величина, которая
характеризует возмущение, распространяющееся
в среде с фазовой скоростью v,
имеем
― физическая величина, которая
характеризует возмущение, распространяющееся
в среде с фазовой скоростью v,
имеем
 .
(1.5)
.
(1.5)
Выражение
(1.5) показывает, что фазовая скорость
электромагнитных волн в среде зависит
от диэлектрической проницаемости
 и магнитной проницаемости
и магнитной проницаемости
 среды. В вакууме (т.е. при
среды. В вакууме (т.е. при
 )
скорость электромагнитных волн совпадает
со скоростью света в вакууме С.
)
скорость электромагнитных волн совпадает
со скоростью света в вакууме С.
1.2. Плоская электромагнитная волна
Исследуем
плоскую электромагнитную волну,
распространяющуюся в нейтральной
непроводящей среде с постоянными
проницаемостями
и
.
Направим ось
 перпендикулярно к волновым поверхностям.
Тогда
и
,
а значит, и их компоненты по координатным
осям не будут зависеть от координат
перпендикулярно к волновым поверхностям.
Тогда
и
,
а значит, и их компоненты по координатным
осям не будут зависеть от координат
 и
и
 .
.
Волновые
уравнения для
 и
и
 имеют вид, соответственно
имеют вид, соответственно
 ,
(1.6)
,
(1.6)
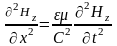 .
(1.7)
.
(1.7)
Полученные уравнения представляют собой частный случай уравнений (1.1) и (1.2).
Отметим,
что
 и
и
 ,
поэтому
,
поэтому
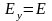 и
и
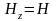 .
В уравнениях (1.6) и (1.7) при
и
сохранены индексы
и
,
чтобы подчеркнуть то обстоятельство,
что векторы
и
направлены вдоль взаимно перпендикулярных
осей
и
.
.
В уравнениях (1.6) и (1.7) при
и
сохранены индексы
и
,
чтобы подчеркнуть то обстоятельство,
что векторы
и
направлены вдоль взаимно перпендикулярных
осей
и
.
Простейшим решением уравнений (1.6) и (1.7) являются функции
 ,
(1.8)
,
(1.8)
 .
(1.9)
.
(1.9)
В
этих формулах
 - частота волны,
- частота волны,
 - волновое число, равное
- волновое число, равное
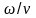 ,
,
 и
и
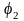 ― начальные фазы колебаний в точках с
координатой
― начальные фазы колебаний в точках с
координатой
 .
.
Колебания
электрического и магнитного векторов
в электромагнитной волне происходят с
одинаковой фазой (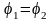 ),
а амплитуды этих векторов связаны
соотношением
),
а амплитуды этих векторов связаны
соотношением
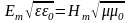 .
(1.10)
.
(1.10)
В векторной форме уравнения плоской электромагнитной волны имеют вид:
 ,
(1.11)
,
(1.11)
 .
(1.12)
.
(1.12)
На
рис. 1.1 показана "моментальная фотография"
плоской электромагнитной волны. Из
рисунка видно, что векторы
и
образуют с
направлением распространения волны
правовинтовую систему.
В фиксированной точке пространства
векторы
и
изменяются со
временем
показана "моментальная фотография"
плоской электромагнитной волны. Из
рисунка видно, что векторы
и
образуют с
направлением распространения волны
правовинтовую систему.
В фиксированной точке пространства
векторы
и
изменяются со
временем
по гармоническому закону. Они одновременно увеличиваются от нуля, затем через 1/4 периода достигают наибольшего значения, причем, если направлен вверх, то направлен вправо (смотрим вдоль направления, по которому распространяется волна). Еще через 1/4 периода оба вектора одновременно обращаются в нуль. Затем опять достигают максимального значения, но на этот раз направлен вниз, а влево. И, наконец, по завершении периода колебания векторы снова обращаются в нуль. Такие изменения векторов и происходят во всех точках пространства, но со сдвигом по фазе, определяемым расстоянием между точками, отсчитанными вдоль оси .
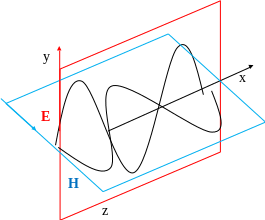
Рисунок 1.1. Компоненты электромагнитной волны
