Примеры вычисления разности потенциалов по напряженности поля

Поле равномерно заряженной бесконечной плоскости

Х₁

Х₂

,

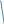
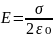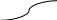где – поверхностная плотность

заряда, т.е. заряда, приходящегося на

единицу поверхности.

Разность потенциалов между точками, лежащими на расстояниях Х₁ и Х₂ от плоскости, равна

П

E₁

оле равномерно заряженной сферической поверхности

Радиус сферы R, общий заряд Q

r₂

E₂

R

r₁

При r˃R:

Разность потенциалов между двумя точками, лежащими на расстояниях r₁ и r₂ от центра сферы (r₁˃R, r₂>R), равна Е=0 (r<R)

(x)

Е сли принять r₁=rи r₂= , то потенциал поля вне сферической поверхности задается выражением

П оле объемно заряженного шара

R

r₂

Е

Объемная

r₁

r

r

плотность

0

r

заряда

Радиус шара R, общий заряд Q.

П ри r>Rразность потенциалов между двумя точками вне шара определяется по формуле для сферической поверхности (x).

В любой точке, лежащий внутри шара напряженность определяется выражением r

Разность потенциалов между двумя точками, лежащими на расстояниях r₁ и r₂ от центра шара (r₁<R, r₂<R), равна

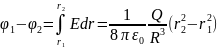
П оле равномерно заряженного бесконечного цилиндра

E

r

l

R

Радиус цилиндра R, заряжен с линейной плотностью , внецилиндра ( >R) напряженность определяется формулой

, ( )

Следовательно, разность потенциалов между двумя точками, лежащими на расстояниях r₁и r₂ от оси заряженного цилиндра (r₁<R , r₂>R), равна

8. Электростатическое поле электрического диполя в вакууме

8.1. Электрический диполь

Простейшей системой точечных зарядов является электрический диполь (двойной полюс). Так называется совокупность равных по модулю, но противоположных по знаку двух точечных зарядов и , сдвинутых друг относительно друга на некоторое расстояние (рис. 5).

Рисунок 5. Электрический диполь

Рисунок 6. Дипольный момент

Плечом диполя называется вектор направленный по оси диполя ( прямой, проходящей через центры обоих зарядов) от отрицательного заряда к положительному и равному по модулю расстоянию между ними (рис. 6).

Электрическим моментом диполя (дипольным электрическим моментом) называется вектор , равный произведению положительного заряда диполя на плечо , т.е.

. ()

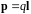Вектор совпадает по направлению с плечом диполя . Оказалось, что такая модель очень неплохо описывает электрические свойства атомов и молекул, а так же влияние на них внешнего электрического поля. Поэтому в физике широко пользуются представлением атомов и молекул в виде электрических диполей.

8.2. Примеры расчета электростатических полей с использованием представления электрического диполя

Искомая точка А расположена на оси диполя

-Q

+Q

A

Рассчитатьполе в определенной

r

точке – значит найтиEи

в этой точке!

,

В соответствии с принципом суперпозицииполей напряженность в произвольной точке диполя

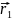где и - напряженности полей зарядов +Qи –Qв рассматриваемой точке, и – радиусы векторы, проведенные в точку А из точечных зарядов +Qи –Q, причем

Векторы и совпадают по направлению с вектором , поэтому

, ,

.

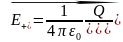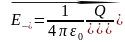Потенциал поля в точке А на основании принципа суперпозиции равен сумме потенциалов полей точечных зарядов +Qи –Q.

Используя связь напряженности и потенциала находим

Так как для поля диполя 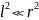, то напряженностьи потенциал поля в точке А на оси диполя равны

Искомая точка В поля находится на перпендикуляре, восстановленном к оси диполя из его середины О

В этой точке

Из рисунка видно, что

,

причем вектор параллелен электрическому моменту диполя и направлен в противоположную сторону. Следовательно, напряженность поля диполя в точке В при

Точка В равноудалена от зарядов +Qи –Q диполя, поэтому потенциал поля в точке В равен нулю

Р

асчет поля диполя в произвольной точке С с полярными координатами и 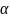удобнее всего произвести с помощью следующего вспомогательного приема.

0

N

M

K

C

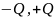
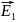
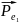
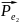
Опустим на прямую NC, соединяющую заряд –Qдиполя с точкой С, перпендикуляр МК, проведенный из точки М, где находится заряд +Q.

Поместим в точку К два точечных заряда +Qи –Q, которые полностью нейтрализуют друг друга и не искажают поля диполя.

Тогда четыре заряда, находящиеся в точках М, Nи К, можно рассматривать как два диполя (NК и МК).

Ввиду малости расстояния по сравнению с угол СNМ . Поэтому модули электрических моментов первого и второго диполей соответственно равны

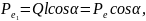
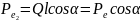
Для первого диполя точка С лежит на его оси, а для второго – на перпендикуляре, восстановленном в средней точке оси.

По уже известным нам формулам напряженности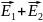 полей каждого из диполей в точке С равны

,

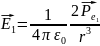Векторы и , соответственно и , взаимно перпендикулярны, поэтому модуль напряженности поля диполя МNв точке С

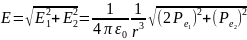
Подставив сюда значения и , получим

Потенциал поля диполя в точке С равен сумме потенциалов в этой точке для полей двух диполей (NК и МК):

,

где и находятся по известным нам формулам.

Таким образом