
11 Клас
1. Чи існують дійсні числа , що задовольняють рівність:
 ?
?
Відповідь: не існують.
Розв’язання.
Позначимо
 ,
,
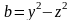 ,
тоді
,
тоді
 і задана рівність переписується таким
чином:
і задана рівність переписується таким
чином:

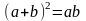

 .
.
З
останнього маємо, що ця рівність можлива
лише при
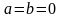 ,
що неможливо внаслідок умов задачі.
Таким чином задана рівність не можлива.
,
що неможливо внаслідок умов задачі.
Таким чином задана рівність не можлива.
2.
Знайдіть
усі такі натуральні числа
 ,
які мають більше
,
які мають більше
 дільників.
дільників.
(Рубльов Богдан)
Відповідь:
 .
.
Розв’язання.
Зрозуміло, що число не може мати дільників,
більших від
,
окрім самого числа
.
Тому, щоб мати більше дільників, ніж
воно повинно ділитись на усі числа від
до
та на число
.
Позначимо через
те з двох чисел
чи
 ,
яке є цілим. Тоді при
,
яке є цілим. Тоді при
 одне з чисел
або
одне з чисел
або
 взаємно просте з
.
Тому
взаємно просте з
.
Тому
 ,
оскільки воно повинно ділитись на
та на
одночасно. Але тоді
,
оскільки воно повинно ділитись на
та на
одночасно. Але тоді
 тобто
тобто
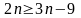 ,
що суперечить умові
.
Для випадку
,
що суперечить умові
.
Для випадку
 числа перевіряються безпосередньо.
числа перевіряються безпосередньо.
3. Відомо, що многочлен
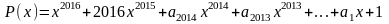
можна
також подати у вигляді
 ,
де серед чисел
,
де серед чисел
 принаймні 2015 від’ємних та не обов’язково
різних. Знайдіть усі коефіцієнти
многочлену
принаймні 2015 від’ємних та не обов’язково
різних. Знайдіть усі коефіцієнти
многочлену
 .
.
(Голоднов Кирило)
Відповідь.
 ,
,
 .
.
Розв’язання.
Без обмеження загальності будемо
вважати, що
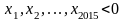 .
Звідси за теоремою Вієта для многочленів
(або просто із заданого розкладу
многочлену на множники)
.
Звідси за теоремою Вієта для многочленів
(або просто із заданого розкладу
многочлену на множники)
 .
Тому значення
.
Тому значення
 також дійсне та від’ємне. Далі з теореми
Вієта маємо:
також дійсне та від’ємне. Далі з теореми
Вієта маємо:



З нерівності між середнім арифметичним та геометричним:
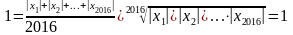 .
.
З рівності між середнім арифметичним та середнім геометричним випливає, що
 ,
тобто
,
тобто
 ,
,
тому
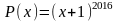 ,
звідки маємо, що
,
,
звідки маємо, що
,
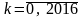 .
.

4.
В гострокутному
трикутнику
 сторони
сторони
 і
мають різну довжину, а продовження
медіани
і
мають різну довжину, а продовження
медіани
 перетинає описане коло в точці
перетинає описане коло в точці
 .
На цьому колі відмітимо таку точку
.
На цьому колі відмітимо таку точку
 ,
що
,
що
 ,
де
,
де
 – точка перетину висот трикутника
.
Точка
обрана таким чином, що
– точка перетину висот трикутника
.
Точка
обрана таким чином, що
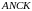 - паралелограм. Доведіть, що прямі
- паралелограм. Доведіть, що прямі
 ,
,
 і
і
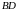 перетинаються в одній точці.
перетинаються в одній точці.
(Нагель Ігор)
Р
Рис. 10
озв’язання. Нехай – точка перетину висот і
і
 трикутника
.
Точки
трикутника
.
Точки
 ,
,
,
,
 ,
і
,
і
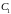 лежать на одному колі з діаметром
лежать на одному колі з діаметром
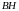 ,
бо
,
бо
 (рис. 10).
(рис. 10).
Далі,
так як чотирикутники
 і
і
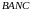 – вписані, то
– вписані, то
 і
і
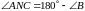 .
Звідси випливає, що
.
Звідси випливає, що
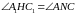 .
Але
.
Але
 (як вертикальні) і
(як вертикальні) і
 (як протилежні кути паралелограма. Тому
одержуємо, що
(як протилежні кути паралелограма. Тому
одержуємо, що
 ,
тобто чотирикутник
,
тобто чотирикутник
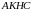 – вписаний. Звідси випливає, що
– вписаний. Звідси випливає, що
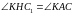 .
Далі,
.
Далі,
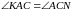 ,
бо
,
бо
 ,
а
,
а
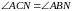 ,
бо ці кути – вписані в описане коло
трикутника
.
Отже,
,
бо ці кути – вписані в описане коло
трикутника
.
Отже,
 ,
а це означає, що точка
,
а це означає, що точка
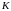 також належить колу з діаметром
.
також належить колу з діаметром
.
Позначимо
через
 – описане коло трикутника
,
через
– описане коло трикутника
,
через
 – коло з діаметром
,
а через
– коло з діаметром
,
а через
 – описане коло чотирикутника
.
Тоді
,
і
– радикальні осі кіл
і
,
і
,
та
і
.
Як відомо: радикальні осі трьох кіл
перетинаються в одній точці – радикальному
центрі трьох кіл, або паралельні.
– описане коло чотирикутника
.
Тоді
,
і
– радикальні осі кіл
і
,
і
,
та
і
.
Як відомо: радикальні осі трьох кіл
перетинаються в одній точці – радикальному
центрі трьох кіл, або паралельні.
Оскільки
 ,
то прямі
,
і
перетинаються в одній точці.
,
то прямі
,
і
перетинаються в одній точці.
5 .
У країні є
2015 міст, деякі з яких з’єднані двосторонніми
авіалініями. Відомо, що для кожного
.
У країні є
2015 міст, деякі з яких з’єднані двосторонніми
авіалініями. Відомо, що для кожного
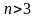 не існує
попарно різних міст
не існує
попарно різних міст
 ,
для яких існував би замкнений маршрут
перельотів
,
для яких існував би замкнений маршрут
перельотів
 (для трьох міст такі маршрути можуть
існувати). Яка найбільша кількість пар
міст цієї країни можуть бути з’єднані
прямим авіасполученням?
(для трьох міст такі маршрути можуть
існувати). Яка найбільша кількість пар
міст цієї країни можуть бути з’єднані
прямим авіасполученням?
(Рубльов Богдан)
Відповідь:
 .
.
Розв’язання. Перепишемо умову задачі мовою графів.
Граф
складається з вершин
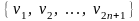 та ребер
та ребер
 ,
які з’єднують деякі з вершин. Циклом
довжини
у цьому графі назвемо таку послідовність
ребер
,
які з’єднують деякі з вершин. Циклом
довжини
у цьому графі назвемо таку послідовність
ребер
 ,
,
 ,
...,
,
...,
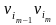 ,
,
 де
де
 ,
,
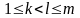 .
Відомо, що у графі немає циклів довжини
більше 3-х. Скільки максимум у цього
графі може бути ребер?
.
Відомо, що у графі немає циклів довжини
більше 3-х. Скільки максимум у цього
графі може бути ребер?
Спочатку
покажемо, що існує граф, що задовольняє
умови та має
 вершин. Він зображений на рис. 11.
вершин. Він зображений на рис. 11.
Доведемо, що ця величина є максимальною.
Очевидно, що граф зв’язний, якщо ні, то достатньо провести ребро між будь-якими двома компонентами зв’язності і умова про цикли не зміниться, а кількість ребер збільшиться.
П означимо
через
означимо
через
 – кількість ребер найкоротшого шляху,
що з’єднує відповідні вершини, а через
– кількість ребер найкоротшого шляху,
що з’єднує відповідні вершини, а через
 – найбільшу можливе значення для усіх
– найбільшу можливе значення для усіх
 .
.
Розглянемо граф, у якому кількість ребер є максимальною. Серед усіх таких графів виберемо той, у якого мінімальне значення приймає величина .
Припустимо,
що
 .
Нехай один з найдовших шляхів складається
з послідовних вершин
.
Нехай один з найдовших шляхів складається
з послідовних вершин
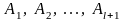 ,
,
 .
.
Р озглянемо
вершину
озглянемо
вершину
 .
Якщо вона має степінь
(висяча вершина, рис. 12), тобто ребро
.
Якщо вона має степінь
(висяча вершина, рис. 12), тобто ребро
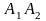 – єдине, що проходить через вершину
.
Тоді ми просто замість ребра
проведемо ребро
– єдине, що проходить через вершину
.
Тоді ми просто замість ребра
проведемо ребро
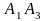 .
При цьому довжина найдовшого шляху
зменшиться. Вчинимо таким чином з усіма
висячими вершинами усіх найдовших
шляхів. Припустимо знову, що
і шлях утворюють вершини
,
.
.
При цьому довжина найдовшого шляху
зменшиться. Вчинимо таким чином з усіма
висячими вершинами усіх найдовших
шляхів. Припустимо знову, що
і шлях утворюють вершини
,
.
Нехай
окрім ребра
існує ребро
 .
При цьому можливі такі випадки.
.
При цьому можливі такі випадки.
Існує
також ребро
 (рис.13). Тоді міняємо граф таким чином –
замість ребер
та
проводимо ребра
та
(рис.13). Тоді міняємо граф таким чином –
замість ребер
та
проводимо ребра
та
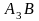 .
При цьому і тут довжина найдовшого шляху
скоротиться.
.
При цьому і тут довжина найдовшого шляху
скоротиться.
Р ебра
не існує. Найкоротший шлях від
до
ебра
не існує. Найкоротший шлях від
до
 не може проходити через вершини
не може проходити через вершини
 ,
бо його довжина більша від
.
Тому існує інший шлях від
до
.
Але тоді
зв’язана принаймні з однією з вершин
,
бо його довжина більша від
.
Тому існує інший шлях від
до
.
Але тоді
зв’язана принаймні з однією з вершин
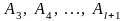 ,
нехай перша з вершин, яка зустрічається
на найкоротшому шляху між
та
– це
,
нехай перша з вершин, яка зустрічається
на найкоротшому шляху між
та
– це
 ,
,
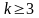 .
Тоді маємо цикл
.
Тоді маємо цикл
 ,
який має більше 3 ланок. Одержана
суперечність показує неможливість
цього випадку.
,
який має більше 3 ланок. Одержана
суперечність показує неможливість
цього випадку.
Таким
чином можемо вважати, що
 .
Припустимо, що немає вершини, що має
степінь
.
Припустимо, що немає вершини, що має
степінь
 .
Виберемо вершину
,
що має максимальну степінь
.
Виберемо вершину
,
що має максимальну степінь
 ,
тоді існує вершина
,
яка не зв’язана з
(рис. 14). Тоді найкоротший шлях від
до
дорівнює
,
тоді існує вершина
,
яка не зв’язана з
(рис. 14). Тоді найкоротший шлях від
до
дорівнює
 ,
оскільки
.
Нехай цей шлях буде
,
оскільки
.
Нехай цей шлях буде
 .
Якщо існує вершина
,
для якої існують ребра
та
.
Якщо існує вершина
,
для якої існують ребра
та
 ,
то утворюється цикл довжини
,
то утворюється цикл довжини
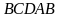 .
Тоді виберемо довільну вершину
,
що з’єднана з
та не з’єднана з
.
Тоді повинне бути ребро
.
Тоді виберемо довільну вершину
,
що з’єднана з
та не з’єднана з
.
Тоді повинне бути ребро
 ,
бо інакше найкоротший шлях між
та
буде більше
.
Але це означає, що степінь вершини
більше ніж у
,
оскільки вона ще з’єднана з
,
на відміну від
.
Або для наступної вершини
,
для якої існує
,
бо інакше найкоротший шлях між
та
буде більше
.
Але це означає, що степінь вершини
більше ніж у
,
оскільки вона ще з’єднана з
,
на відміну від
.
Або для наступної вершини
,
для якої існує
 та
та
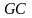 маємо цикл
маємо цикл
 – суперечність.
– суперечність.
Таким
чином існує вершина, позначимо її через
 .
Вона зв’язана з кожною іншою вершиною.
Якщо степінь деякої з інших вершин
.
Вона зв’язана з кожною іншою вершиною.
Якщо степінь деякої з інших вершин
 більше
,
тобто існують ребра
та
більше
,
тобто існують ребра
та
 ,
де
,
де
 .
Але тоді маємо заборонений цикл
.
Але тоді маємо заборонений цикл
 ,
оскільки
з’єднана з усіма іншими вершинами.
,
оскільки
з’єднана з усіма іншими вершинами.
Тому окрім усі інші вершини можуть мати степінь не більше . Але це й призводить на до прикладу на рис. 1, де й маємо максимальну кількість ребер.
Альтернативне розв’язання. (Лішунов Віталій)
Відповідь:
 .
.
Розв’яжемо задачу для довільної кількості вершин .
Нехай
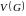 і
і
 − кількість вершин і ребер графа
− кількість вершин і ребер графа
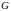 відповідно, і позначимо через
відповідно, і позначимо через
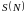 максимум ребер, які може мати граф
,
який задовольняє умову задачі і
максимум ребер, які може мати граф
,
який задовольняє умову задачі і
 .
Доведемо індукцією по
,
що
.
Доведемо індукцією по
,
що
 .
Базі індукції безпосередньо перевіряється
при
.
Базі індукції безпосередньо перевіряється
при
 .
Припустимо, що ми довели твердження для
всіх
.
Припустимо, що ми довели твердження для
всіх
 ,
при
,
при
 ,
і доведемо його для
.
,
і доведемо його для
.
Якщо
граф не має циклів, то кількість його
ребер дорівнює
 ,
де
,
де
 кількість компонент зв’язності графа
.
В такому випадку,
кількість компонент зв’язності графа
.
В такому випадку,
 і твердження доведене.
і твердження доведене.
Нехай
тепер граф
має цикл. За умовою, довжина цього циклу
дорівнює
 і тому можемо вважати, що його утворюють
вершини
і тому можемо вважати, що його утворюють
вершини
 ,
,
 і
і
 .
Розглянемо граф
.
Розглянемо граф
 ,
який утворений з графа
вилученням ребер, що сполучають ці
вершини. Помітимо, що
,
і
належать різним компонентам зв’язності
графа
.
Справді, якщо це не так, то хоча б дві
вершини, нехай
і
,
належать одній компоненті зв’язності,
а тому існує простий шлях
,
який утворений з графа
вилученням ребер, що сполучають ці
вершини. Помітимо, що
,
і
належать різним компонентам зв’язності
графа
.
Справді, якщо це не так, то хоча б дві
вершини, нехай
і
,
належать одній компоненті зв’язності,
а тому існує простий шлях
 ,
,
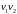 ,
…,
,
…,
 у якого
у якого
 ,
,
 .
.
Якщо
 ,
то маємо простий цикл
,
то маємо простий цикл
 ,
,
…,
,
,
…,
 ,
,
 ,
довжина якого не менша за
,
довжина якого не менша за
 ,
що суперечить умові.
,
що суперечить умові.
Якщо
 ,
то граф
має цикл
,
,
то граф
має цикл
,
 ,
,
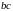 ,
,
 ,
довжина якого дорівнює
,
що також не можливо.
,
довжина якого дорівнює
,
що також не можливо.
Якщо
 ,
то граф
має ребро
,
то граф
має ребро
 ,
яке ми вилучили.
,
яке ми вилучили.
Отже,
ми довели, що вершини
,
і
належать різним компонентам зв’язності
графа
.
Нехай
 ,
де
,
де
 − компонента зв’язності, яка містить
вершину
,
− компонента зв’язності, яка містить
вершину
,
 − компонента, що містить
,
а
− компонента, що містить
,
а
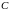 − решта вершин графа
.
Оскільки
− решта вершин графа
.
Оскільки
 і підграфи
,
і
задовольняють умову задачі, то за
припущенням індукції
і підграфи
,
і
задовольняють умову задачі, то за
припущенням індукції
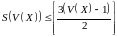 ,
при
,
при
 ,
звідки
,
звідки
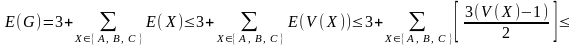
 .
.
Оскільки
нерівність
 виконується для довільного графа, який
задовольняє умову задачі, то
виконується для довільного графа, який
задовольняє умову задачі, то
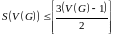 ,
тобто
,
тобто
 .
.
Залишається
побудувати приклад, для якого
 .
.
При
 можемо розглянути граф
можемо розглянути граф
 ,
,
а
при
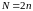 максимум досягається на графі
максимум досягається на графі
 .
.
Неважко
обчислити, що при
 маємо
маємо
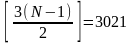 .
.
4.1.
На бісектрисі
кута
 трикутника
трикутника
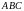 вибрали такі точки
вибрали такі точки
 ,
для яких
,
для яких
 ,
,
 .
Точка
.
Точка
 – середина відрізку
– середина відрізку
 .
Доведіть, що
.
Доведіть, що
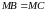 .
.
Розв’язання.
Нехай перпендикуляр з точки
 на
перетинається з ним у точці
на
перетинається з ним у точці
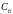 ,
аналогічно
,
аналогічно
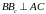 .
Нехай
.
Нехай
 – проекції точки
на прямі
та
– проекції точки
на прямі
та
 відповідно. Не обмежуючи загальності
розгляду вважаємо, що розташування
точок має вигляд як на рис. 14. Тоді:
відповідно. Не обмежуючи загальності
розгляду вважаємо, що розташування
точок має вигляд як на рис. 14. Тоді:
 та
та
 .
.
Т оді
з властивостей середньої лінії маємо,
що
оді
з властивостей середньої лінії маємо,
що
 ,
,
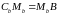 .
Тому
.
Тому
 та
та
 .
Оскільки
.
Оскільки
 та
та
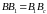 ,
то це означає, що
,
то це означає, що
 ,
звідки
,
звідки
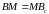 ,
тому
,
тому
 .
.
