17

ЭКСПЛУАТАЦИЯ и ремонт ОБОРУДОВАНИЯ (5 курс)

ЛЕКЦИЯ №13

Методы поиска отказов

Учебные вопросы:

1. Последовательный поиск отказов с восстановлением объекта контроля.

2. Метод последовательных элементных проверок. 

3. Прогнозирование технического состояния оборудования по результатам измерения сопротивления изоляции.

1. Последовательный поиск отказов с восстановлением объекта контроля

Метод последовательных поэлементных проверок

Рассмотрим задачу построения программы восстановления по минимуму математического ожидания затрат при условии, что имеется возможность проверки работоспособности объекта контроля.

Приближенный алгоритм при произвольных пересекающихся тестах заключается в следующем. Пусть к началу некоторого М-го шага процесса проверки проведена последовательность тестов: s(М-1)={t1,...,tM-1} и задача сводится к отысканию отказавших элементов подмножества W(М-1).

Алгоритм поиска заключается в следующем:

1) Проводится (если возможно) общий тест, чтобы определить есть ли в непроверенном подмножестве W(0) хотя бы один отказавший элемент. Если тест проходит успешно, то на этом процедура проверки прекращается, если тест проходит неуспешно, то начинается основная процедура.

2) Если глобальный тест проходит неуспешно, то для каждого теста ti вычисляется вероятность неуспешного исхода в проверяемом подмножестве:

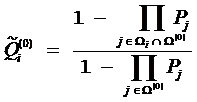 при условии, что проведена последовательность тестов s(0).

Примечание. Достаточно вычислить лишь величины:  , потому что в п.5 наибольшее значение имеют лишь относительные величины, а не абсолютные -  .

3) Для каждого теста ti находят связанные с ним затраты Сi при условии, что уже проведена последовательность тестов s(0). Перед началом процесса проверки  .

4) Для каждого теста ti определяется величина:  .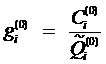

5) Выбираем такой тест tk для которого   минимально: .

6) Применяется тест tk, причем:

а) если тест завершается успешно, то процесс поиска отказавших элементов продолжается для оставшегося подмножества W(1)=W(0)\Wk;

б) тест заканчивается неуспешно, то возможны два случая:

- если тест контролирует работоспособность только одного элемента, то этот элемент заменяется годным и дальнейшее отыскание отказов производится в подмножестве W(1)=W(0)\Wk;

- если тест контролирует больше одного элемента, то дальнейший поиск отказов производится в подмножестве W(1)=Wk, причем для этого могут быть использованы лишь тесты tu, такие, что WkÈWu=Wk.

7) Фиксируется новая последовательность s(1) применяемых тестов, содержащая предыдущую последовательность s(0) и последний применяемый тест tk:s(1){s(0), tk}.

8) К подмножеству W(1), указанному в пункте 6 вновь применяется процедура проверки, начиная с пункта 1, если найденный отказавший элемент заменен на работоспособный, и начиная с пункта 2, если замена отказавшего элемента не проводилась, соответствующей заменой верхнего индекса (0) на индекс (1).

Процесс проверки продолжается до тех пор, пока не будут найдены и заменены годными все отказавшие элементы системы.

Пример 2. Система состоит из 8 элементов и может быть проверена 6-ю тестами, описание которых приводится в таблице 18.2. Известны затраты на проведение тестов: С1=1; с2=2; С3=1,2; С4=1,5; С5=2,5; С6=1,3, величина Сi не зависит от порядка применения теста.

Таблица 18.2 - Матрица тестов

Номер теста	Номер элемента
	1	2		3	4	5	6	7	8
1	1	1				1	1
2		1			1				1
3				1		1	1
4	1						1		1
5	1			1	1	1
6						1		1	1

Вероятности отказов элементов q1=0,1; q2=0,1; q3=0,2; q4=0,3; q5=0,1; q6=0,5; q7=0,5; q8=0,2; Количество отказавших элементов заранее неизвестно. Будем считать, что элементы 3, 4, и 7 неисправны, но тому, кто проводит проверку это неизвестно. Необходимо найти все отказавшие элементы при минимальных средних затратах на проведение необходимых для этого тестов.

РЕШЕНИЕ:

1) Вычисляем величины вероятностей неуспешного исхода   в проверяемом подмножестве по формуле 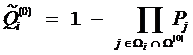 , и находим, что  ,  ,  ,  ,  , 

2) Определяем величину отношения стоимости проведения теста к величине вероятности неуспешного исхода  , по формуле  :  ;  ;  ;  ;  ;  ;

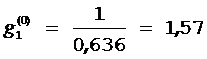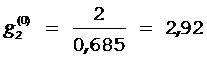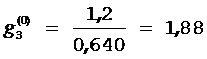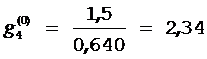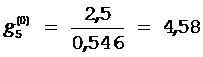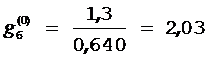Первым тестом должен быть тест t1, т. к.   минимально и равно 1,57.

Тест должен пройти успешно, т. к. в условии задачи мы определили элементы 3, 4 и 7 как отказавшие. В связи с этим задача сводится к обнаружению отказавших элементов в оставшемся подмножестве элементов W(1)={3,4,7,8}

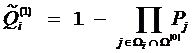3) Вычисляем величины   по формуле  , и находим, что  ,  ,  ,  ,  .

4) Определяем новые значения

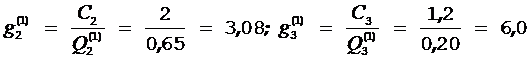
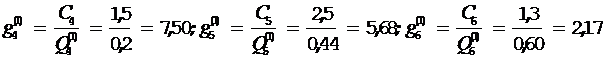
Минимальное значение   имеет тест t6, проверяющий элементы 7 и 8. По условию задачи тест оказался неуспешным (неисправны элементы 3, 4 и 7). Для дальнейшего поиска отказов в подмножестве W1 может быть использован лишь тест t2, в результате применения которого (по условию данного примера) будет сделан вывод об отказе элементов 7 или 4. Получение более детальной информации о состоянии системы применением имеющихся тестов матрицы Т оказывается невозможным, следовательно, задача обнаружения всех отказавших элементов рассматриваемого объекта и замены их работоспособными не может быть выполнена.

ДОБАВЛЕНО