КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ В ХИМИИ. ПРАКТИЧЕСКАЯ ЧАСТЬ

Примеры решения химических задач на компьютере

Попробуем решить простую химическую задачу - Составить кинетическую модель необратимой реакции второго порядка вида , если известны: начальные концентрации реагентов С_А(0) и С_В(0), кмоль/м³, константа скорости реакции к, м³/(кмольс). Получить кинетические зависимости компонентов реакции в виде графиков функций С_А(t), C_B(t), C_D(t); определить время 50%-ного превращения компонента А. Кинетические уравнения имеют вид:

для компонента А  ,

для компонента В  ,

для компонента D  . Искомые кинетические зависимости С_А(t), C_B(t), C_D(t) получаем в виде графиков, по графику С_А(t) определяем время 50%ного превращения компонента А.

В описании задания уже приведена модель процесса, состоящая из трех уравнений, остается добавить уравнение, выражающее изменение времени , где dt стремится к нулю. Согласно принципу вычисления интегралов на ЭВМ (методические указания «Компьютерное моделирование в естествознании. Часть II. Химия»), имеем систему уравнений – модель процесса:

_.

Для определения концентрации веществ в каждый момент времени, запишем уравнения в другом виде: . Другими словами, новое значение переменной – есть прежнее значение плюс его изменение:

_{Приходим к простому расчету суммы.} Необходимо составить компьютерную программу с использованием данной модели. Условием работы программы, исходя из условия задания, будет обращение в нуль либо компонента А, либо компонента В, т.к. реакция является необратимой.

Пример текста программы, написанной на языке TurboPascal 7, и результатов выполнения программы приводятся ниже.

programchim4;

usescrt, graph;

typemas= array [0..1000] ofreal;

varca0, cb0, cd0, t1, dt, k, dca, cam, cbm, cdm, max, mash:real;

ca, cb, cd,t,a,b,d,o : mas;

gd,gm,i,j,m ,im: integer;

t2:string;

proceduredan(a,b,d,t:mas ); {присвоение начальных данных и вывод на экран}

var dca,dt:real;

i,j,m:integer;

begin

ca[0]:=ca0; cb[0]:=cb0; cd[0]:=cd0; t[0]:=0;

writeln(ca[i]:8:3,cb[j]:8:3,cd[m]:8:3,t[i]:8:3);

end;

procedure graf(mash:real){(var ca,cb,cd,t:mas)};{построениеграфическихзависимостей}

var dca,dt:real;

i,j,m:integer;

begin

line(20,460,600,460);

line(20,20,20,460);

{ t[0]:=0;}

putpixel(round(20+t[0]), 460-round(ca0), 3);

putpixel(round(20+t[0]), 460-round(cb0), 5);

putpixel(round(20+t[0]), 460-round(cd0), 15);

i:=0; j:=0; m:=0;

repeat

begin

putpixel(20+round(t[i]*640/t1), 460-round(ca[i]*500/mash), 3);

setcolor(3);

outtextxy(400,200,'veshestvo A');

putpixel(20+round(t[i]), 460-round(cb[j]*500/mash), 5);

setcolor(5);

outtextxy(400,220,'veshestvo B');

putpixel(20+round(t[i]), 460-round(cd[m]*500/mash), 15);

setcolor(15);

outtextxy(400,240,'veshestvo D');

i:=i+1; j:=j+1; m:=m+1;

end;

until t[i]=t1;

str(t1,t2);

outtextxy(300,400,concat('vremya reakcii', t2));

end;

functionpmax(varo:mas):real; {определение максимального значения}

var i,im:integer;

max:real;

begin

i:=0; max:=o[i];

for i:=1 to im do

if o[i]>o[i-1] then max:=o[i];

{ writeln(max:8:3);}

pmax:=max;

end;

procedurerasc{(varca,cb,cd,t: mas)}; {расчет значений концентраций и времени}

var dca,dt,max,mash:real;

i,j,m,im:integer;

begin

ca[0]:=ca0; cb[0]:=cb0; cd[0]:=cd0; i:=1; j:=1; m:=1;

dt:=0.5; t[0]:=0;

repeat

t[i]:=t[i-1]+dt;

dca:=k*ca[i-1]*cb[j-1]*dt;

ca[i]:=ca[i-1]-dca;

cb[j]:=cb[j-1]-dca;

cd[m]:=cd[m-1]+dca;

t1:=t[i];

writeln(i,' ',ca[i]:8:3,cb[j]:8:3,cd[m]:8:3,t[i]:8:3);

i:=i+1; j:=j+1; m:=m+1;

if abs(cd[m]-cd[m-1])<=0.001 then break;

until (abs(ca[i]-ca[i-1])<=0.001);

writeln; writeln; readkey;

writeln('vremya reakcii',t1:8:3);

im:=i-1; writeln(im);

cam:=pmax(ca);

cbm:=pmax(cb);

cdm:=pmax(cd);

if cam>cbm then mash:=cam else mash:=cbm;

if cdm>mash then mash:=cdm;

writeln(mash:8:3);

readln;

clrscr;

gd:=detect; gm:=0;

initgraph(gd,gm,'F:\Зоя\диск-Адаменко\FP\BGI');

graf(mash){(ca,cb,cd,t)};

end;

begin{основная программа}

clrscr;

writeln('vvesti nach. konc. ca0, cb0 i const skorosri reakcii k');

readln(ca0,cb0,k);

cd0:=0;

writeln('N ca cb cd t');

dan(ca,cb,cd,t);

rasc{(ca,cb,cd,t)};

readln;

{clrscr;

gd:=detect; gm:=0;

initgraph(gd,gm,'F:\путькфайлу’);

i:=0;

graf(ca,cb,cd,t); }

readkey;

closegraph; end.

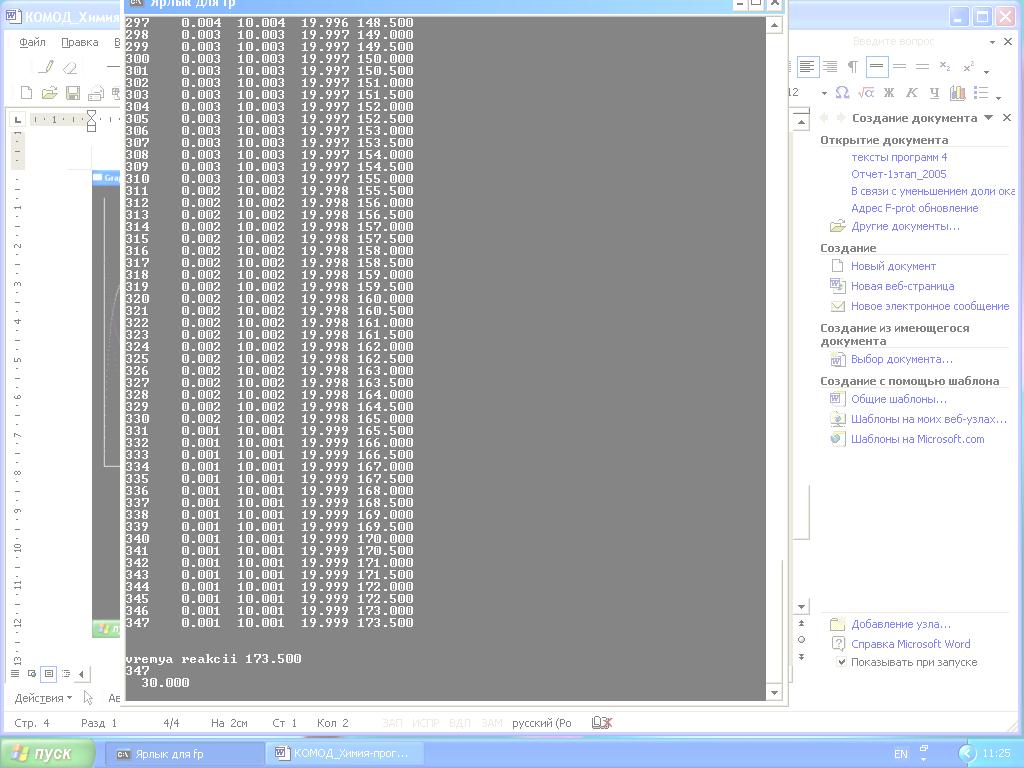
Рис. 1 Таблица результатов расчета концентраций исходных веществ А, В и продуктов реакции D от времени.

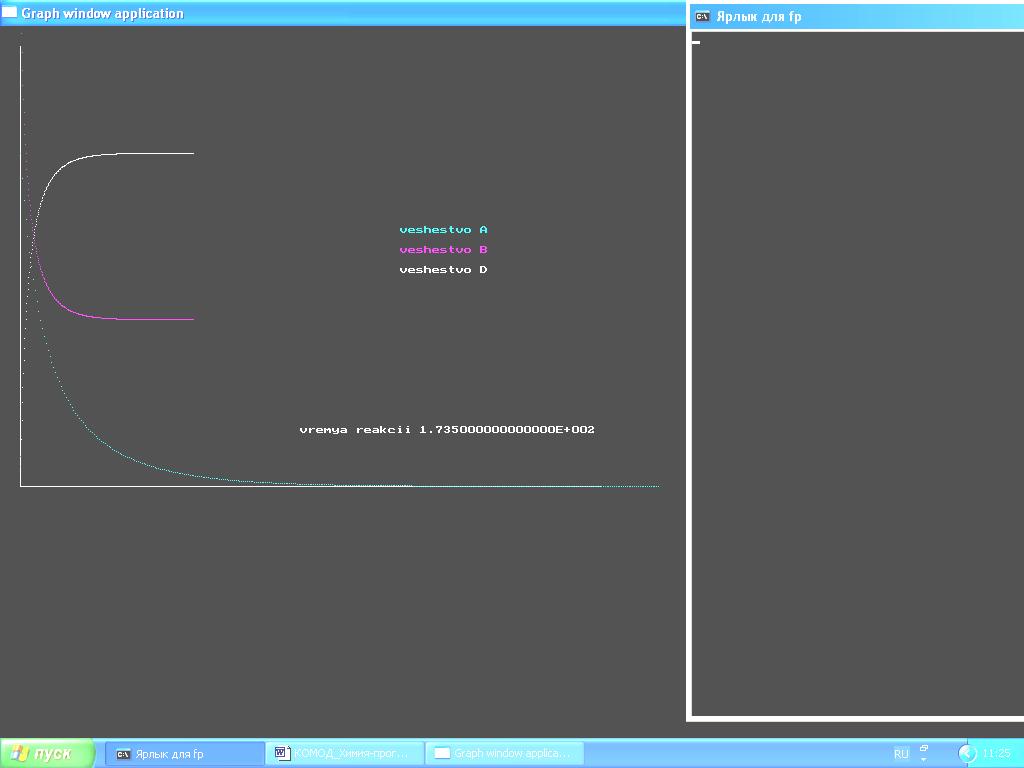
Рис. 2 Графические зависимости A(t), B(t), D(t).

Рассмотрим другой пример - необходимо получить модели простой необратимой реакции первого порядка, сложной мономолекулярной реакции, протекающей в две последовательные стадии, сложной обратимой реакции первого порядка. Получить кинетические кривые для всех компонентов химических реакций.

 получение модели необратимой реакции первого порядка вида А  В, если известны: начальные концентрации С_А(0), кмоль/м^{3, С}_В(0), кмоль/м³, константа скорости химической реакции при температурах Т₁ и Т₂. Требуется найти для каждой температуры кинетические зависимости компонентов реакции в виде функций С_А(t), С_В(t) и время 50%-ного и 80%-ного превращения компенента А.

Для моделирования запишем кинетичекие уравнения для компонента А и В

(1)

(2).

Уравнения (1) и (2) представляют систему линейных уравнений с заданными начальными условиями.

Результаты выводятся в виде таблицы, графиков С(t). Для сравнения времени 50%го и 80%го превращения компонента А с теоретическим значением применяют выражение: .

Принцип решения задачи аналогичен предыдущему. В тексте задания приведена модель, остается грамотно составить программу. Ниже приводится текст программы, реализованной в среде Delphi 7(6) и результаты выполнения программы (рис.3-5).

unitUnit1;

interface

uses

Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms, Dialogs, StdCtrls, ExtCtrls;

type

TForm1 = class(TForm)

Image1: TImage;

Edit1: TEdit;

Edit2: TEdit;

Edit3: TEdit;

Edit4: TEdit;

Edit5: TEdit;

Edit6: TEdit;

Edit7: TEdit;

Edit8: TEdit;

Label1: TLabel;

Label2: TLabel;

Label3: TLabel;

Label4: TLabel;

Label5: TLabel;

Label6: TLabel;

Label7: TLabel;

Label8: TLabel;

Button1: TButton;

Button2: TButton;

procedure Button1Click(Sender: TObject);{выполнениепрограммы}

procedure Button2Click(Sender: TObject);{очисткаэкрана}

private

{ Private declarations }

public

{ Public declarations }

end;

var

Form1: TForm1;

k1,k2,dt,c,cc:extended;

c1,c2,t:array [0..5000] of real;

i,j,k,n:integer;

implementation

{$R *.dfm}

procedure TForm1.Button1Click(Sender: TObject);

begin

C1[0]:=strtofloat(Edit1.Text);

C2[0]:=strtofloat(Edit2.Text);

k1:=strtofloat(Edit3.Text);

k2:=strtofloat(Edit4.Text);

dt:=strtofloat(Edit5.Text);

t[0]:=0; i:=0;

repeat

inc(i);

c:=c1[i-1];

cc:=c2[i-1];

c1[i]:=c1[i-1]-k1*c1[i-1]*dt;

c2[i]:=c2[i-1]+k1*c1[i-1]*dt;

t[i]:=t[i-1]+dt;

until (abs((c1[i]-c))<=0.001) or( abs((c2[i]-cc))<=0.001);

edit6.Text:=floattostr(c1[i]);

edit7.Text:=floattostr(c2[i]);

edit8.Text:=floattostr(t[i]);

for j:=0 to i do begin

with Image1.Canvas do

Pixels[round(t[j]*image1.Width/t[i]),image1.Height+10-round(c1[j]*image1.Height/c1[0])]:=clred;

with Image1.Canvas do

Pixels[round(t[j]*image1.Width/t[i]),image1.Height+10-round(c2[j]*image1.Height/c1[0])]:=clblack;

end;

edit6.Text:=floattostr(c1[i]);

edit7.Text:=floattostr(c2[i]);

edit8.Text:=floattostr(t[i]);

end;

procedure TForm1.Button2Click(Sender: TObject);

begin

for k:=0 to 405 do

for n:=0 to 331 do

image1.Canvas.Pixels[k,n]:=clwhite;

edit6.Text:='';

edit7.Text:='';

edit8.Text:='';

end;end.

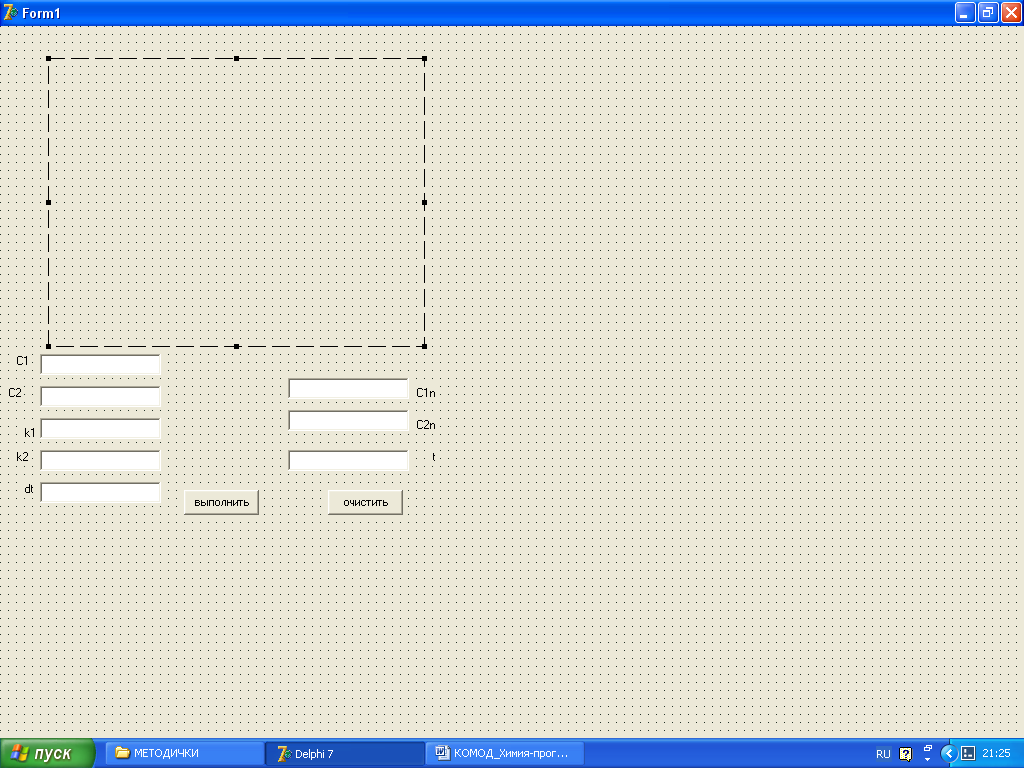
Рис. 3 Форма к программе.

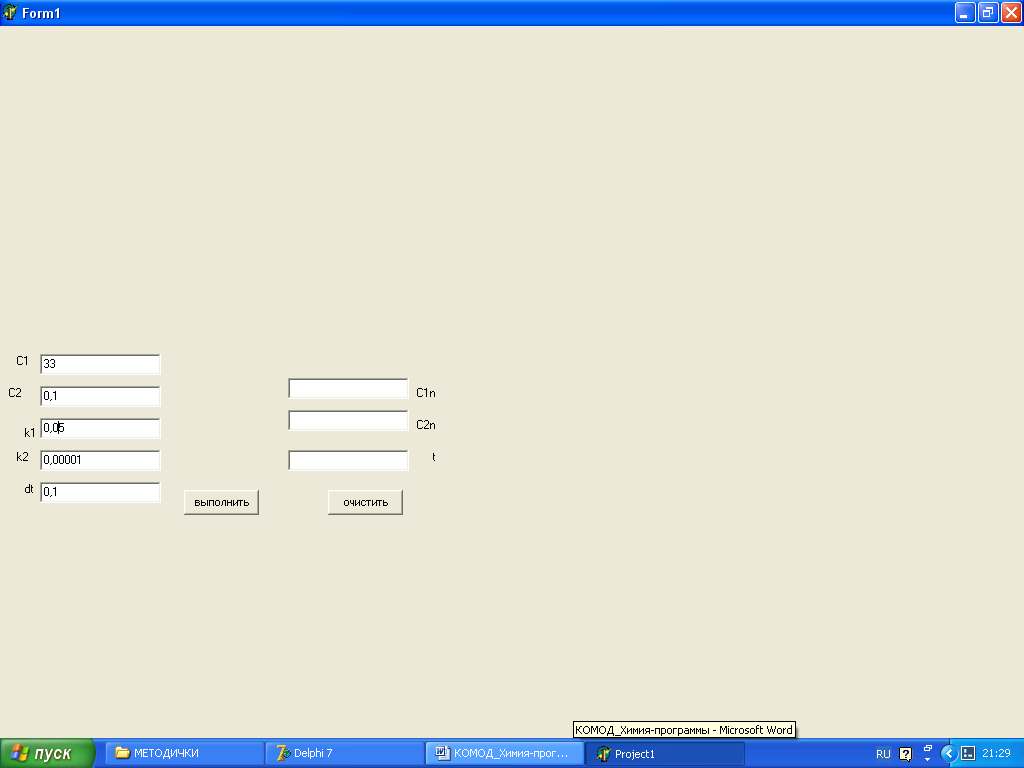
Рис. 4 Окно программы, ввод данных с клавиатуры.

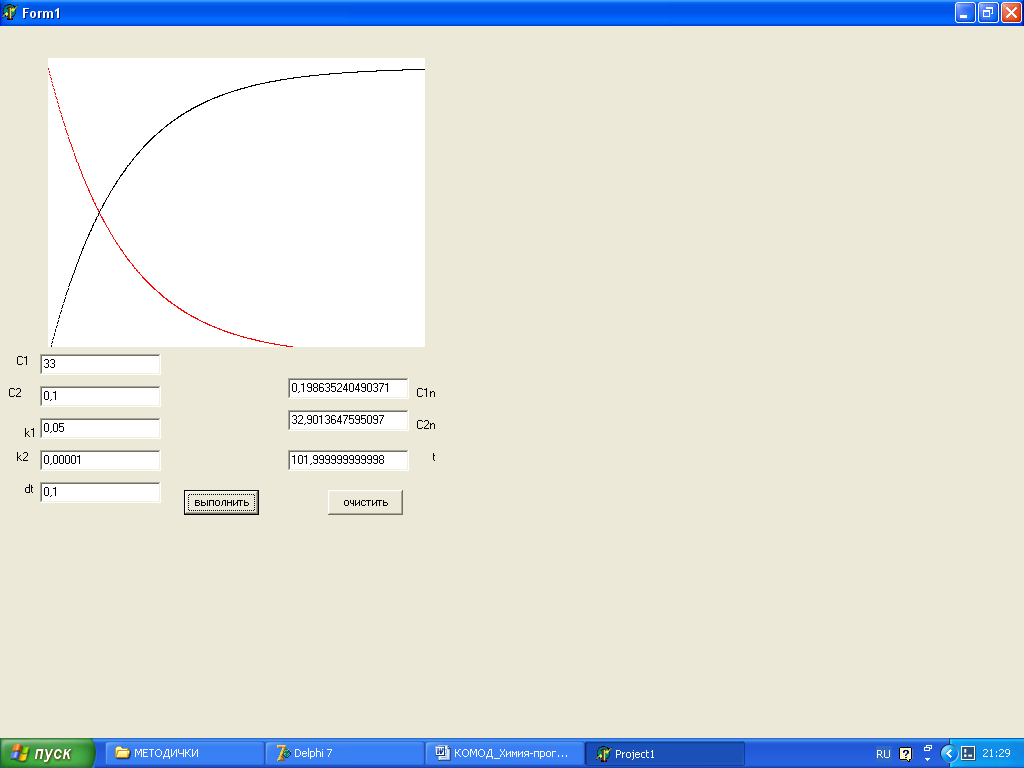
Рис. 5 Окно с результатами выполнения программы: вывод графиковC1(t), C2(t), конечных значений концентраций реагирующих веществ и времени реакции.

Данную задачу можно решить с использованием пакета Excel, что, конечно, значительно проще по сравнению с языками программирования. В соответствующий столбец записывается каждая из формул и средствами Excelпроизводится расчет (рис.6), а затем при помощи диаграммы выводится графики искомых зависимостей (рис.7).

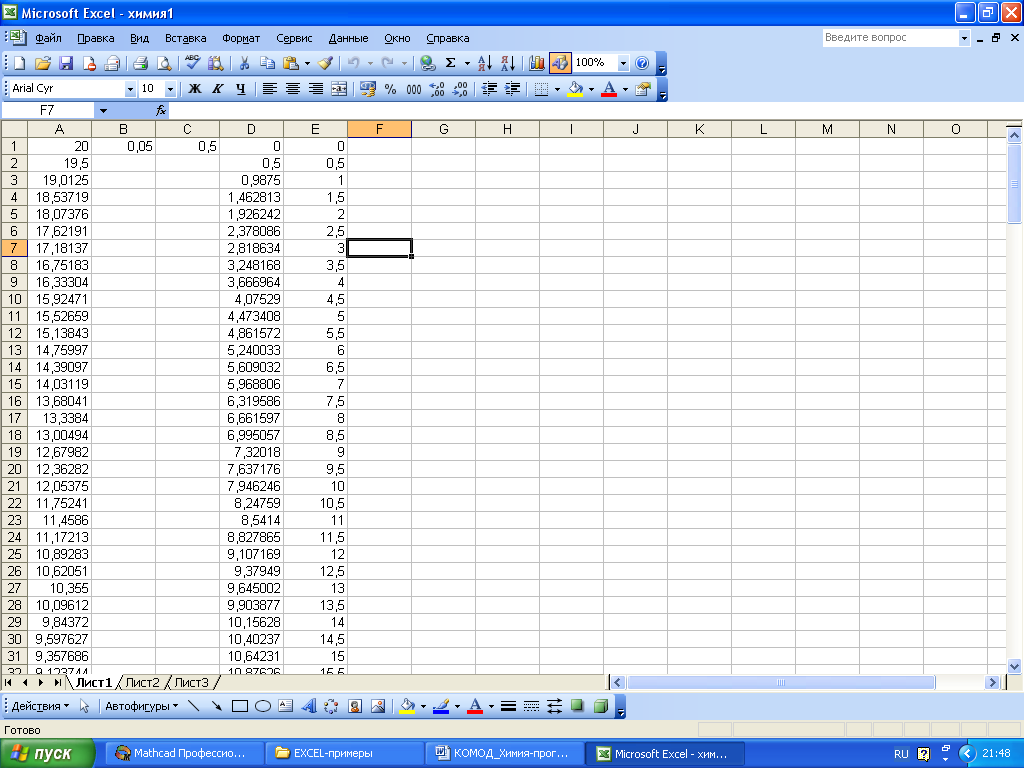
Рис. 6 Рабочее окно Excel, ввод данных

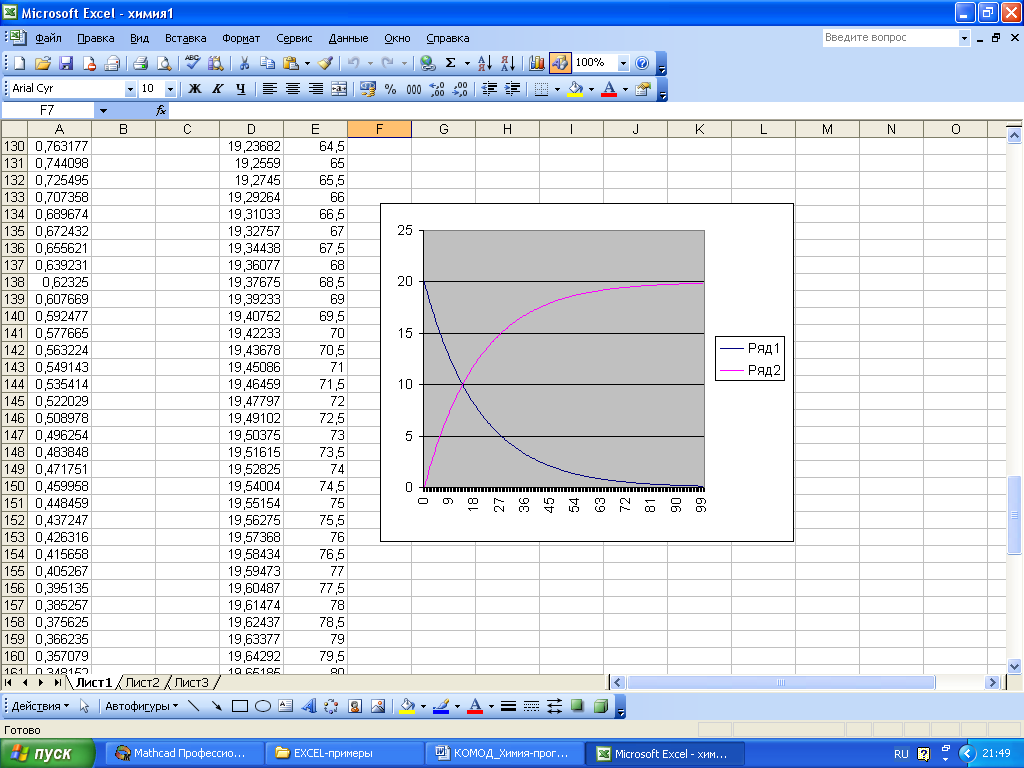
Рис. 7 Окно с результатами расчетов.

Для решения инженерных и естественнонаучных задач предназначен пакет прикладных программ Mathcad. Здесь не стоит целью подробно изучить Mathcad, а только показана возможность его применения для решения подобных задач. В файл записываются начальные данные и необходимые параметры, затем записываются все уравнения математической модели, выводятся поля вывода результатов расчетов и область графиков. При нажатии клавиши enter выполняется расчет, и, если нет ошибок в программе или данных, заполняются поля результатов (рис.8) и появляются графические зависимости (рис.9).

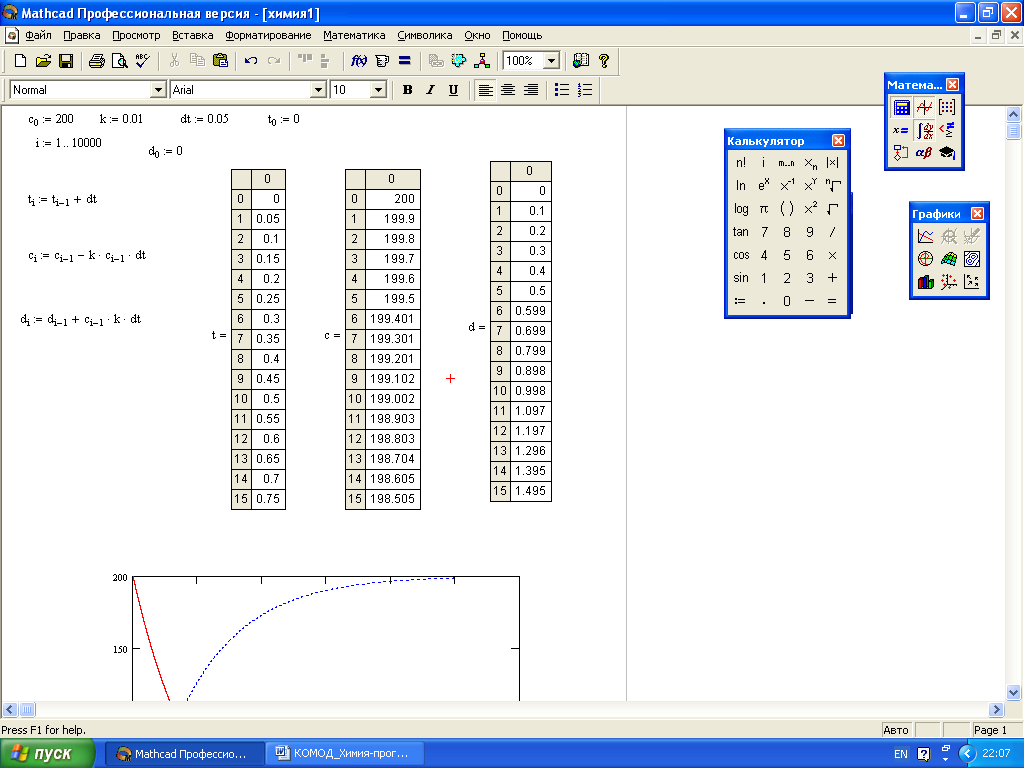
Рис. 8 Файл Mathcad с программой и результатами расчетов.

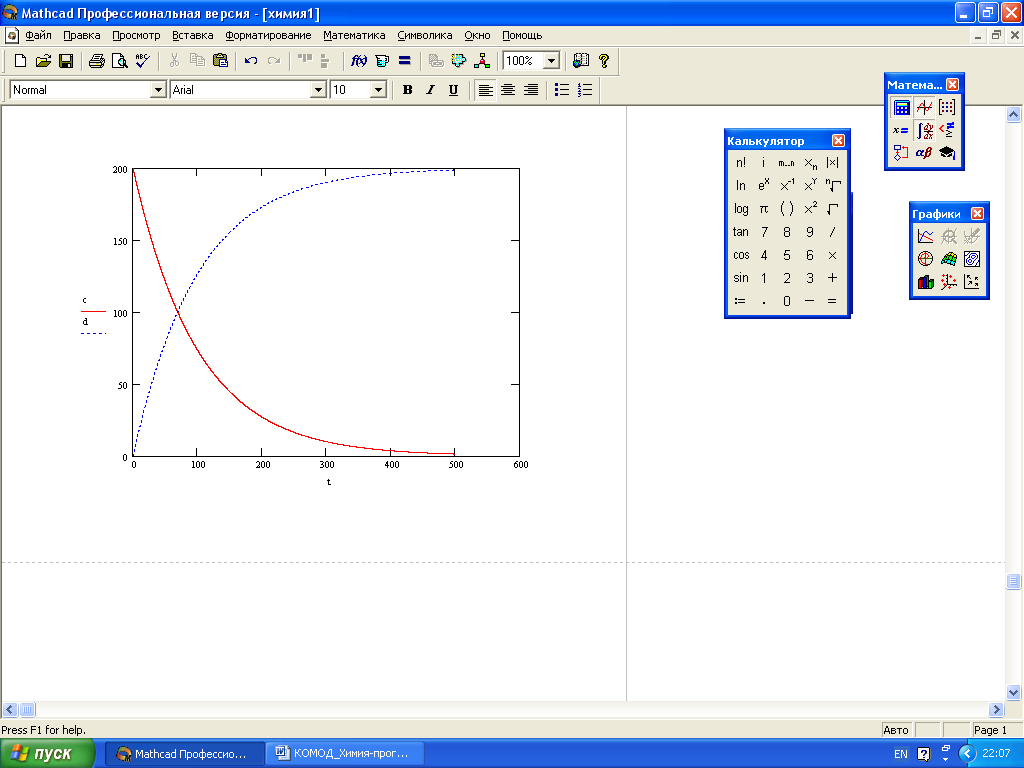
Рис. 9 Графические зависимости компонентов реакции во времени в пакете Mathcad.

Пример № 3

Составить модель реакции разложения первого порядка типа А  В + С, протекающей в адиабатическом режиме с тепловым эффектом, если известны: начальные концентрации и температура, тепловой эффект, теплоемкости реагентов, зависимость константы скорости реакции от температуры, приведенная ниже:

Т, ^оС ……50 55 60 65 70 72.5 78 84

к, ч^-1 ……1.4 1.6 2.2 3.0 4.0 4.7 7.2 9.4

Получить временные зависимости концентрации исходного компонента, концентраций продуктов реакции и температуры, построить зависимость скорости превращения реагента А от его концентрации в виде функции dC_A/dt = k(T)C_A(t). Математическое описание химической реакции с тепловым эффектом включает уравнение материального (кинетические) и теплового балансов. Кинетическое уравнение для исходного компонента реакции: . Уравнение теплового баланса при адиабатическом режиме имеет вид: , где c_V = (c_AC_A + c_BC_B + c_CC_C)V. Здесь с_V – объёмная теплоемкость системы, зависящая от текущих концентраций компонентов реакции, их теплоемкостей с_i и объема реакционной смеси V. В качестве упрощающего предположения допустим, что объемная теплоемкость с_V – величина постоянная, численно равная среднему значению теплоемкостей отдельных компонентов c_V = (c_A + c_B + c_C)/3. Окончательно дифференциальные уравнения балансов для данной реакции запишем в виде:

(А)

Искомые зависимости концентрации и температуры реакции от времени получают при интегрировании системы уравнений (А) (также д/б зависимость к от времени, полученная на машине). Если в процессе реакции выделяется тепло, которое (частично) отводится через стенку реактора при помощи хладагента, то при составлении уравнений математической модели, кроме уже приведенных исходных данных, необходимо знать: коэффициент теплоотдачи через стенку , поверхность теплообмена S, температуру хладагента Т_x. В этом случае дифференциальное уравнение скорости изменения температуры реакционной массы имеет вид:

(Б)

Скорость реакции описывается уравнением: (В). Уравнение (В) подставим в уравнение (Б)

(Г)

Совместное решение уравнений (Г) и (В) на машине позволяет изучить химическую реакцию, например, с выделением тепла при отводе избытка тепла. При этом можно варьировать S, , температуру хладагента Т_x.

Реакцию с тепловым эффектом иногда необходимо исследовать в условиях постоянной температуры. В этом случае тепло, выделяемое в ходе химической реакции, должно полностью отводиться через стенки реактора. При этом Т=const, следовательно, dT/dt=0, k(t)=const и уравнение (Г) можно преобразовать к виду:

.

С помощью этого уравнения можно найти закон программного изменения температуры хладагента, которое обеспечивает постоянство температуры реакционной массы. Здесь концентрация С_А – переменная величина, поэтому, чтобы равенство не нарушалось, температура Т_x должна изменяться по следующему закону: Теперь получаем закон изменения Т_x от времени при постоянной к.

Это задание сложнее предыдущих, т.к. имеются лишь экспериментальные данные изменения константы скорости от температуры. Есть два варианта решения задачи: можно, решая задачу, при каждом изменении температуры системы, сравнивать ее с экспериментальными данными и выбирать соответствующее значение константы скорости реакции. Второй способ – определить закон изменения константы скорости. Для этого в полулогарифмических координатах строится зависимость ln(ke[i])(1/te[i]) (она будет линейной), и по ней уже при помощи математи-ческого аппарата выводится уравнение для константы скорости реакции (procedureTForm1.Button2Click(Sender: TObject)).Далеепроизводитсямоделированиепоранееописаннойсхеме.

unitUnit1;

interface

uses

Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,

Dialogs, TeEngine, Series, StdCtrls, ExtCtrls, TeeProcs, Chart;

type

TForm1 = class(TForm)

Chart1: TChart;

Memo1: TMemo;

Label1: TLabel;

Button1: TButton;

Button2: TButton;

Edit1: TEdit;

Edit2: TEdit;

Label2: TLabel;

Label3: TLabel;

Memo2: TMemo;

Label4: TLabel;

Label5: TLabel;

Chart2: TChart;

Series3: TFastLineSeries;

Edit3: TEdit;

Label6: TLabel;

Edit4: TEdit;

Label7: TLabel;

Edit5: TEdit;

Label8: TLabel;

Memo3: TMemo;

Edit6: TEdit;

Label9: TLabel;

Label10: TLabel;

Chart3: TChart;

Series1: TFastLineSeries;

Series2: TFastLineSeries;

Series4: TFastLineSeries;

Edit7: TEdit;

Edit8: TEdit;

Label11: TLabel;

Label12: TLabel;

Label13: TLabel;

Label14: TLabel;

Label15: TLabel;

Series5: TFastLineSeries;

Series6: TFastLineSeries;

procedure FormCreate(Sender: TObject);{выводнаэкранэксперимен-тальныхданных}

procedure Button2Click(Sender: TObject); {выполнениепрограммы}

procedure Button1Click(Sender: TObject); {очисткаэкрана}

private

{ Private declarations }

public

{ Public declarations }

end;

var

Form1: TForm1;

i:integer;

Ea,k,k0,TT,dt,t,CA,CB,CC:real;

const

te:array [1..8] of real=(323,328,333,338,343,348,353,358);

ke:array [1..8] of real=(0.014,0.019,0.025,0.033,0.046,0.06,0.081,0.119);

R=8.31;

implementation

{$R *.dfm}

procedure TForm1.FormCreate(Sender: TObject);

begin

memo1.Clear;

for i:=1 to 8 do

memo1.Lines[0]:=memo1.Lines[0]+' '+floattostr(te[i]);

memo2.Clear;

for i:=1 to 8 do

memo2.Lines[0]:=memo2.Lines[0]+' '+floattostr(ke[i]);

memo3.Clear;

end;

procedure TForm1.Button2Click(Sender: TObject);

begin

CA:=strtofloat(edit1.Text);

dt:=strtofloat(edit2.Text);

t:=0;

for i:=1 to 8 do begin

chart3.series[0].AddXY(te[i],ke[i],'') ;

chart2.series[0].AddXY(1/te[i],ln(ke[i]),'') ;

end;

Ea:=(ln(ke[8])-ln(ke[1]))*R/(1/te[1]-1/te[8]);

edit3.Text:=floattostr(R);

edit5.Text:=floattostr(Ea);

k0:=ke[4]/exp(-Ea/(R*te[4]));

edit4.Text:=floattostr(k0);

TT:=strtofloat(edit6.Text);

Cb:=0; Cc:=0;

repeat

chart1.Series[0].AddXY(t,Ca,'');

chart1.Series[1].AddXY(t,Cb,'');

chart1.Series[2].AddXY(t,Cc,'');

ca:=ca-k0*exp(-Ea/(R*TT))*Ca*dt;

cb:=cb+k0*exp(-Ea/(R*TT))*Ca*dt;

cc:=cc+k0*exp(-Ea/(R*TT))*Ca*dt;

t:=t+dt;

tt:=tt+1;

memo3.Lines.Add(floattostr(Ca)) ;

edit7.Text:=floattostr(tt);

chart3.Series[1].AddXY(tt,k0*exp(-Ea/(R*TT)),'');

edit8.Text:= floattostr(t);

until Ca<0.0001;

end;

procedure TForm1.Button1Click(Sender: TObject);

begin

chart3.series[1].Clear;

chart1.Series[0].Clear;

chart1.Series[1].Clear;

chart1.Series[2].Clear;

edit1.Text:='';

edit2.Text:='';

edit6.Text:='';

edit7.Text:='';

edit8.Text:='';

memo3.Clear;

end;

end.

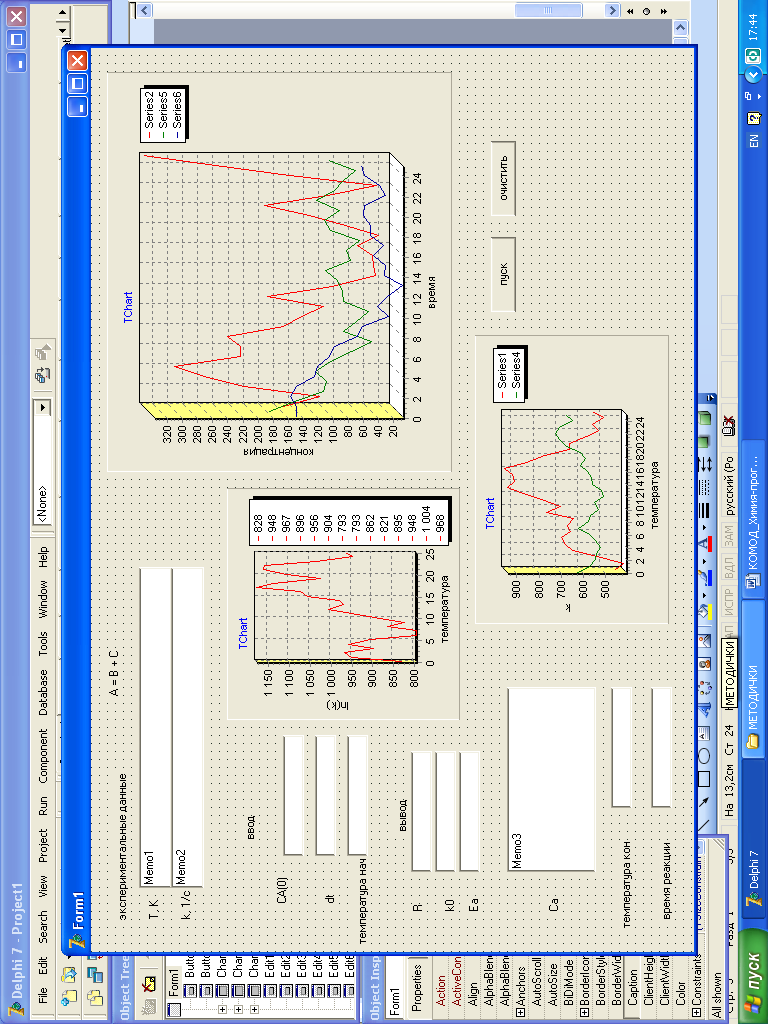
Рис. 10 Форма к примеру №3.

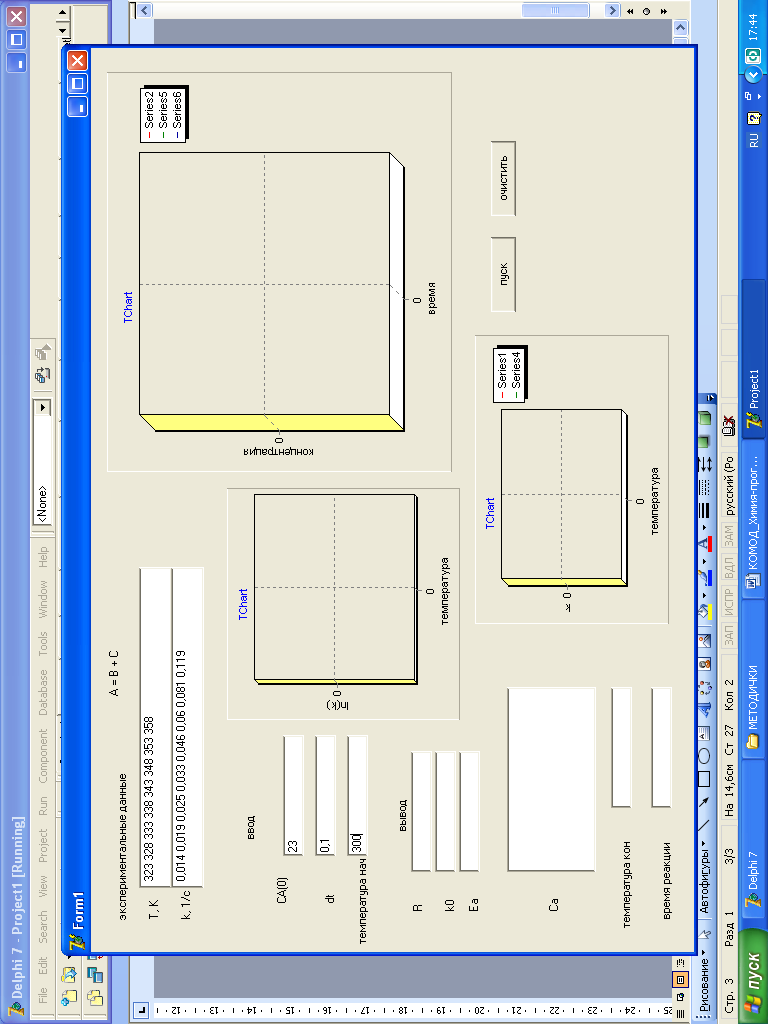
Рис. 11 Рабочее окно программы примера №3при запуске.

Рис. 12 Рабочее окно примера №3 после выполнения программы.

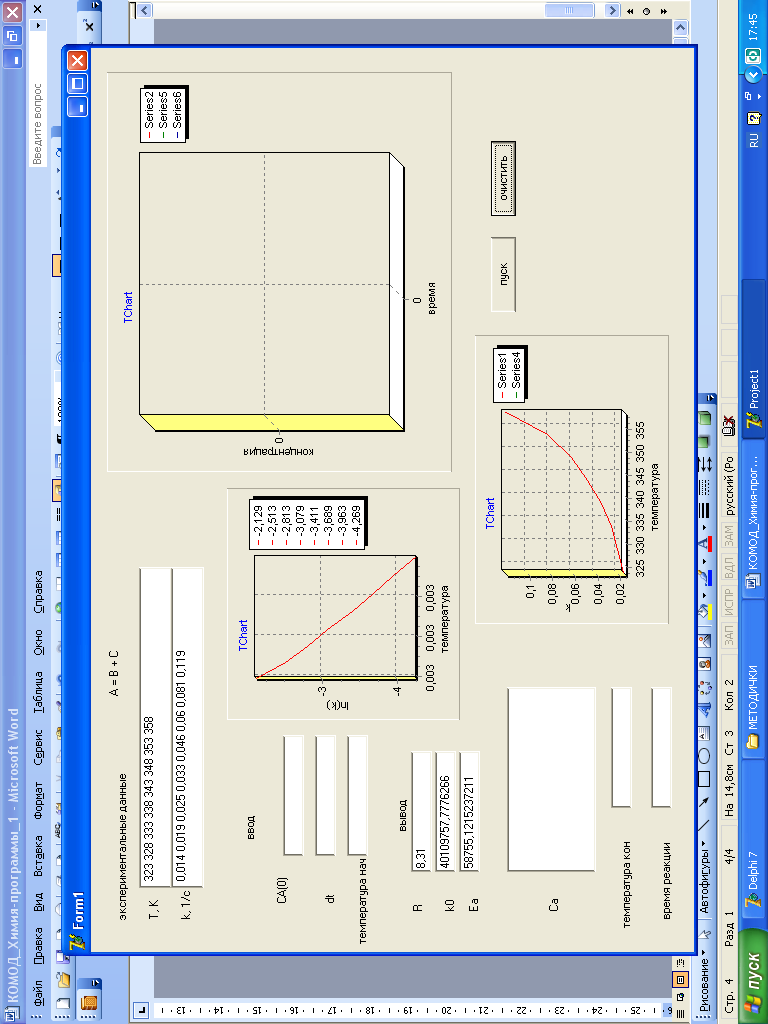
Рис. 13 Сброс результатов программы

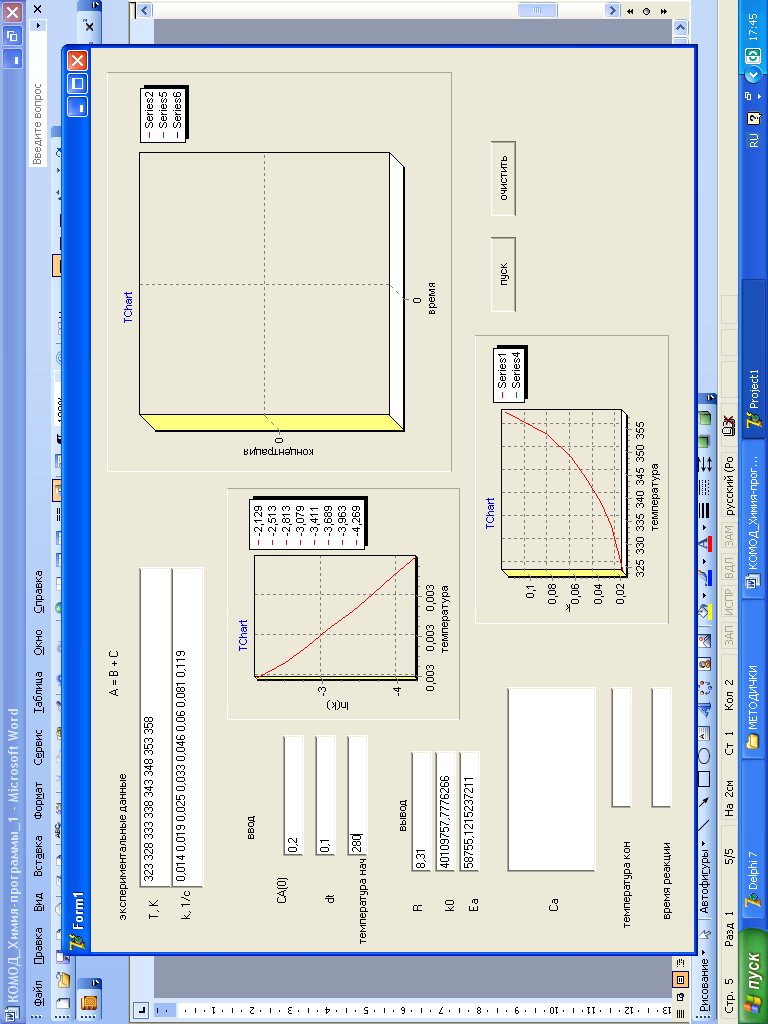
Рис. 14 Ввод новых данных

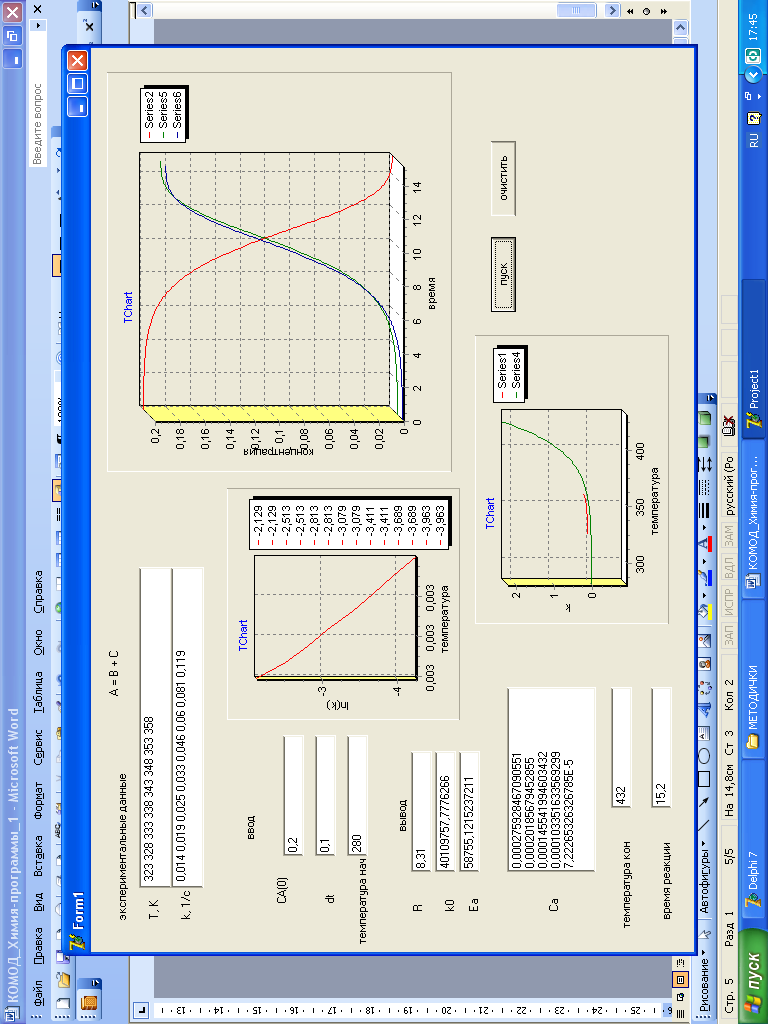
Рис. 15 Рабочее окно после выполнения программы

Пример № 4

 Составить заключение об адекватности математичес­кого описания, используя метод неявных функций и исходя из предположения, что скорость превращения исходного вещества А в продукт В при постоянной температуре описывается кинетическим уравнением реакции первого порядка (С). Экспериментальные данные по концентрации исходного компонента реагента равны:

t, C 0 10 20 30 40 50 60 70 80

C_Аэ, кмоль/м³ 1 0.6 0.39 0.240.15 0.10 0.06 0.03 0.015

В результате моделирования получаем зависимости k(t) и C_A(t). В интервале t₁  t  t₂ (t₁ = 0, t₂ = 70 c) коэффициент k=Const и, таким образом, модель адекватна реальному процессу. В интервале t₂ < t  t₃ (t₂=70 c, t₃=100 c) происходит изменение константы скорости. Вероятно, экспериментальные данные в этой области содержат значительные погрешности – область малых концентраций. Таким образом, в интервале t₁ t  t₂ уравнение (С) хорошо аппроксимирует опытные данные при k=0.45.

Очень распространенная задача построения зависимости или определения закона изменения параметров, в данном случае, концентрации реагирующих веществ, по экспериментальным данным. Такая зависимость позволяет впоследствии экстраполировать данные на другие условия эксперимента. Задача сводится к определению константы скорости реакции, построения экспериментальной и теоретической зависимостей, после чего делается вывод об адекватности полученной модели. Чтобы получить линейную зависимость выбираем координаты натуральный логарифм концентрации от времени. На форме имеется поле ввода номера экспериментальной точки (шага) для определения интервала расчета константы скорости (наиболее прямолинейный участок зависимости). Нижеприведенкодпрограммыиокнавыполненияпрограммы.

unit Unit1;

interface

uses

Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,

Dialogs, StdCtrls, ExtCtrls, TeeProcs, TeEngine, Chart, Series;

type

TForm1 = class(TForm)

Memo1: TMemo;

Chart1: TChart;

Button1: TButton;

Button2: TButton;

Button3: TButton;

Memo2: TMemo;

Label1: TLabel;

Label2: TLabel;

Edit1: TEdit;

Label3: TLabel;

Chart2: TChart;

Edit2: TEdit;

Label4: TLabel;

Series3: TFastLineSeries;

Edit3: TEdit;

Label5: TLabel;

Label6: TLabel;

Label7: TLabel;

Label8: TLabel;

Series1: TLineSeries;

Memo3: TMemo;

Series2: TLineSeries;

Memo4: TMemo;

procedure FormCreate(Sender: TObject);{выводнаэкранэксперимен-тальныхданных}

procedure Button3Click(Sender: TObject); {очисткатекстовыхполей}

procedure Button1Click(Sender: TObject); моделирование}

procedure Button2Click(Sender: TObject); {очисткаэкрана}

private

{ Private declarations }

public

{ Public declarations }

end;

var

Form1: TForm1;

var i,m:integer;

tt,cc:array [1..9] of real;

c:array [1..100000] of real;

t,dt,k:real;

implementation

{$R *.dfm}

procedure TForm1.FormCreate(Sender: TObject);

begin

memo1.Clear;

memo2.Clear;

memo3.Clear;

memo4.clear;

tt[1]:=0; cc[1]:=1000;

tt[2]:=10; cc[2]:=600;

tt[3]:=20; cc[3]:=390;

tt[4]:=30; cc[4]:=240;

tt[5]:=40; cc[5]:=150;

tt[6]:=50; cc[6]:=100;

tt[7]:=60; cc[7]:=60;

tt[8]:=70; cc[8]:=30;

tt[9]:=80; cc[9]:=15;

for i:=1 to 9 do begin

memo1.Lines[0]:=memo1.Lines[0]+' '+floattostr(tt[i]);

memo2.Lines[0]:=memo2.Lines[0]+' '+floattostr(cc[i]);

end;

i:=0;

while cc[i]>15 do begin

i:=i+1;

series1.AddXY(tt[i],(cc[i]),'');

series2.AddXY((tt[i]),ln(cc[i]),'');

end;

memo3.Lines[0]:='зеленая - расчет, красная - эксперимент';

memo4.Lines[0]:='ln(cc[i])';

end;

procedure TForm1.Button3Click(Sender: TObject);

begin

//memo1.Lines.Clear;

//memo2.Lines.Clear;

edit1.Text:='';

edit2.Text:='';

edit3.Text:='';

end;

procedure TForm1.Button1Click(Sender: TObject);

begin

i:=0;

while cc[i]>15 do begin

i:=i+1;

series1.AddXY(tt[i],(cc[i]),'');

series2.AddXY((tt[i]),ln(cc[i]),'');

end;

dt:=strtofloat(edit1.Text);

m:=strtoint(edit3.text);

k:=(ln(cc[1])-ln(cc[m]))/(ln(cc[1])*(tt[9]-tt[8]));

edit2.Text:=floattostr(k);

c[1]:=cc[1]; i:=1; t:=0;

while c[i]>0.001 do begin

series3.AddXY(t,c[i],'');

inc(i);

c[i]:=c[i-1]-k*c[i-1]*dt;

t:=t+dt;

end; end;

procedure TForm1.Button2Click(Sender: TObject);

begin

chart1.series[0].Clear;

chart1.Series[1].Clear;

chart2.Series[0].Clear;

end;

end.

Рис. 16 Форма примера № 4

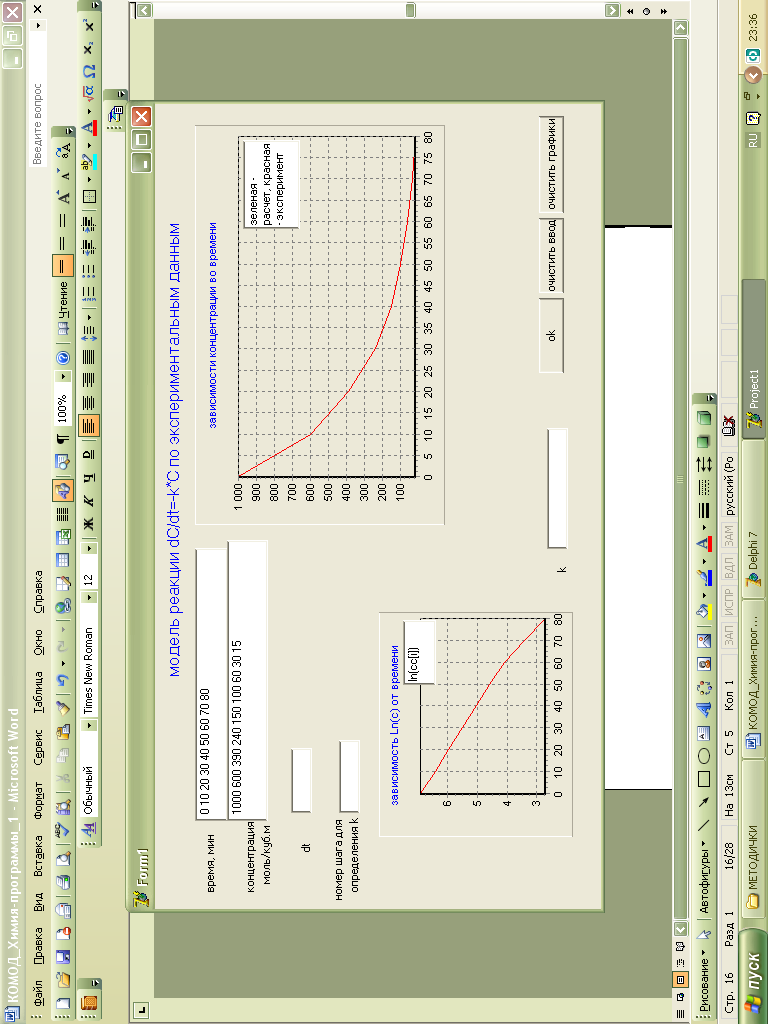
Рис. 17 Рабочее окно запуска программы

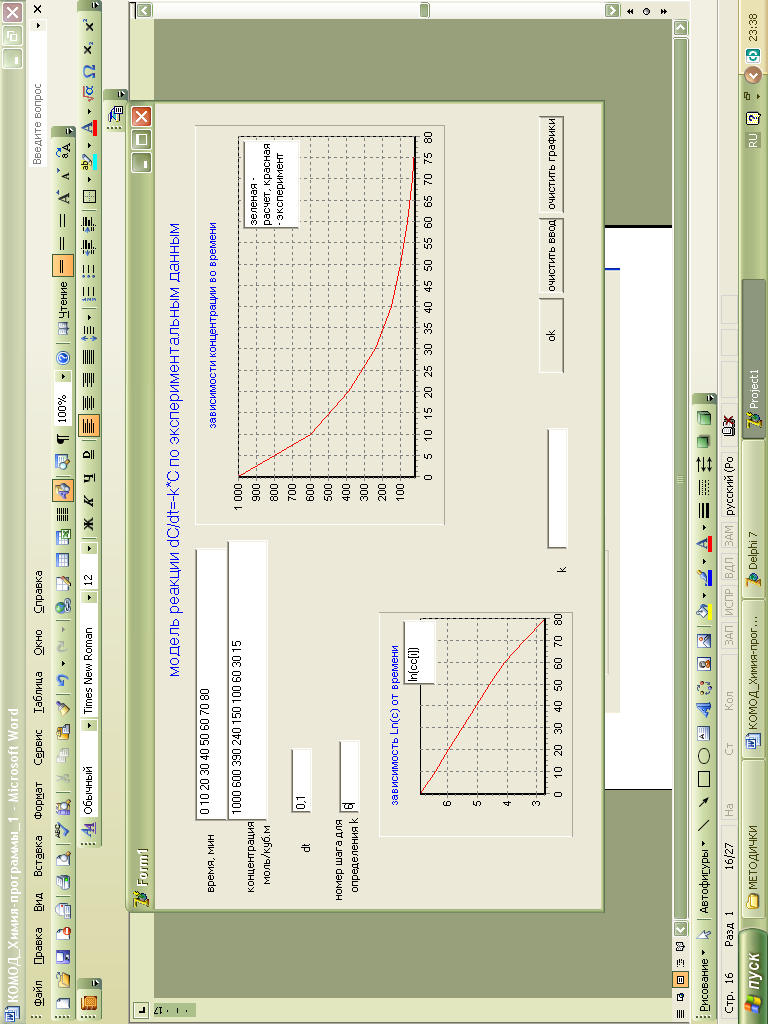
Рис. 18 Ввод данных

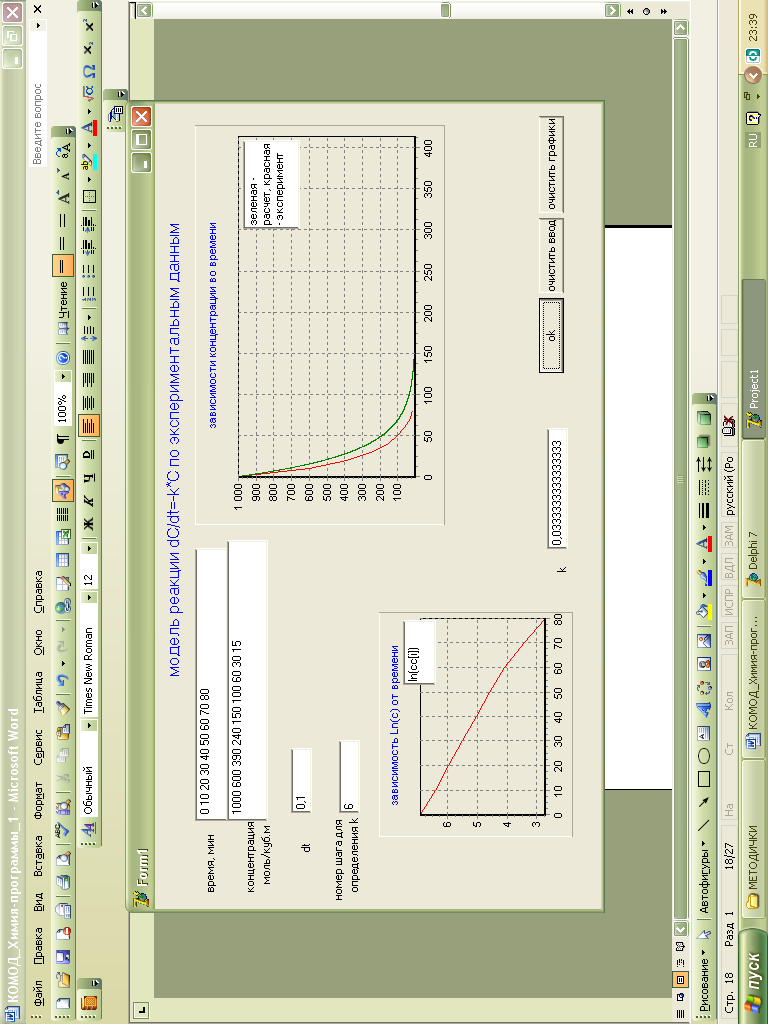
Рис. 19 Окно выполненной программы, красная зависимость – экспериментальная, зеленая - теоретическая

Аналогично предыдущей задаче, работу можно выполнить в пакете Mathcad. Модель решения та же самая, но исполнение – проще.

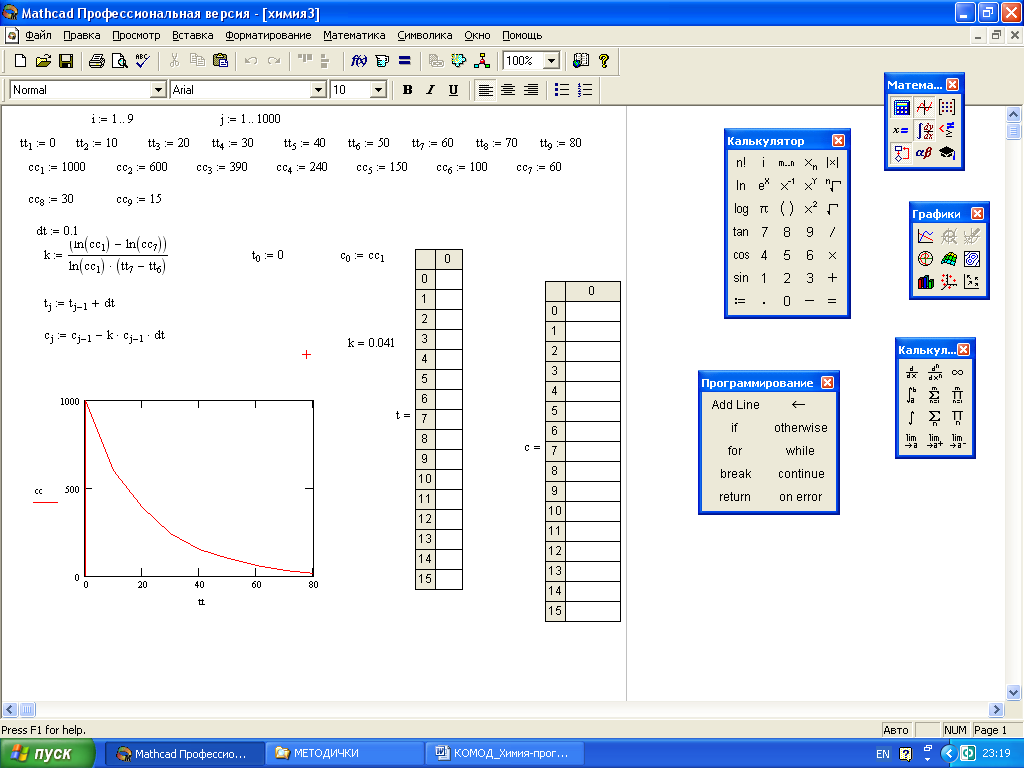
Рис. 20 Файл Mathcad с программой, исходными данными и теоретической зависимостью (ломанная кривая, т.е. – дискретная)

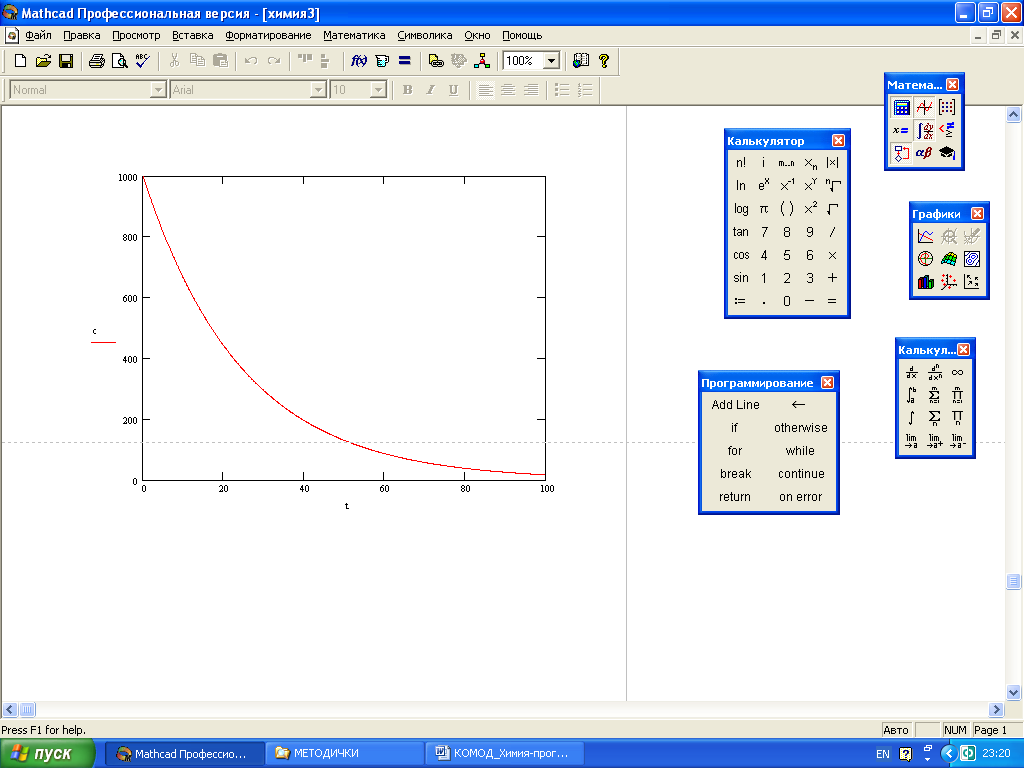
Рис. 21 Файл Mathcad с экспериментальной зависимостью (плавная кривая, без разрывов)

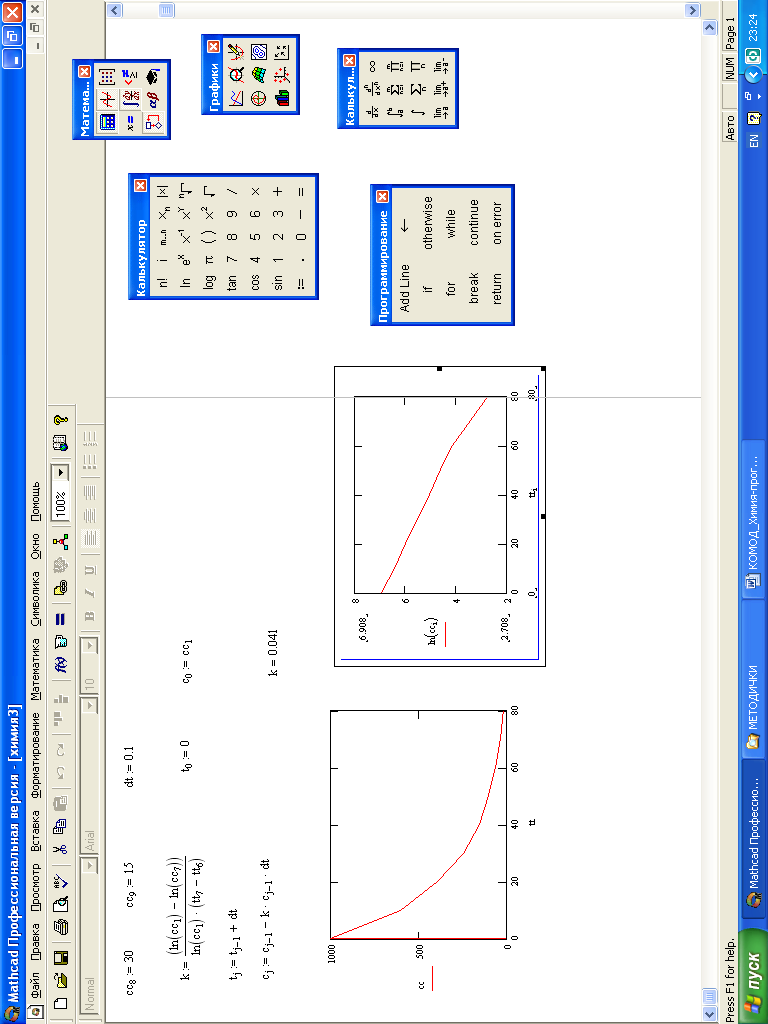
Рис. 22 Файл Mathcad с программой, исходными данными и теоретической зависимостью (ломанная кривая, т.е. – дискретная) зависимостью для определения k

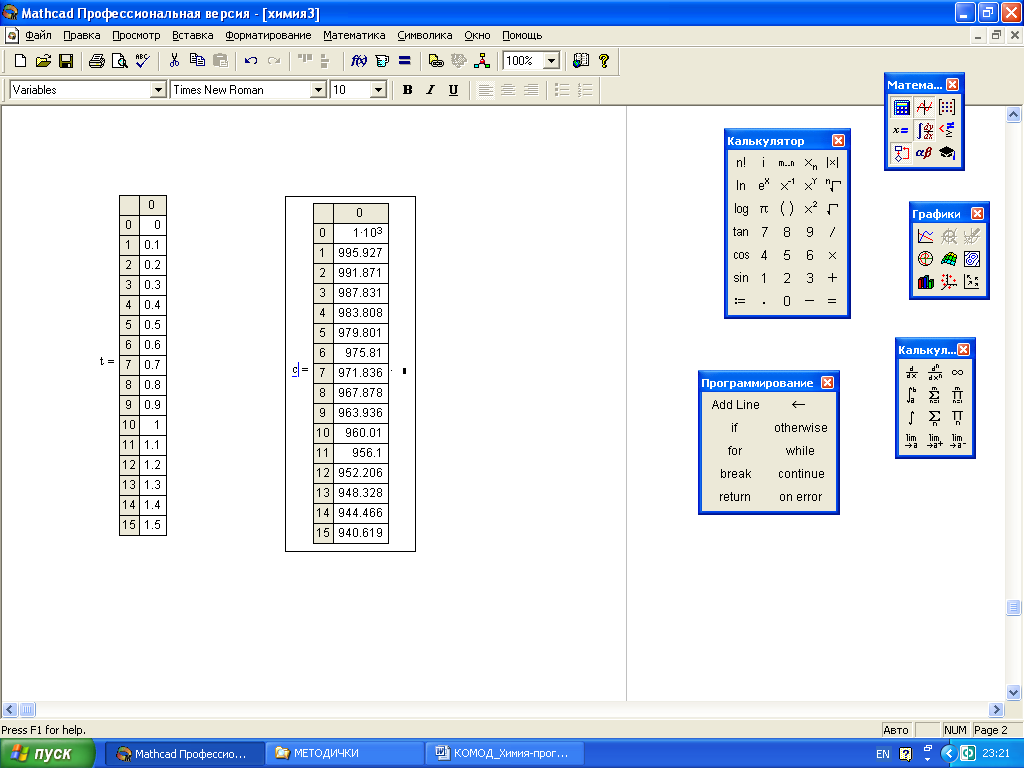
Рис. 23Файл Mathcad с данными расчетов

Аналогично предыдущей задаче, моделировать химическую реакцию можно и в excel. Ниже приводятся соответствующие рисунки.

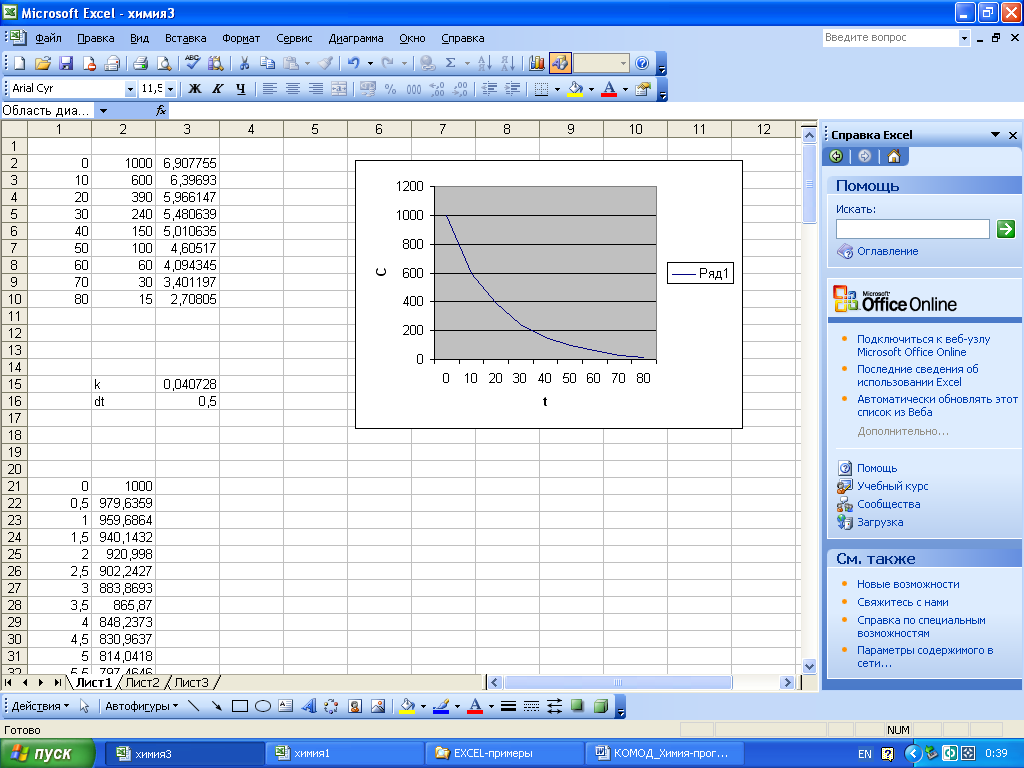
Рис. 24 Файл Excel с исходными данными и экспериментальной зависимостью

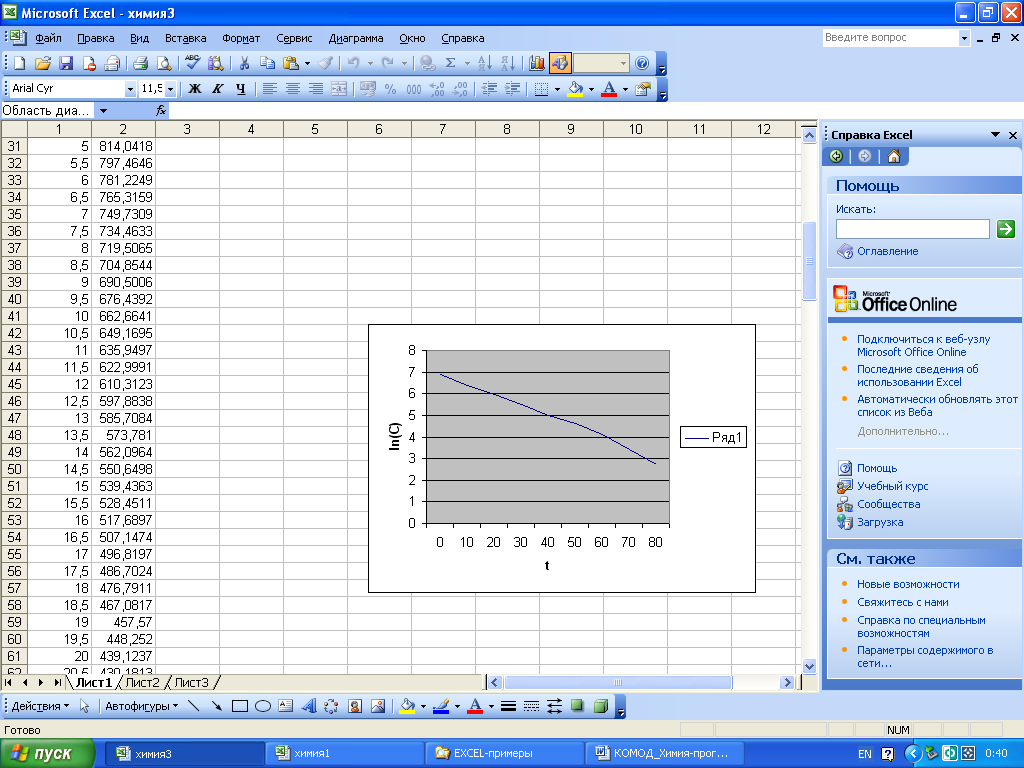
Рис. 25Файл Excel с исходными данными и экспериментальной зависимостью для определения k

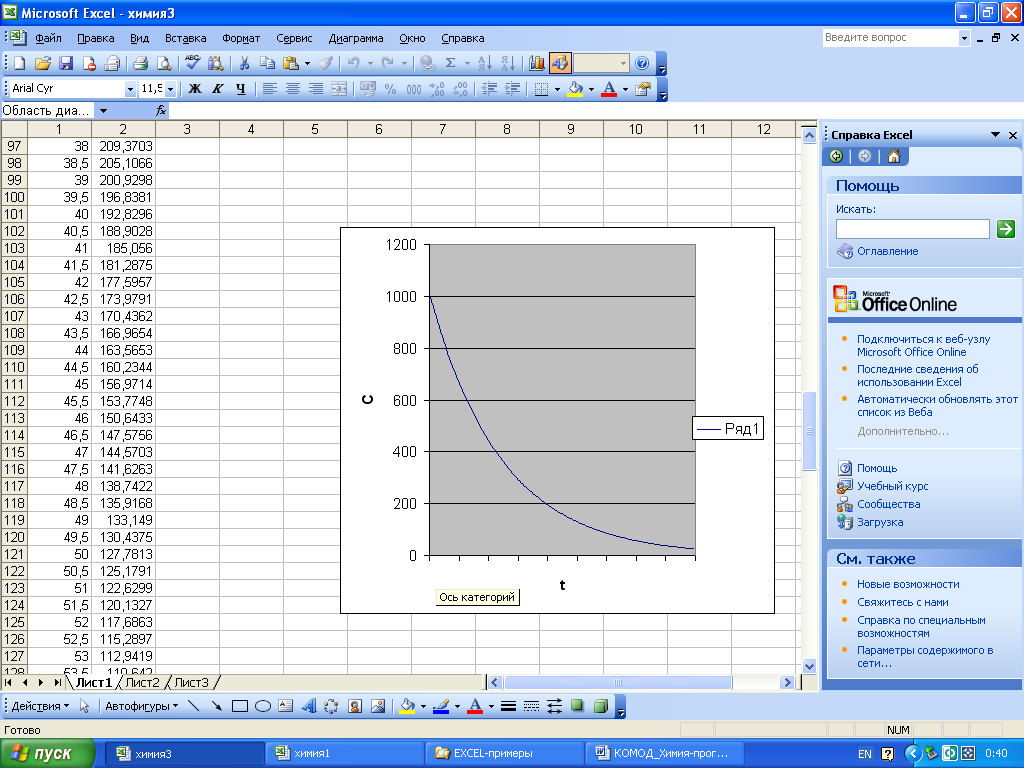
Рис. 26Файл Excel с исходными данными и теоретической зависимостью

Пример №5

 В ходе изучения термического разложения динитроксида на золоте при 990^оС получены следующие кинетические данные:

время, мин 30 53 100

степень превращения, % 32 50 73

Определить порядок реакции n и константу скорости k с помощью вычислительной машины. Для решения задачи надо подготовить четыре вычислительных блока: блок, моделирующий собственно химическую реакцию, блок, воспроизводящий экспериментальную кривую,

В уравнении (Т) производим замену: С = С₀(1-x), где С₀ – начальная концентрация. Получаем: (Т*). Для вычисления степени превращения x необходим дополнительный сумматор: - (-x = (1-x) – 1). ( константа скорости реакции должна получиться 2.110^-4 с^-1.

Задание аналогично предыдущему, подробно не рассматривается, имеются код программы и различные этапы ее выполнения.

unit Unit1;

interface

uses

Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,

Dialogs, StdCtrls,Math, ExtCtrls, TeeProcs, TeEngine, Chart, Series;

type

TForm1 = class(TForm)

Memo1: TMemo;

Chart1: TChart;

Edit1: TEdit;

Label1: TLabel;

Label2: TLabel;

Label3: TLabel;

Label4: TLabel;

Label5: TLabel;

Button1: TButton;

Button2: TButton;

Button3: TButton;

Chart2: TChart;

Edit2: TEdit;

Label6: TLabel;

Series2: TFastLineSeries;

Edit3: TEdit;

Label7: TLabel;

Edit4: TEdit;

Label8: TLabel;

Memo2: TMemo;

Series4: TFastLineSeries;

Memo3: TMemo;

Memo4: TMemo;

Series3: TLineSeries;

Series1: TLineSeries;

procedureFormCreate(Sender: TObject); {вывод на экран экперимен-тальных данных и построение полулогарифмической зависимости}

procedure Button2Click(Sender: TObject); {очисткатекстовыхполей}

procedure Button3Click(Sender: TObject); {очисткаграфиков}

procedure Button1Click(Sender: TObject); {основнаяпрограмма}

private

{ Private declarations }

public

{ Public declarations }

end;

var

Form1: TForm1;

i:integer;

tt,al:array [0..3] of real;

k,dt,t,c,n:real;

implementation

{$R *.dfm}

procedure TForm1.FormCreate(Sender: TObject);

begin

tt[0]:=0; al[0]:=0;

tt[1]:=30; al[1]:=0.32;

tt[2]:=53; al[2]:=0.5;

tt[3]:=100; al[3]:=0.73;

memo1.Clear;

memo2.Clear;

memo3.Clear;

memo4.Clear;

for i:=0 to 3 do begin

memo1.Lines[0]:=memo1.Lines[0]+' '+floattostr(tt[i]);

memo2.Lines[0]:=memo2.Lines[0]+' '+floattostr(al[i]);

series1.AddXY(tt[i],1-al[i],'');

series2.AddXY(tt[i],Ln(1-al[i]),'')

end;

k:= abs(ln(1-al[3])-ln(1-al[1]))/(tt[3]-tt[1]);

edit2.Text:=floattostr(k);

n:=100*(ln(al[3])-ln(al[1]))/((ln((1-al[1])/(1-al[3])))*(tt[3]-tt[1]));

//n:=(ln((1-al[1])/(1-al[3]))+(ln(tt[1]/tt[3])))/(ln((1-al[3])/(1-al[1])));

edit3.Text:=floattostr(n);

memo3.Lines[0]:='зеленая - эксперимент, красная - расчет';

memo4.Lines[0]:='зеленая -Ln(1-al[i]), красная - 1-al[i] ';

end;

procedure TForm1.Button2Click(Sender: TObject);

begin

edit1.Text:='';

edit4.text:='';

end;

procedure TForm1.Button3Click(Sender: TObject);

begin

series3.Clear;

series4.Clear;

end;

procedure TForm1.Button1Click(Sender: TObject);

begin

c:=strtofloat(edit1.text);

dt:=strtofloat(edit4.text);

t:=0;

while c>0.001 do begin

series3.AddXY(t,c,'');

t:=t+dt;

c:=c-k*power(c,n)*dt;

end;

c:=strtofloat(edit1.text);

for i:=0 to 3 do

series4.AddXY(tt[i],c*(1-al[i]),'');

end;

end.

Рис. 27 Исходная форма.

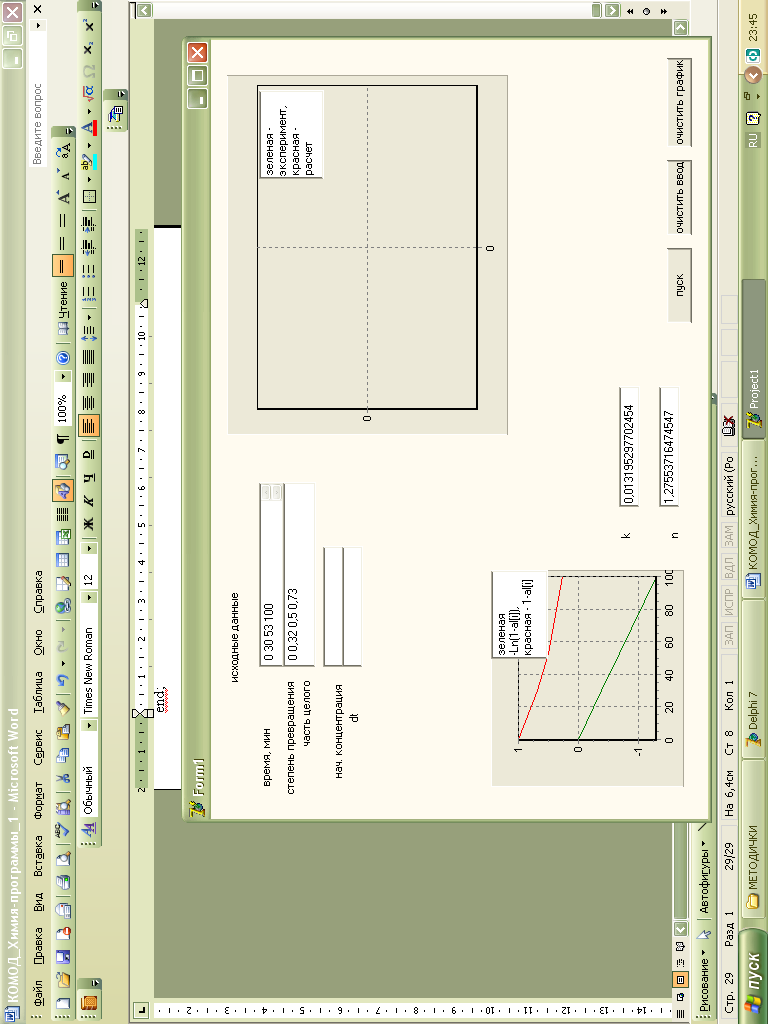
Рис. 28 Окно программы с расчетом константы скорости (k) и порядка реакции (n)

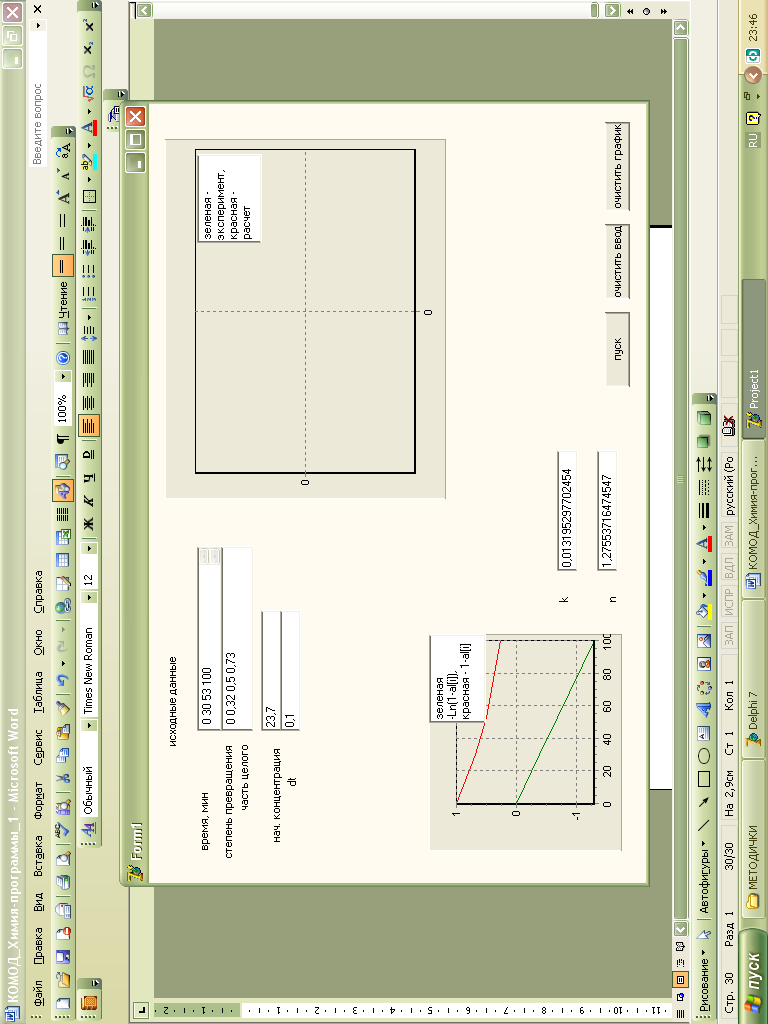
Рис. 29 Окно программы, ввод данных с клавиаткры

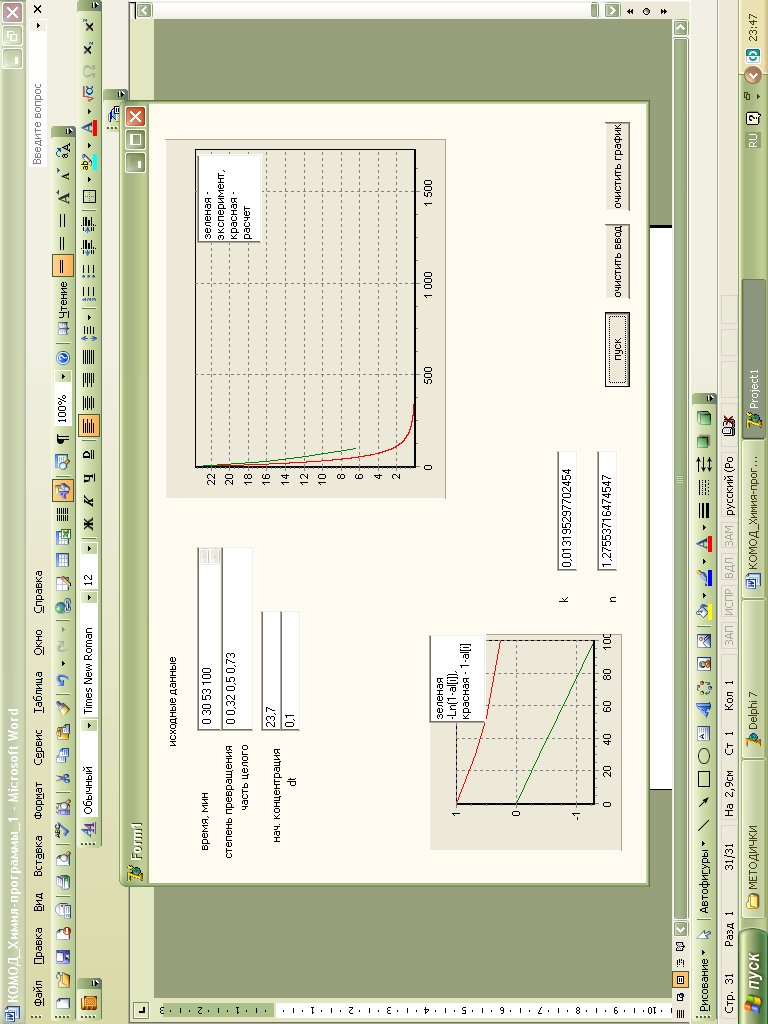
Рис. 30 Рабочее окно с экспериментальной и теоретической зависимостями.

Рис. 31 Рабочее окно, ввод новых данных

Рис. 32Рабочее окно с экспериментальной и теоретической зависимостями.