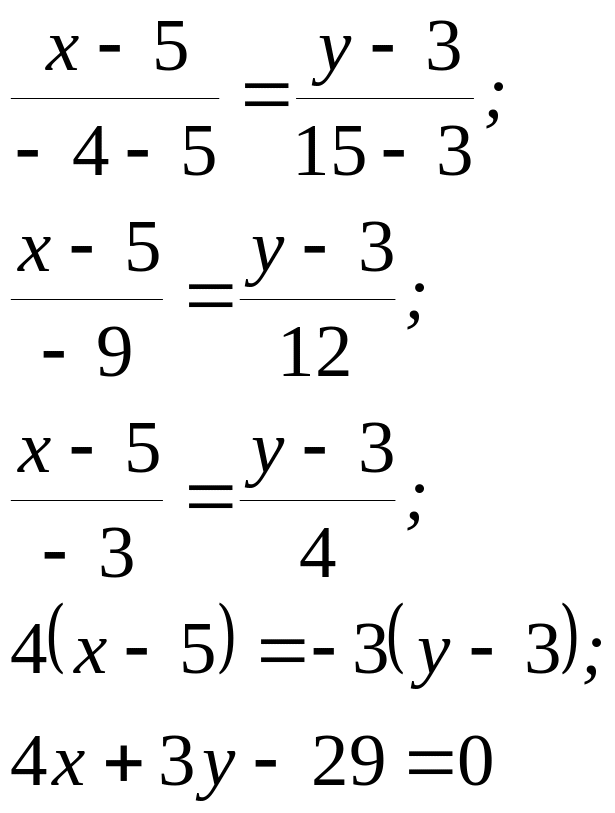Аналитическая геометрия на плоскости._______________________________________
Задача 1
Даны вершины А(5; 3), В(-11; -9), С(-4; 15) треугольника АВС. Требуется найти:
уравнения сторон треугольника АВ, АС и ВС;
уравнения высот АL, BH и СK;
длины высот;
величины углов (в градусах, минутах и радианах);
уравнение биссектрисы BS;
уравнение медианы СМ.
Решение:
Найдём уравнения сторон:
Уравнение стороны
AВ
или уравнение прямой проходящей через
точки A(xA;
yA)
и В(xB;
yB),
имеет вид:
Подставив в эту формулу координаты точек A и B, получаем:
3х-4у-3=0 – общее уравнение прямой (стороны) AB.
у= – уравнение прямой (стороны) AB с угловым коэффициентом.
|
Уравнение стороны
AС
или уравнение прямой проходящей через
точки A(xA;
yA)
и С(xC;
yC),
имеет вид:
Подставив в эту формулу координаты точек A и С, получаем:
4х+3у-29=0 – общее уравнение прямой (стороны) AС.
у= – уравнение прямой (стороны) AС с угловым коэффициентом.
|
Уравнение стороны
BС
или уравнение прямой проходящей через
точки В(xB;
yB)
и С(xC;
yC),
имеет вид:
Подставив в эту формулу координаты точек B и С, получаем:
24х-7у+201=0 – общее уравнение прямой (стороны) BС.
у= – уравнение прямой (стороны) BС с угловым коэффициентом.
|
Найдём уравнения высот:
определим сначала угловые коэффициенты высот:
ALBС kAL·kBC=-1
|
ВHAС kBH·kAC=-1
|
|
найдём уравнения высот:
найдём уравнение высоты AL, как уравнение прямой, проходящей через точку A(xA; yA) в заданном угловым коэффициентом kAL направлении: у-уА=kАL(х-хА)
7х+24у-107=0 – общее уравнение прямой (высоты) AL.
|
найдём уравнение высоты BH, как уравнение прямой, проходящей через точку B(xB; yB) в заданном угловым коэффициентом kBH направлении: у-уB=kBH(х-хB)
3х-4у-3=0 – общее уравнение прямой (высоты) BH. |
найдём уравнение высоты CK, как уравнение прямой, проходящей через точку _______ в заданном угловым коэффициентом ____ направлении:
____________ – общее уравнение прямой (высоты) CK.
|
Найдём длины высот:
I способ:
Нахождение расстояния от точки до прямой
Пусть заданы прямая l: Ах+Ву+С=0, и точка М(х0; у0), тогда расстояние d от точки М до прямой l находится по формуле:
![]()
найдём |AL|, как расстояние от точки A(5; 3) до прямой ВС: 24х-7у+201=0
|
найдём |BH|, как расстояние от точки B(-11; -9) до прямой AС: 4х+3у-29=0
|
найдём |CK|, как расстояние от точки C(-4; 15) до прямой AB: 3х-4у-3=0
|