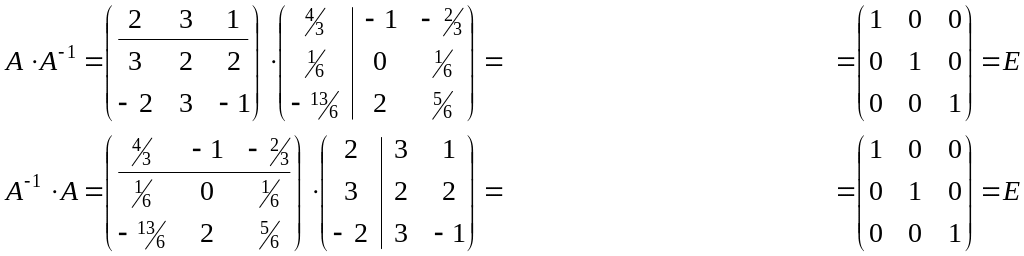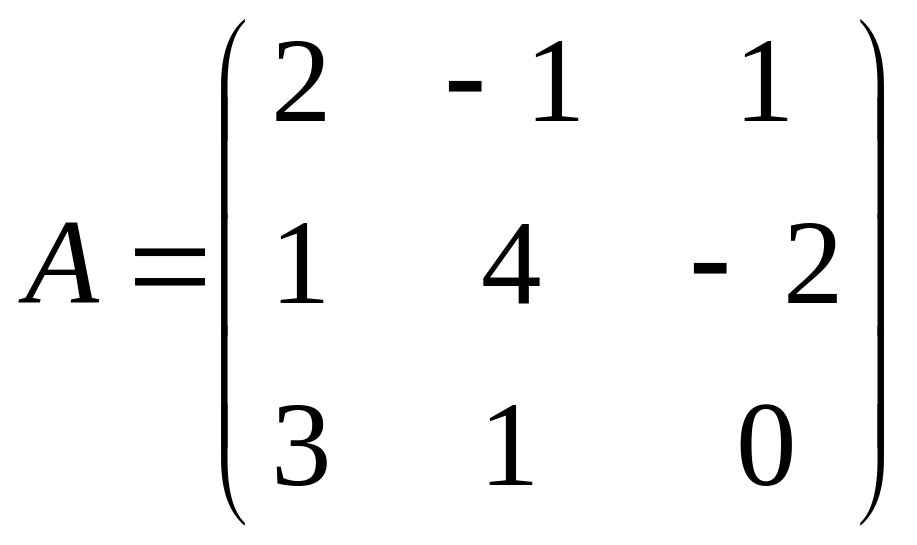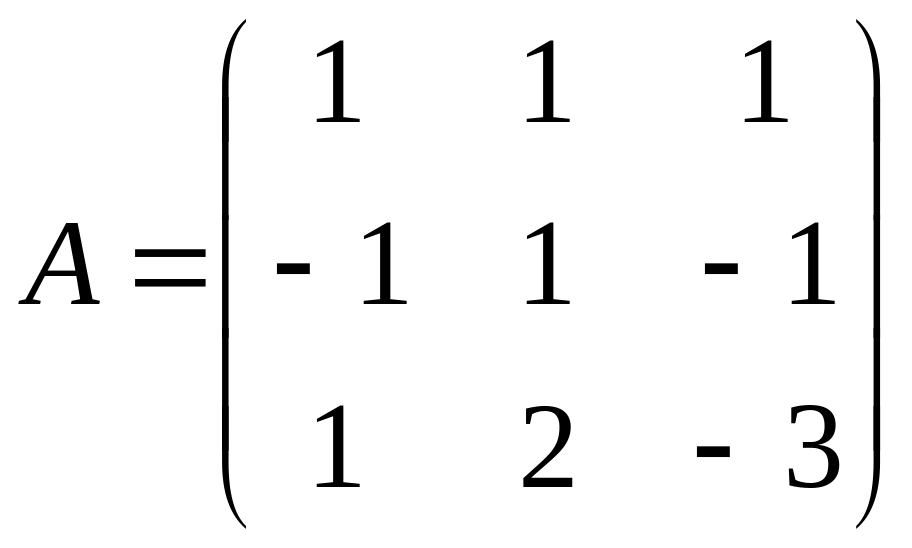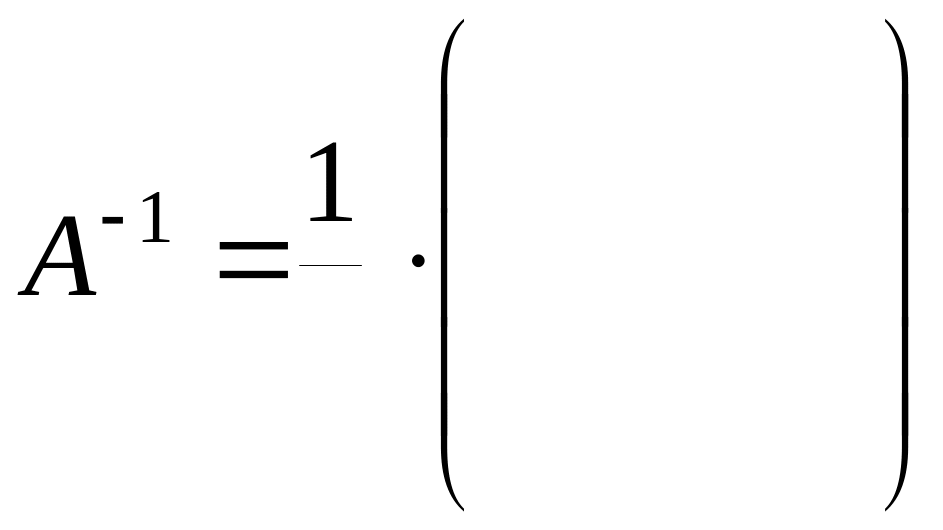Обратная матрица. Ранг матрицы.___________________________________________________

Обратная матрица

Матрица А^-1 называется обратной по отношению к квадратной матрице А, если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица:

А·А^-1=А^-1·А=Е.

Для существования матрицы А^-1 необходимым и достаточным условием является требование |А|0.

Если определитель матрицы отличен от нуля (|А|0), то такая квадратная матрица называется невырожденной, или неособенной; в противном случае (при |А|=0) — вырожденной, или особенной.

1. Укажите, какие из матриц имеют обратные, а также выделите невырожденные (неособенные) и вырожденные (особенные) матрицы:

вывод:  невырожденные матрицы (неособенные): вырожденные матрицы (особенные):

вывод:  невырожденные матрицы (неособенные): вырожденные матрицы (особенные):

Теорема (необходимое и достаточное условие, существования обратной матрицы). Обратная матрица А^-1 существует (и единственна) тогда и только тогда, когда исходная матрица невырожденная.

Обратную матрицу можно найти с помощью элементарных преобразований:

по следующему алгоритму:

1. выпишем заданную квадратную матрицу А и припишем ей справа соответственную единичную матрицу Е;

2. с помощью элементарных преобразований получим слева вместо матрицы А единичную Е:

• получим значение первого диагонального элемента а₁₁=1, при этом можно строки менять местами (полностью), умножать на любое, отличное от нуля число, и складывать поэлементно;

• получим значения а_i1=0, 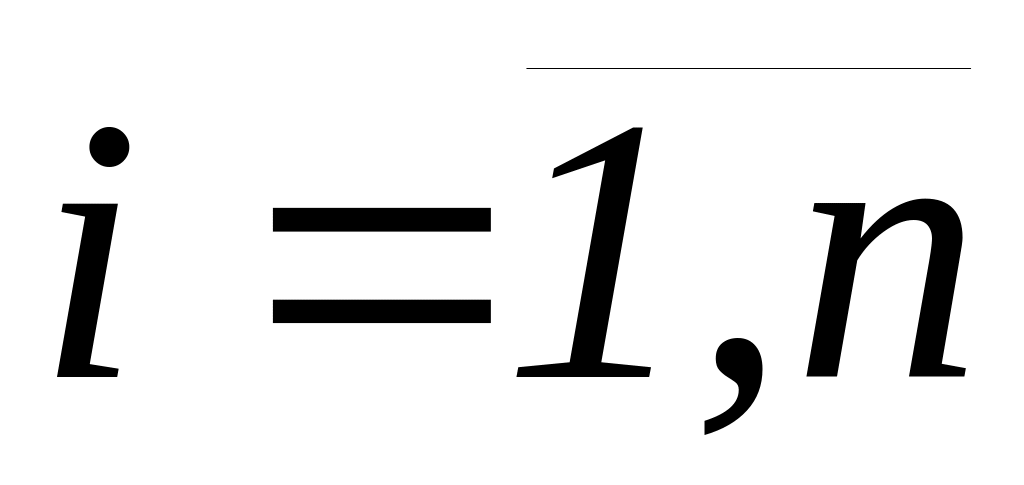, где i1, то есть добьёмся, чтобы все остальные элементы первого столбца стали равными нулю;

• далее аналогично, получим значение второго диагонального элемента а₂₂=1, и добьёмся, чтобы все остальные элементы второго столбца стали равными нулю а_i2=0, , где i2;

• далее аналогично, будем получать значение диагонального элемента равное 1, и всех остальных элементов этого столбца равными нулю

3. тогда при соответствующих элементарных преобразованиях матрица Е превратится в А^-1.

А/Е Е/А-1

2. Найти обратную матрицу с помощью присоединенной единичной и элементарных преобразований и выполнить проверку правильности её нахождения:

, следовательно, обратная матрица существует. Проверка: А·А-1=А-1·А=Е

, следовательно, обратная матрица существует. Проверка: А·А-1=А-1·А=Е

3. Найти обратную матрицу с помощью присоединённой единичной и элементарных преобразований и выполнить проверку правильности её нахождения:

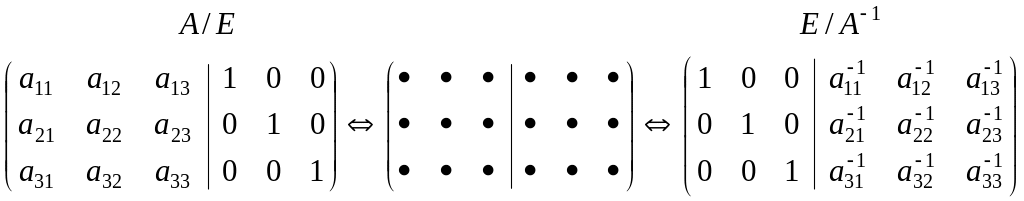
, следовательно, обратная матрица существует. Проверка: А·А-1=А-1·А=Е

следовательно, обратная матрица существует. Проверка: А·А-1=А-1·А=Е

Обратную матрицу можно найти с помощью определителя и алгебраических дополнений:

например, для матрицы второго порядка А ищем А^-1 – обратную матрицу (если она существует) по формуле:

4. Найти обратную матрицу с помощью определителя и алгебраических дополнений:

 А-1. получили, что Итак,	 А-1. получили, что Итак,
 А-1. получили, что Итак,	 А-1. получили, что Итак,

например, для матрицы третьего порядка А ищем А^-1 – обратную матрицу (если она существует) по формуле:

5. Найти обратную матрицу с помощью определителя и алгебраических дополнений:

Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы. Ранг матрицы А обозначается rangА, или r(А).

Из определения следует: