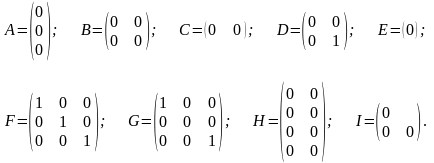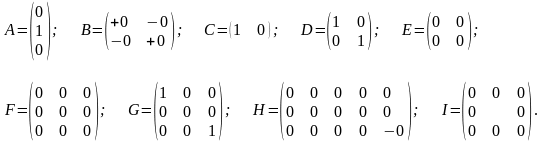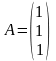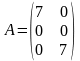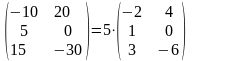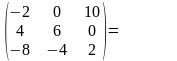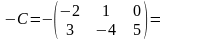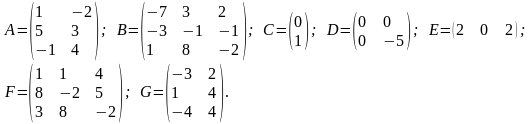12. Укажите нулевые матрицы:

нулевые матрицы:

нулевые матрицы:

Квадратная матрица называется симметрической, если а_ij=а_ji.

13. Укажите вид матрицы:

Пример матрицы	Вид матрицы	Пример матрицы	Вид матрицы

Действия над матрицами

Умножение матрицы на число: Произведением матрицы А на число  называется матрица В=А, элементы которой b_ij=а_ij, для

Общий множитель всех элементов матрицы можно выносить за знак матрицы.

14. Выполните действия:

Вычислить:	Вынести общий множитель:
Вычислить:	Вынести общий множитель:
Вычислить:	Вынести общий множитель:

Операции сложения и вычитания матриц выполняются только для матриц одинаковых размеров (порядков):

Сложение матриц: Суммой двух матриц А и В одинакового размера тп называется матрица С=А+В, элементы которой с_ij=а_ij+b_ij, для (т.е. матрицы складываются поэлементно).

Вычитание матриц: Разность двух матриц одинакового размера определяется через предыдущие операции: А-В=А+(-1)·В.

15. Выясните возможно ли выполнить сложение или вычитание матриц и вычислите сумму и разность матриц (если возможно):

АА= АВ= АС= АD= АE= АF= АG=	ВА= ВВ= ВС= ВD= ВE= ВF= ВG=	СА= СВ= СС= СD= СE= СF= СG=	DА= DВ= DС= DD= DE= DF= DG=	EА= EВ= EС= ED= EE= EF= EG=	FА= FВ= FС= FD= FE= FF= FG=	GА= GВ= GС= GD= GE= GF= GG=
АА= АВ= АС= АD= АE= АF= АG=	ВА= ВВ= ВС= ВD= ВE= ВF= ВG=	СА= СВ= СС= СD= СE= СF= СG=	DА= DВ= DС= DD= DE= DF= DG=	EА= EВ= EС= ED= EE= EF= EG=	FА= FВ= FС= FD= FE= FF= FG=	GА= GВ= GС= GD= GE= GF= GG=

Операция умножения выполняется только для матриц, у которых число столбцов первой матрицы равно числу строк второй.

Умножение матриц: Произведением матриц А_тk·В_kп называется такая матрица С_тn, каждый элемент которой с_ij, равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В.