Последовательность определения Pур в механизме по теореме Жуковского:

1. Построить повёрнутый на 90⁰ (в любую сторону) план скоростей механизма.

2. В соответствующие точки плана скоростей нанести все ранее определённые внешние силы (включая силы инерции и силы веса), действующие на механизм, в том числе и уравновешивающую силу P_ур.

3. Составить уравнение вида (3.9). Плечи моментов сил брать из повёрнутого плана скоростей.

4. Из составленного уравнения определить P_ур.

Пример 2. Заданы внешние силы, действующие на звенья механизма Р₂ и Р₃. Найдём уравновешивающую силу Р_ур, для чего построим план механизма в масштабе длин (рис. 3.14) и повёрнутый на 90⁰ план скоростей (рис. 3.15).

Приложим силы в соответствующие точки k и b₃ повёрнутого плана скоростей, обозначаем плечи сил. Составляем уравнение моментов сил относительно полюса плана скоростей:

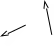
Рис. 3.14. План механизма Рис. 3.15. Повёрнутый на 90⁰

план скоростей

. Отсюда .

Если сила P_ур получается с отрицательным знаком, то её предварительно выбранное направление следует поменять на противоположное.

8. Силовой анализ рычажных механизмов с учетом сил трения

Трение в поступательной кинематической паре

При перемещении одного тела (звена механизма) относительно находящегося с ним в контакте другого тела (звена) в месте их контакта возникает сила, сопротивляющаяся перемещению, – сила трения F (рис. 3.16).

Величину коэффициента трения в поступательной кинематической паре можно определить с помощью так называемого закона Кулона, в соответствии с которым величина силы трения F прямо пропорциональна нормальной силе N между соприкасающимися звеньями. Векторная сумма сил и равна полной силе реакций в кинематической паре: (рис. 3.16).

Отношение называют коэффициентом трения скольжения в поступательной кинематической паре, а угол – углом трения скольжения.

Полная реакция отклоняется на угол трения в сторону, противоположную скорости (см. рис. 3.16).

Величину коэффициента трения скольжения f можно определить экспериментально или по справочникам (величина f зависит от шероховатости, материалов, трущихся поверхностей, наличия смазки, ее качества, температуры и т.д.).

Рис. 3.16. Схема сил в поступательной кинематической паре	Рис. 3.17. Схема сил во вращательной кинематической паре

Трение во вращательной кинематической паре

Внешние нагрузки, действующие на вал при его вращении, показаны на схеме рис. 3.17. Здесь А – точка приложения нормальной реакции , причем – равно-действующая всех нор-мальных сил (эпюра этих сил может иметь различный вид), (рис. 3.18); – сила трения (равно-действующая всех сил трения, распределенных по поверхности контакта); – сила давления цапфы вала на опору (корпус подшипника); – сила реакции во вращательной кинематической паре, ; ; – угол трения; r – радиус цапфы (опорной части) вала; – радиус круга трения; – приведенный коэффициент трения.

Во вращательной кинематической паре (см. рис. 3.15) реакция отстоит от оси вращения на величину радиуса круга трения , причем всегда касательна к кругу трения.

Момент трения .

Величину можно определить экспериментально или по эмпирическим формулам с учетом износа подшипника и соответствующего изменения эпюр давления (рис. 3.18): для нового подшипника , для изношенного – , где f – коэффициент трения скольжения в поступательной кинематической паре (берется из справочников).

Рис. 3.18. Примерные схемы эпюр давления в новом и изношенном подшипниках скольжения

Трение качения в высшей кинематической паре

Картину внешних сил и эпюр распределения давлений в месте контакта тел качения можно условно отобразить на нижеприведенных схемах (рис. 3.19). В состоянии покоя эпюра напряжений в зоне контакта симметрична относительно общей нормали, проведенной через условную точку касания, а равнодействующая сила N совпадает с нормалью. При качении симметрия эпюры нарушается, а сила N смещается в направлении качения на расстояние k.

а б

Рис. 3.19. Примерные схемы сил и эпюр давления

в зоне контакта цилиндра с плоскостью: а – состояние покоя;

б – состояние перекатывания

Здесь – равнодействующая сила давлений в месте смятия соприкасающихся звеньев (тел качения); – нагружающая сила, ; – момент трения качения; – плечо силы трения качения или коэффициент трения качения (имеет размерность длины); – сила перекатывания.

Условие равновесия перекатывающегося тела в форме моментов можно записать как , откуда .

Пример. 3.

Пусть задан кривошипно-ползунный механизм с известными внешними силами (рис. 3.20). Необходимо провести силовой анализ механизма, учитывая силы трения в кинематических парах.

А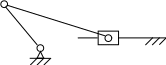

В_вр., В_пост.

0

Рис. 3.20. Кинематическая схема кривошипно-ползунного механизма

Сначала проводим силовой анализ механизма без учета сил трения (см. пример 1). При этом определяем силы реакций в кинематических парах. Затем обозначаем силы реакций в кинематических парах, радиусы цапф валов и коэффициенты трения и заносим их в таблицу.

Кинематические пары Параметры	О	А	Ввр	Впост
Силы реакций	R0	RA	RBвp	RBпост
Радиусы цапф	r0	rA	rB	-
Коэффициенты трения	f0	fA	fBвр	fBпост

Отразим трение в потерях мгновенных мощностей на трение в кинематических парах: вращательной – N = М_т  ω; поступательной – , где М_тр = Rρ = Rrf – момент трения во вращательной кинематической паре; – сила трения в поступательной кинематической паре.

Применительно к кривошипно-ползунному механизму (см. рис. 3.20) выразим потери мощностей на трение уравнением

N₀ + N_A + N_В^вр + N_B^пост = М_тр  ω₁,

где N₀, N_A, N_В^вр, N_B^пост – соответственно потери мощности на трение в кинематических парах О, А, В^вр, В^пост; ω₁ – угловая скорость кривошипа; М_тр – приведенный к кривошипу момент от всех сил трения в кинематических парах.

Тогда уравнение мощностей запишем в виде

R₀  r₀  f₀  ω₁ + R_A  r_A  f_A  (ω₁ – ω₂) + R_B^вр  r_B^вр  f_B^вр  ω₂ +

+R_B^пост  f_B^пост  V_B = M_тр  ω₁.

Из этого уравнения определяем момент трения М_тр на ведущем звене, который затем учитывается при расчете уравновешивающего момента М_ур или уравновешивающей силы Р_ур на ведущем звене механизма.