Этап №5. Формируются структурные критерии s и l, отображаемые соответствующими диагональными матрицами [s] и [l]

Рассмотрим состав упомянутых матриц.

Матрица [S] имеет следующий вид:

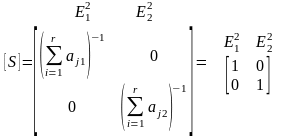
где aij — значения векторов приоритетов из матрицы [А].

С помощью матрицы [S] обеспечивается нормирование векторов приоритетов альтернатив, образующих матрицу [А], если последняя заполнена методом сравнения относительно стандартов или копирования без предварительного нормирования. Но т.к. вектора уже были нормированы на 4 этапе нормированы, то [S]- единичная.

Матрица [L] имеет следующий вид:

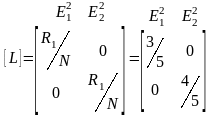
где Rj — число альтернатив Аi, находящихся под критерием Еj,

N — суммарное число альтернатив, находящихся под всеми критериями.

Здесь следует отметить, что число N в матрице [L] может приниматься равным числу рассматриваемых альтернатив r, т.е. N= r. При этом на конечный результат способ определения N не оказывает влияния.

Использование структурного критерия L позволяет эксперту или ЛПР изменять при необходимости вес альтернатив, связанных с соответствующими критериями пропорционально отношению Rj / N. Этим обеспечивается повышение приоритета альтернатив, образующих большие группы, и снижение приоритета альтернатив в группах с их относительно небольшим числом. Здесь имеется в виду, что группу определяют альтернативы, являющиеся "потомками" по отношению к критерию Ej. Необходимость в приведенной вычислительной процедуре обусловлена тем, что у критериев-"родителей" с высоким приоритетом в иерархии может находиться большое число альтернатив-"потомков", а у критериев-родителей" с низким приоритетом — значительно меньшее число альтернатив-"потомков", чем в первом случае. Поэтому в этой ситуации желательно повышение приоритетов альтернатив в большой группе, поскольку, если альтернатив много, каждая из них получит меньший составной приоритет, чем каждая альтернатива, входящая в меньшую группу с низким приоритетом критерия.

Этап №6. Вектор приоритетов альтернатив

Определяется вектор приоритетов альтернатив W относительно критериев. Данная процедура реализуется последовательным перемножением слева направо следующих матриц и векторов:

а) для случая, когда экспертные оценки в матрице [А] ненормированы:

;

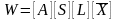б) для случая, когда экспертные оценки в матрице [А] нормированы:

Т.к. у нас матрица [А] нормирована воспользуемся второй формулой.

Для окончательного нормирования используется диагональная матрица [В]. Эта матрица имеет следующий вид:

где хi — значение ненормированного вектора приоритетов альтернатив, полученное после последовательного перемножения слева направо матриц ;

В итоге получаем, следующий нормированный вектор приоритетов альтернатив W.

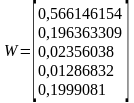
Согласно полученному результату для наилучшего удовлетворения основного критерия необходимо выбрать альтернативу А1 («Инвестирование в автомобильный завод»), т.к. она имеет наивысший рейтинг 0,566146145.

Этап №7. Оценка согласованности

Весьма полезным побочным продуктом теории является так называемый индекс согласованности (ИС), который дает информацию о степени нарушения численной и транзитивной (порядковой) согласованности. Для улучшения согласованности можно рекомендовать поиск дополнительной информации и пересмотр данных, использованных при построении шкалы. В других процедурах построения шкал отношения нет структурно порожденного индекса. Для выполнения условий согласованности в матрицах попарных сравнений используются обратные величины aji=1/aij вместо традиционно используемых при построении интервальных шкал величин aji= —aij.

Все измерения, включая те, в которых используются приборы, подвержены погрешностям измерений, а также погрешностям из—за неточностей в самом измерительном приборе. Эти погрешности могут привести к несогласованным выводам.

Вместе с матрицей парных сравнений мы имеем меру оценки степени отклонения от согласованности. Когда такие отклонения превышают установленные пределы, тому, кто проводит суждения, следует перепроверить их в матрице.

Индекс согласованности в каждой матрице и для всей иерархии может быть приближенно получен вычислениями вручную по следующему алгоритму.