Дискретизация непрерывных процессов

При замене непрерывного процесса цифровым возникают ошибки из-за квантования по уровню (шумы квантования) и дискретизации по времени (ошибки восстановления непрерывного процесса по его дискретным отсчетам). Шум квантования считается равномерно распределенным случайным процессом с дисперсией h²/12, где h – величина шага квантования. При 16-разрядном двоичном представлении числа шаг квантования равен примерно одной 65-тысячной этого числа. Поэтому шумами квантования можно пренебречь. Дискретизация заключается в замене непрерывного процесса его отсчетами, взятыми через некоторые интервалы времени Δt, не обязательно одинаковые. Далее будем рассматривать только эквидистантную дискретизацию, когда интервал дискретизации Δt постоянен.

Восстановить непрерывный процесс по его дискретным отсчетам можно без ошибки, согласно теореме Котельникова, если спектр этого процесса S(f) ограничен частотой f_гр (S(f) = 0 при f > f_гр) и частота дискретизации, f_д = =1/Δt, больше удвоенной граничной частоты (f_д ³ 2f_гр). При этом восстанавливающий фильтр должен иметь прямоугольную АЧХ и ФЧХ, равную нулю. Импульсная характеристика такого фильтра g(t) = Sin(πf_дt)/(πf_дt). Так как импульсная характеристика начинается при t = - ∞, то такой фильтр физически нереализуем. Можно использовать фильтры высокого порядка (например, Баттерворта, Чебышева и др.), АЧХ которых приближается к прямоугольной. Но повышение порядка фильтра приводит к увеличению крутизны ФЧХ, и следовательно, увеличению задержки выходного сигнала фильтра относительно входного. Таким образом, чем ближе будет форма восстановленного сигнала к исходной непрерывной, тем больше восстановленный сигнал будет задержан относительно исходного. Теоретически время задержки при идеальном восстановлении равно бесконечности.

Реально восстановление непрерывного процесса по дискретным отсчетам производится фиксацией значений процесса на интервал дискретизации с последующей фильтрацией фильтром низкой частоты.

Восстановление непрерывного процесса по дискретным отсчетам

В основе восстановления непрерывного процесса x(t) по его отсчетам x(iΔt) лежит теория аппроксимации. Аппроксимация – это замена одного математического объекта другим, в том или ином смысле близким к исходному. Для аппроксимации функций используются ряды, из которых наиболее известными являются ряд Тейлора (для экстраполяции) и ряд Лагранжа (для интерполяции).

Интерполяция – определение значений процесса внутри интервала Δt по известным значениям этого процесса на границах интервала и, возможно, в некоторых точках внутри интервала.

Экстраполяция - определение значений процесса за пределами интервала ΔT по известным значениям этого процесса, а также его производных, на границах интервала ΔT.

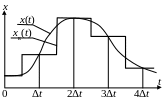
Замена непрерывного процесса ступенчатым Простейшей аппроксимацией является ступенчатая. При ступенчатой интерполяции восстановленный процесс x_в(t) на интервале iΔt – Δt/2 < t < iΔt + Δt/2 считается равным значению отсчета процесса в момент времени t = iΔt (рис. 4.1 а). Таким образом, в интервале между соседними отсчетами процесс изменяется скачком в середине интервала.

а)	б)
Рис. 4.1

При ступенчатой экстраполяции (рис. 4.1 б) восстановленный процесс принимает значение отсчета в момент времени t = iΔt на всю длину последующего интервала.

С тупенчатая интерполяция физически не реализуема, так как в середине интервала процесс должен принять значение, которое в этот момент еще не известно, а будет известно позже, в следующий момент дискретизации. Ступенчатая экстраполяция физически реализуема, так как для восстановления процесса требуется знание только предыдущего отсчета. Схему, осуществляющую ступенчатую экстраполяцию называют фиксатором нулевого порядка. Такое преобразование производит ЦАП. Импульсная характеристика фиксатора нулевого порядка показана на рис 4.2. Формирование ступенчатого процесса можно представить как реакцию фильтра с такой импульсной характеристикой на последовательность δ-импульсов, площадь которых равна x(iΔt).

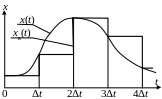
Замена непрерывного процесса кусочно-линейным Замена непрерывного процесса кусочно-линейным осуществляется в результате линейной интерполяции или экстраполяции. При линейной интерполяции (рис. 4.3 а) восстановленный процесс изменяется внутри интервала дискретизации линейно, принимая на границах этого интервала значения отсчетов исходного процесса. При линейной экстраполяции (рис. 4.3 б) восстановленный процесс тоже изменяется линейно внутри интервала дискретизации, но эта линия строится как продолжение линии, построенной по отсчетам процесса на границах предыдущего интервала дискретизации.

x x(t) xв(t) t 0 Δt 2Δt 3Δt 4Δt	t x x(t) xв(t) 0 Δt 2Δt 3Δt 4Δt
а)	б)
Рис. 4.3.

Линейная интерполяция, так же, как и ступенчатая, физически не реализуема, так как нельзя провести прямую линию из точки, соответствующей началу интервала, в точку, координаты которой еще не известны. Линейная экстраполяция физически реализуема, но восстановленный процесс может значительно отличаться от исходного непрерывного, особенно на участках, где производная меняет знак, и использование линейной экстраполяции нецелесообразно.

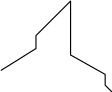
Линейную интерполяцию можно реализовать, если допустить задержку результата интерполяции на один интервал дискретизации (рис. 4.4). Тогда становятся известными координаты конца отрезка прямой, и с этого момента можно строить интерполирующую прямую.

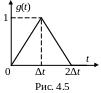
Устройство, реализующее такую интерполяцию, называется фиксатором первого порядка. Его импульсная характеристика показана на рис 4.5.

Ошибки дискретизации

Как видно из приведенных выше рисунков (рис. 4.1 б и рис. 4.4), исходный x(t) и восстановленный x_в(t) процессы отличаются друг от друга. Различие между ними называется ошибкой дискретизации. Эту ошибку можно определить по-разному. На рис.4.6 показаны два подхода к определению ошибки.

В системах передачи информации, где несущественна задержка, вносимая устройством восстановления сигнала, пользуются ошибкой без учета задержки. Она равна разности исходного задержанного процесса и восстановленного процесса, причем задержка выбирается такой (t_опт), чтобы ошибка была минимальной. Эта ошибка является ошибкой интерполяции:

δ_инт(t) = x(t – t_опт) – x_в(t).

В системах с обратной связью задержка восстановленного сигнала нежелательна. Она может привести не только к увеличению ошибок моделирования, но и к потере устойчивости модели. В этом случае ошибка определяется как:

δ_полн(t) = x(t) – x_в(t)

и называется полной ошибкой. На рис. 4.7 приведены осциллограммы полной ошибки и ошибки интерполяции при восстановлении процесса фиксаторами нулевого и первого порядков, когда исходный процесс представляет собой отрезок синусоиды длительностью в один период, а отношение периода синусоиды к интервалу дискретизации равно 10.

а) Полная ошибка для фиксатора нулевого порядка	б) Ошибка интерполяции для фиксатора нулевого порядка
в) Полная ошибка для фиксатора первого порядка	б) Ошибка интерполяции для фиксатора первого порядка
Рис 4.7

Так как ошибки зависят от времени, то для их числовой оценки используется среднеквадратическая ошибка, усредненная за время Т, в течение которого измеряется ошибка:

t₀+T

С

t₀

КО = (1/Т)∫δ²(t)dt. (4.1)

Сравнивая графики, приведенные на рис. 4.7, видим, что полная ошибка для фиксатора нулевого порядка меньше, чем для фиксатора первого порядка. Это связано с тем, что для фиксатора нулевого порядка восстановленный процесс задержан относительно исходного на половину интервала дискретизации, а для фиксатора первого порядка – на интервал дискретизации. Ошибка интерполяции, наоборот, меньше для фиксатора первого порядка.