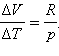6) Физический смысл и свойства энтальпии идеального газа.
|
Рассмотрим полную энергию газа, находящегося под давлением Р, создаваемым грузом G (рисунок 1.3.1), расположенном на поршне (дробь). Площадь поперечного сечения F в условиях равновесия давления газа Р и груза G будет G = Р∙F. В этом случае полная энергия Е будет состоять из внутренней энергии газа U и потенциальной энергии груза, равной G∙h = Р∙F∙h = Р∙V, то есть Е = U + Р∙V, (1.3.9) где V – объем занимаемый газом, V = F∙h. Величина Р∙V, зависящая от сил, действующих на поршень, получила название потенциальной энергии давления. Таким образом, если газ находится под давлением Р, то с любым его состоянием связана некоторая энергия U + Р∙V = I, получившая на звание энтальпии газа в данном состоянии. Выражение для удельной энтальпии имеет вид: i = u + P ∙v. (1.3.10) Следовательно, энтальпия, будучи образованной из параметров состояния U, Р, V является однозначной функцией состояния, то есть параметром состояния. Поэтому изменение Δi, как и изменение Δu, не зависит от характера процесса, а зависит только от начального и конечного состояния Δi = i2 – i1 = (u2 + Р2∙V2) – (u1 + Р1V1). (1.3.11)
|
Энтальпия идеального газа, как и внутренняя энергия, является функцией только температуры, ибо
Δi = (u2 + R∙T2) – (u1 + R∙T1), (1.3.12)
но так как доказано, что внутренняя энергия U зависит только от температуры, то из этого выражения видно, что и энтальпия зависит толь ко от температуры.
Понятие энтальпии широко применяется в расчетах тепловых процессов, особенно графическими методами. Особое значение энтальпия приобретает при рассмотрении термодинамики потока газа или пара, где она приобретает смысл так называемой внутренней потенциальной энергии потока.
Так как в технической термодинамике не требуется знания абсолютного значения энтальпии, то она обычно отсчитывается от некоторого условного нуля (для газов iо = 0 при t = 0 °С ). Единицей измерения удельной энтальпии i служит Дж/кг или кДж/кг.
Ее физический смысл в том, что при постоянном давлении изменение энтальпии (теплосодержания) равно количеству тепла, получаемому телом: d(Q)=d(H) и которое идет на :
на изменение внутренней энергии dU (через изменение температуры тела);
на совершение работы над внешней средой PdV (через изменение объема).
Очевидно, что если тело теплоизолировано (не получает тепла), то Н = const, и dH = 0.
7) Теплоемкость идеального газа. Зависимость теплоемкости от термических параметров состояния.
Теплоемкость весьма важная физическая величина, зная ее, можно определить количество теплоты, подведенное (отведенное) к рабочему телу, изменение его внутренней энергии, энтальпии и т.п.
Под теплоемкостью газа понимают количество теплоты, которое необходимо сообщить ему для повышения температуры на один градус.
Теплоемкость
относится к категории экстенсивных
величин и может быть преобразована в
интенсивную величину путем деления ее
на массу, объем или количество вещества.
Применительно к газам различают удельную
массовую теплоемкость C,
Дж/кг*К; объемную
,
Дж/м3*К;
и молярную
,
Дж/моль*К теплоемкости.
Экспериментальные, а также теоретические исследования показывают, что теплоемкость газов есть величина переменная, зависящая от температуры и давления, однако теплоемкости идеальных газов от давления не зависят, так как являются функциями только одной температуры.
Одновременно теплоемкости как идеальных, так и реальных га- зов зависят от природных свойств газа и условий протекания термодинамического процесса.
Если бы теплоемкость не зависела от температуры, то она была бы величиной постоянной для данного газа и изображалась бы в координатах с-t (рисунок 1.5.1) прямой линией 1, параллельной оси абсцисс.
Переменная теплоемкость, зависящая от температуры тела, изображается в этой же системе координат линией 2 при прямолинейной зависимости теплоемкости от температуры и линии 3 при криволинейной зависимости.
В теплотехнических расчетах часто зависимость теплоемкости от давления или объема не учитывают и пользуются значениями теплоемкости реальных газов как функции только температуры. Эти значения обычно приводятся в таблицах.
|
В тепловых же расчетах паровых и водогрейных котлов, термических печей, двигателей внутреннего сгорания и т.п. приходится считаться с зависимостью теплоемкости от температуры, и поэтому используются переменные теплоемкости (рисунок 1.5.1). Табличные данные часто сводят в формулы типа сх=ах+в·t – линейная зависимость, (1.5.1) сх=ах+ в·t+ d·t2 + ... – криволинейная зависимость, где ах, в, d ... – постоянные коэффициенты для данного газа. При t=0 °С получим ах = сх, то есть коэффициент ах представляет теплоемкость тела при температуре 0 °С. |
Под средней теплоемкостью понимают такую теплоемкость в за- данном интервале температур, при использовании которой в расчетах получается количество теплоты, участвующее в действительном термодинамическом процессе. При этом процесс с переменной теплоемкостью заменяется фиктивным процессом с постоянной теплоемкостью при условии получения такого же количества теплоты, как и в действительно протекающем процессе.
Чем меньше разность температур, тем больше приближается средняя теплоемкость к значению действительной или так называемой истинной теплоемкости. Следовательно, истинной теплоемкостью называется средняя теплоемкость для бесконечно малого температурного интервала.
В процессе при постоянном объеме газ работы не совершает: A = 0. Из первого закона термодинамики для 1 моля газа следует
|
Изменение ΔU внутренней энергии газа прямо пропорционально изменению ΔT его температуры.
Для процесса при постоянном давлении первый закон термодинамики дает:
|
где ΔV – изменение объема 1 моля идеального газа при изменении его температуры на ΔT. Отсюда следует:
|
Отношение ΔV / ΔT может быть найдено из уравнения состояния идеального газа, записанного для 1 моля:
pV = RT, |
где R – универсальная газовая постоянная. При p = const
|
или
Таким образом, соотношение, выражающее связь между молярными теплоемкостями Cp и CV, имеет вид (формула Майера):
Cp = CV + R. |