32. Закон Фурье.

Согласно закону теплопроводности Фурье, количество теплоты δQ,

проходящее через элементарную площадку пропорционально площади этой

площадки dF , расположенной на изотермической поверхности, промежутку времени dτ и температурному градиенту grad t.

Градиентом температуры grad t называется предел отношения изменения

температуры Δt к расстоянию между изотермами Δn, когда Δn стремится к нулю:

Температурный градиент есть вектор, направленный по нормали к изотермической поверхности в сторону возрастания температуры.

33. Коэффициент теплопроводности. Физический смысл. Свойства.

Коэффициент теплопроводности λ характеризует способность данного вещества проводить тепло и зависит, главным образом, от строения, плотности веществ и их параметров. Для диэлектриков, к которым относится испытуемый материал, коэффициент λ зависит от влажности, пористости. В теории теплопроводности существует аналитическое описание стационарного температурного поля для тел правильной геометрической формы (пластины, цилиндры, шары). Тела этих форм и выбирают за экспериментальные образцы.

Физический смысл λ: численно равен количеству тепла, проходящему в единицу времени (1 с) через стенку толщиной 1 м, ограниченную изотермическими поверхностями площадью 1м^2 при разности температур

между ними 1 К.

34. Дифференциальное уравнение теплопроводности.

Уравнение теплопроводности — важное уравнение в частных производных, которое описывает распространение тепла в заданной области пространства во времени.

Для функции u(x,y,z,t) трёх пространственных переменных (x,y,z) и времени t, уравнение теплопроводности имеет вид:

Уравнение называется дифференциальным уравнением теплопроводности, или уравнением Фурье, для трехмерного нестационарного температурного поля при отсутствии внутренних источников тепла. Оно является основным уравнением при изучении вопросов нагревания и охлаждения тел в процессе передачи теплоты тепло­проводностью и устанавливает связь между временным и пространст­венным изменениями температуры в любой точке поля.

35. Граничные условия 1-го и второго рода.

Дифференциальное уравнение теплопроводности является математической моделью целого класса явлений теплопроводности и само по себе ничего не говорит о развитии процесса теплопереноса в рассматриваемом теле. При интегрировании дифференциального уравнения в частных производных получаем бесчисленное множество различных решений.Чтобы получить из этого множества одно частное решение, соответствующее определенной конкретной задаче, необходимо иметь дополнительные данные, не содержащиеся в исходном дифференциальном уравнении теплопроводности. Этими дополнительными условиями, которые в совокупности с дифференциальным уравнением (или его решением) однозначно определяют конкретную задачу теплопроводности, являются распределение температуры внутри тела (начальные или временные условия), геометрическая форма тела и закон взаимодействия между окружающей средой и поверхностью тела (граничные условия).

Для тела определенной геометрической формы с определенными (известными) физическими свойствами совокупность граничных и начальных условий называется краевыми условиями. Итак, начальное условие является временным краевым условием, а граничные условия – пространственным краевым условием. Дифференциальное уравнение теплопроводности вместе с краевыми условиями составляет краевую задачу уравнения теплопроводности (или короче – тепловую задачу).

Начальное условие определяется заданием закона распределения температуры внутри тела в начальный момент времени, т. е.

Т (х, у, z, 0) = f (х, у, z), (3.1)

где f (х, у, z) — известная функция.

Во многих задачах принимают равномерное распределение температуры в начальный момент времени; тогда

Т (х, у, z, 0) = То = const. (3.2)

Граничное условие может быть задано различными способами.

1. Граничное условие первого рода состоит в задании распределения температуры по поверхности тела в любой момент времени,

Тs (τ) = f(τ) (3.3)

где Тs (τ) – температура на поверхности тела.

Изотермическое граничное условие представляет частный случай условия 1-го рода. При изотермической границе температуру поверхности тела принимают постоянной Ts= const, как, например, при интенсивном омывании поверхности жидкостью с определенной температурой.

2. Граничное условие второго рода состоит в задании плотности теплового потока для каждой точки поверхности тела как функции времени, т. е.

qs (τ) = f(τ). (3.4)

Условие 2-го рода задает величину теплового потока на границе, т.е. кривая температуры может иметь любую ординату, но обязательно заданный градиент. Простейший случай граничного условия второго рода состоит в постоянстве плотности теплового потока:

qs (τ) = qc = const.

Адиабатическая граница представляет частный случай условия 2-го рода. При адиабатическом условии тепловой поток через границы равен нулю. Если теплообмен тела с окружающей средой незначителен в сравнении с тепловыми потоками внутри тела, поверхность тела можно считать практически не пропускающей тепло. Очевидно, что в любой точке адиабатической границы s удельный тепловой поток и пропорциональный ему градиент по нормали к поверхности равны нулю.

35. Граничные условия 1-го и второго рода.

36. Граничные условия 3-го рода.

1. Граничные условия первого рода, когда на поверхности, ограничивающей исследуемую область, задано распределение температур как функция координат и времени:

T_пов = (x, y, z, ).                   (3.15)

В горно-теплофизических расчетах граничные условия первого рода могут быть использованы при постановке задач, описывающих температурные поля в породах, окружающих горные выработки, при интенсивном испарении влаги с поверхности пород при движении теплоносителя по скважинам или геотермальному коллектору в системах извлечения геотермальной энергии и т.п.

2. Граничные условия второго рода, когда на поверхности в функции координат и времени задана плотность теплового потока, т.е. производная от температуры по нормали к поверхности:

          (3.16)

Возможен случай задания однородного граничного условия второго рода

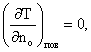                                        (3.17)

т.е. условия отсутствия потока теплоты на поверхности тела, так называемая тепловая изоляция. Такое условие часто задается при равномерном обогреве поверхности тела, имеющего геометрическую симметрию. Например, задача симметричного прогрева пластины толщиной 2R(х < R), являющаяся, например, физической моделью для исследования формирования температурных полей в ленточном целике, когда на ограничивающих поверхностях х = R с помощью инфракрасных излучателей задана плотность тепловых потоков q₁ = q₂ = q_о) сводится к эквивалентной задаче: заданы тепловой поток q_о на поверхности х = R и условие (3.7), т.е. q = 0, в центре симметрии пластины х = 0. Другой пример задания условия второго рода относится к формированию в горном массиве заданного температурного распределения с помощью установленной в выработке холодильной машины. Плотность теплового потока при этом равна отношению тепловой мощности холодильной машины Q() к поверхности выработки F, т.е. q = Q()/F.

3. Граничные условия третьего рода, в которых тепловой поток предполагается пропорциональным разности температуры поверхности твердого тела, описываемого жидкостью Т_пов., и температуры жидкости t:

     (3.18)

Граничное условие третьего рода широко применяется в горной теплофизике для исследования температурных полей в системе горный массив - воздушная струя, а также при фильтрации газа и жидкости в пористых средах.

4. Граничные условия четвертого рода сводятся к одновременному заданию равенства температур и тепловых потоков на границе раздела , когда решается задача о теплообмене двух сред с температурами Т₁(x, y, z, ), T₂(x, y, z, ), например, твердое тело - жидкость, твердое тело - твердое тело, жидкость - жидкость), в каждой из которых перенос теплоты описывается своим уравнением энергии:

                          Т₁ = Т₂;              (3.19)

          (3.20)

Равенство (3.19) выражает условие непрерывности температурного поля, а равенство (3.20) - закон сохранения энергии на поверхности соприкосновения двух сред (или тел). Условия (3.19), (3.20) называются еще условиями идеального теплового контакта, а также неуправляемыми граничными условиями в отличие от граничных условий первого - третьего родов (управляемые граничные условия).

В задачах горной теплофизики граничные условия четвертого рода в основном используются при вычислении температурных полей в неоднородных по теплофизическим свойствам породных массивах, находящихся в контакте друг с другом, например, бетонная закладка - руда, гидравлическая закладка - уголь, бетонная крепь - горный массив.

Таким образом, при конвективном теплообмене твердого тела с жидкостью в случае стационарного температурного поля (Т/ = 0) целесообразно использовать граничные условия третьего рода - соотношение (3.18), а в случае нестационарного поля (Т/  0)          при точной формулировке задачи необходимо применять граничные условия четвертого рода (3.19), (3.20). В случае нестационарного лучистого теплообмена при большой разности температур поверхности и среды необходимо применять граничные условия второго рода (соотношение (3.16)). При малой разнице температур, когда [T_пов() - t()]  0, можно использовать закон Ньютона, т.е. граничные условия третьего рода.

37. Теплопроводность бесконечной плоской пластины в граничных условиях 1-го рода.

3. Теплопроводность в стенке (граничные условия 1-ого рода).

Теплопроводность однослойной стенки.

Рассмотрим однородную плоскую стенку толщиной . На наружных поверхностях стенки поддерживаются постоянные во времени температуры t_c1 и t_c2. Теплопроводность материала стенки постоянна и равна .

При стационарном режиме , кроме того, температура изменяется только в направлении, перпендикулярном плоскости стеки (ось 0х): . Поэтому уравнение теплопроводности имеет вид: .

Постоянные С₁ и С₂ в уравнении определим из граничных условий I рода:

при х = 0: t = t_c1 и C₂ = t_c1;

при х = : t = t_c2 и C₁ = –(t_c1 – t_c2)/ .

Следовательно:

Определим плотность теплового потока через плоскую стенку. В соответствии с законом Фурье с учетом равенства (*) можно написать: .

Следовательно (**).

Разность значений температуры в уравнении (**) называется температурным напором. Из этого уравнения видно, что плотность теплового потока q изменяется прямо пропорционально теплопроводности  и температурному напору t и обратно пропорционально толщине стенки .

Отношение называется тепловой проводимостью стенки, а обратная ему величина – термическим сопротивлением стенки.

Общее количество теплоты, которое передается через поверхность стенки площадью F за промежуток времени : .

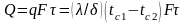Теплопроводность  следует брать при средней температуре стенки.

38. Теплопроводность многослойной плоской стенки в граничных условиях 3-го рода.

39. Теплопередача. Коэффициент теплопередачи для плоской стенки.

Теплопередача через плоскую стенку

Теплопередачей называется передача теплоты от горячего теплоносителя к холодному теплоносителю через стенку, разделяющую эти теплоносители. Примерами теплопередачи являются: передача теплоты от греющей воды нагревательных элементов (отопительных систем) к воздуху помещения; передача теплоты от дымовых газов к воде через стенки кипятильных труб в паровых котлах; передача теплоты от раскаленных газов к охлаждающей воде (жидкости) через стенку цилиндра двигателя внутреннего сгорания; передача теплоты от внутреннего воздуха помещения к наружному воздуху и т. д. При этом ограждающая стенка является проводником теплоты, через которую теплота передается теплопроводностью, а от стенки к окружающей среде конвекцией и излучением. Поэтому процесс теплопередачи является сложным процессом теплообмена. При передаче теплоты от стенки к окружающей среде в основном преобладает конвективный теплообмен, поэтому будут рассматриваться такие задачи. 1). Теплопередача через плоскую стенку. Рассмотрим однослойную плоскую стенку толщиной  и теплопроводностью  (рис12.1).

 Температура горячей жидкости (среды) t^'_ж, холодной жидкости (среды) t^''_ж. Количество теплоты, переданной от горячей жидкости (среды) к стенке по закону Ньютона-Рихмана имеет вид:

 

Q = ₁ · (t^'_ж – t₁) · F, (12.1)

где ₁ – коэффициент теплоотдачи от горячей среды с температурой t^'_ж к поверхности стенки• с температурой t₁; F – расчетная поверхность плоской стенки. Тепловой поток, переданный через стенку определяется по уравнению:

Q = / · (t₁ – t₂) · F. (12.2)

Тепловой поток от второй поверхности стенки к холодной среде определяется по формуле:

Q = б₂ · (t₂ - t^''_ж) · F, (12.3)

где ₂ – коэффициент теплоотдачи от второй поверхности стенки к холодной среде с температурой t^''_ж. Решая эти три уравнения получаем:

Q = (t^'_ж – t^''_ж) • F • К, (12.4)

где К = 1 / (1/₁ + /  + 1/₂) – коэффициент теплопередачи, (12.5) или

R₀ = 1/К = (1/₁ + / + 1/₂) – полное термическое сопротивление теплопередачи через однослойную плоскую стенку. (12.6)

1/₁, 1/₂ – термические сопротивления теплоотдачи поверхностей стенки; / - термическое сопротивление стенки.

Теплопередача

        Теплообмен между двумя теплоносителями через разделяющую их твёрдую стенку или черезповерхность раздела между ними. Т. включает в себя теплоотдачу (См. Теплоотдача) от более горячейжидкости к стенке, Теплопроводность в стенке, теплоотдачу от стенки к более холодной подвижной среде.Интенсивность передачи теплоты при Т. характеризуется коэффициентом Т. k, численно равным количествутеплоты, которое передаётся через единицу поверхности стенки в единицу времени при разноститемператур между жидкостями в 1 К; размерность k — вт/(м²․К) [ккал/м²․°С)]. Величина R, обратнаякоэффициенту Т., называется полным термическим сопротивлением Т. Например, R однослойной стенки

        

        ,

        где α₁ и α₂ — коэффициенты теплоотдачи от горячей жидкости к поверхности стенки и от поверхностистенки к холодной жидкости; δ — толщина стенки; λ— коэффициент теплопроводности. В большинствевстречающихся на практике случаев коэффициент Т. определяется опытным путём. При этом полученныерезультаты обрабатываются методами подобия теории (См. Подобия теория). См. также Конвективныйтеплообмен.

40. Теплоотдача. Физический смысл коэффициента теплоотдачи.

ТЕПЛООТДАЧА - теплообмен (конвективный или лучистый) между поверхностью тела и окружающей средой. Интенсивность теплоотдачи характеризуется коэффициентом теплоотдачи, равным плотности теплового потока на поверхности раздела, отнесенной к температурному напору между средой и поверхностью.

Теплоотдача — это процесс теплообмена между теплоносителем и твёрдым телом.

Физический смысл коэффициента теплоотдачи представляет собой следующее: это – количество теплоты, теряемое (или воспринимаемое) в единицу времени единицей поверхности тела, когда разность температур между поверхностью тела и средою составляет один Кельвин.

Следовательно, теплоотдача тела в первую очередь определяется разностью

температур тела и окружающей среды (температурным напором). Кроме того, интенсивность теплоотдачи зависит также от физических свойств среды, от формы и положения тела и ряда других факторов. Коэффициент теплоотдачи определяется из известного соотношения:

где Qк – количество тепла, переданное нагретым телом в единицу времени

путем конвекции в ваттах;

F – поверхность тела, в м2 ;

tс – температура поверхности тела в град;

tж – температура жидкости (газа), в град.

Теплоотдача

I Теплоотда́ча

        в технике, Теплообмен между поверхностью твёрдого тела и соприкасающейся с ней средой —теплоносителем (См. Теплоноситель) (жидкостью, газом и т. д.). Т. происходит конвекцией (См. Конвекция),Теплопроводностью, лучистым теплообменом (См. Лучистый теплообмен). Различают Т. при свободном ивынужденном движении теплоносителя, а также при изменении его агрегатного состояния. ИнтенсивностьТ. характеризуется коэффициентом Т. — количеством теплоты, переданным в единицу времени черезединицу поверхности при разности температур между поверхностью и средой — теплоносителем в 1 К. Т.можно рассматривать как часть более общего процесса теплопередачи (См. Теплопередача). См. также