23. Энтропия изолированной системы. Физический смысл энтропии.

Поскольку для изолированной (адиабатной) системы с обратимыми процессами dq = 0, то) можно записать:

dS = 0 .

Отсюда следует, что энтропия изолированной системы, в которой протекают только обратимые процессы, остается постоянной (S2 = S1 = const).

Энтропия изолированной системы будет возрастать, если в ней имеют место необратимые процессы:

dS > 0; S2 > S1.

Как известно, все самопроизвольные процессы являются необратимыми. Если изолированная термодинамическая система находится в начальном неравновесном состоянии, то внутри нее будут протекать самопроизвольные процессы обмена энергией между отдельными телами до тех пор, пока система в целом не придет в равновесное состояние. При этом энтропия отдельных тел, входящих в систему, может увеличиваться или уменьшаться, в зависимости от того, подводится к ним теплота или отводится. Но энтропия изолированной системы при этом будет только возрастать.

Сказанное позволяет рассматривать энтропию как величину, характеризующую меру необратимости процессов, протекающих в изолированной системе.

.При выполнении обратимых процессов в адиабатной системе (как было показано ранее) ее энтропия остается постоянной, но энтро­пия отдельных частей системы может претерпевать изменения. При наличии внутри системы теплообмена между различными телами, эн­тропия тел, отдающих теплоту, уменьшается настолько, насколько увеличивается энтропия тел, воспринимающих теплоту. Поэтому, даже если предположить, что преобразование теплоты в работу, которое имеет место в тепловых двигателях, не сопровождается потерями энергии, то все равно часть теплоты, попадая в окружающую среду, обесценивается, а энтропия приемника обесцененной теплоты окру­жающей среды - растет. В связи с вышеизложенным, можно опреде­лить физический смысл энтропии, который будет состоять в том, что эта функция состояния (энтропия), рассматриваемая приме­нительно к окружающей среде (воздуху, земле, воде), является ме­рой энергии, потерявшей цену для дальнейшего выполнения рабо­ты.

24. Второй закон термодинамики для обратимых и необратимых процессов.

η_tk.o=1- → →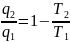

Так как q2 это отводимое количество теплоты и, следовательно,

его алгебраическое значение по смыслу отрицательно, то вместо q₂/T₂ запишем -q₂/T₂

т. е. для обратимого цикла Карно алгебраическая сумма частных, полученных от деления количества теплоты на абсолютную температуру, при которой эта теплота подводится или отводится, равна нулю. Покажем, что это утверждение справедливо для любого обратимого кругового процесса. Как было показано выше, любой произвольно взятый цикл можно представить как сумму бесконечно большого числа элементарных циклов Карно.

Для каждого такого цикла и, следовательно, для всего цикла АВСДА где - интеграл, взятый по замкнутому контуру АВСD. Это уравнение называется интегралом Клаузиуса. Следовательно, для любого обратимого цикла интеграл Клаузиуса равен нулю. Введем для подынтегральной функции интеграла Клаузиуса следующее обозначение

Тогда уравнение, приведенное выше можно записать так

Из математики известно, что если криволинейный интеграл равен нулю, то дифференциал подынтегральной функции есть полный дифференциал. Следовательно, dS есть полный интеграл некоторой функции S. С термодинамической точки зрения функция S, изменение которой не зависит от процесса, а только от начального и конечного состояний, есть параметр термодинамического состояния вещества, и, как уже было показано выше, она была названа Клаузиусом− энтропией. Таким образом, для любого обратимого цикла можно записать, что

или δq = T·dS.

Эти уравнения представляют собой аналитическое выражение второго закона термодинамики для обратимых процессов.

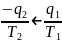Для необратимого цикла Карно η_tk.н= η_tk.o=1- откуда следует, что или или т.е.

Любой произвольно взятый необратимый процесс АВСДА можно

представить как сумму бесконечно большого числа элементарных не-

обратимых циклов Карно, для каждого из которых 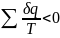и поэтому для необратимого цикла АВСДА Но для рабочего тела, совершающего цикл и, следовательно,

Отсюда можно написать, что < dS, или необратимость процесса связана с увеличением энтропии по сравнению с обратимым. Отсюда следует, что δq < Т·dS.

25. Цикл ДВС с подводом теплоты при V=const, его термический КПД

Цикл с подводом теплоты при V=const является прототипом рабочего процесса в двигателях с принудительным зажиганием (зажиганием горючей смеси происходит от электрической искры). Отличительной особенностью таких двигателей является сжатие горючей смеси (смеси паров бензина с воздухом). Этот цикл состоит из двух адиабат и двух изохор. Адиабата 1-2 отвечает сжатию горючей смеси, изохора 2-3 сгоранию смеси, изохора 2-3 сгоранию смеси (подвод теплоты q₁), вследствие чего давление повышается до p_3. После этого продукты сгорания адиабатно расширяются (процесс 3-4). В изохорном процессе 4-1 от газа отводится теплота q_2.

η_t,v=1-

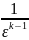
26. Цикл ДВС с подводом теплоты при (p=const) и его термодинамический КПД

Идеальный цикл ДВС с подводом теплоты при (p=const) состоит из двух адиабат, изобары и изохоры и являются образцом для двигателей тяжелого топлива, которые называются копрессорными дизелями. В этих двигателях сначала сжимается по адиабате 1-2 чистый воздух, в результате чего его температура повышается до требуемой температуры самовоспламенения топлива.

Затем в изобарном процессе 2-3 происходит впрыск и горение топлива (подвод теплоты q₁). Далее происходит адиабатное расширение 3-4 и изохорный выхлоп 4-1 (отвод теплоты q₂). η_t,p=1-