Задание №15.Планиметрия(базовый уровень)

Вариант № 53804

1. B 15 . 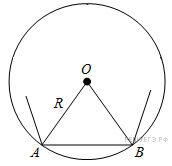Угол между сто­ро­ной пра­виль­но­го n-уголь­ни­ка, впи­сан­но­го в окруж­ность, и ра­ди­у­сом этой окруж­но­сти, про­ве­ден­ным в одну из вер­шин сто­ро­ны, равен . Най­ди­те n.

По­яс­не­ние.

Рас­смот­рим тре­уголь­ник Он рав­но­бед­рен­ный, т. к. Зна­чит, Тогда

 

Ответ: 4.

Ответ: 4

2. B 15 . 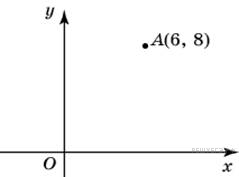Най­ди­те ор­ди­на­ту точки, сим­мет­рич­ной точке A(6; 8) от­но­си­тель­но оси Ox.

По­яс­не­ние.

Так как точка сим­мет­рич­на от­но­си­тель­но оси Ox, то абс­цис­са равна 6, а ор­ди­на­та равна −8.

 

Ответ: −8.

Ответ: -8

3. B 15 .

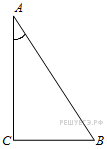В тре­уголь­ни­ке ABC угол C равен 90°, , . Най­ди­те AC.

По­яс­не­ние.

Вы­пол­ним пре­об­ра­зо­ва­ния:

.

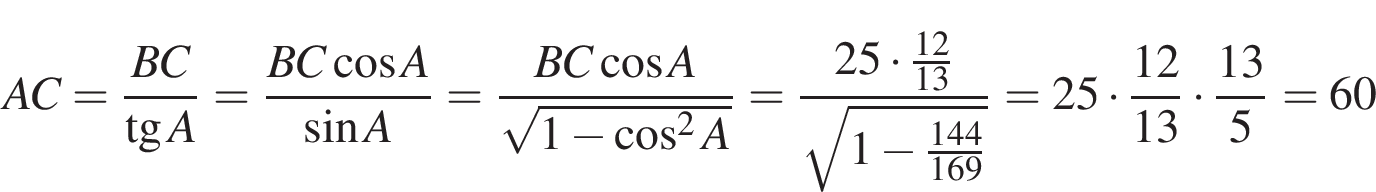Ответ: 60.

Ответ: 60

4. B 15 . Най­ди­те пло­щадь ромба, если его диа­го­на­ли равны 4 и 12.

По­яс­не­ние.

Пло­щадь ромба равна по­ло­ви­не про­из­ве­де­ния его диа­го­на­лей. По­это­му

 

.

Ответ: 24.

Ответ: 24

5. B 15 . 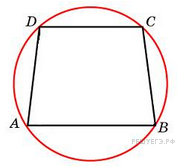Ос­но­ва­ния рав­но­бед­рен­ной тра­пе­ции равны 8 и 6. Ра­ди­ус опи­сан­ной окруж­но­сти равен 5. Най­ди­те вы­со­ту тра­пе­ции.

По­яс­не­ние.

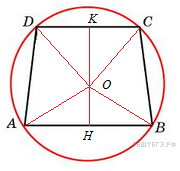вы­со­та тра­пе­ции и – вы­со­ты рав­но­бед­рен­ных тре­уголь­ни­ков и По тео­ре­ме Пи­фа­го­ра:

 

Тогда

Ответ: 7.

Ответ: 7

6. B 15 . 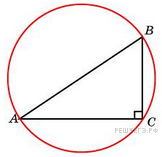В тре­уголь­ни­ке , , угол равен 90°. Най­ди­те ра­ди­ус опи­сан­ной окруж­но­сти этого тре­уголь­ни­ка.

По­яс­не­ние.

впи­сан­ный угол, опи­ра­ю­щий­ся на диа­метр окруж­но­сти, яв­ля­ет­ся пря­мым, зна­чит, – диа­метр.

 

Ответ: 2,5.

Ответ: 2,5

7. B 15 .

В тре­уголь­ни­ке ABC угол C равен 90°, , . Най­ди­те BC.

По­яс­не­ние.

Имеем:

 

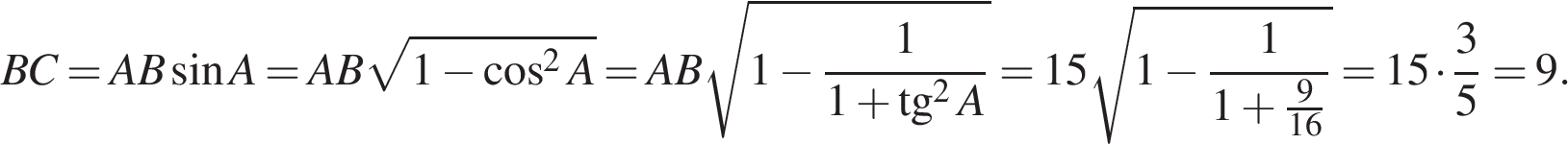
Ответ: 9.

Ответ: 9

8. B 15 . Най­ди­те уг­ло­вой ко­эф­фи­ци­ент пря­мой, про­хо­дя­щей через точки с ко­ор­ди­на­та­ми и

По­яс­не­ние.

Уго­ло­вой ко­эф­ф­ци­ент пря­мой опре­де­ля­ет­ся по фор­му­ле:

 

Ответ: −16.

Ответ: -16

9. B 15 . 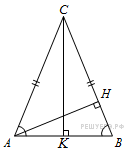В тре­уголь­ни­ке ,  — вы­со­та, . Най­ди­те .

По­яс­не­ние.

Тре­уголь­ник рав­но­бед­рен­ный, зна­чит, углы и равны как углы при его ос­но­ва­нии и вы­со­та, про­ве­ден­ная из точки делит ос­но­ва­ние по­по­лам.

 

.

Ответ: 24.

Ответ: 24

10. B 15 . 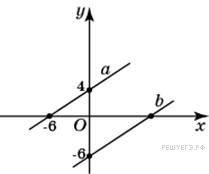Пря­мая a про­хо­дит через точки с ко­ор­ди­на­та­ми (0; 4) и (−6; 0). Пря­мая b про­хо­дит через точку с ко­ор­ди­на­та­ми (0; −6) и па­рал­лель­на пря­мой a. Най­ди­те абс­цис­су точки пе­ре­се­че­ния пря­мой b с осью Ox.

Вариант № 55801

1. B 15 .

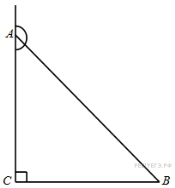
В тре­уголь­ни­ке угол равен 90°, синус внеш­не­го угла при вер­ши­не равен , . Най­ди­те .

По­яс­не­ние.

 

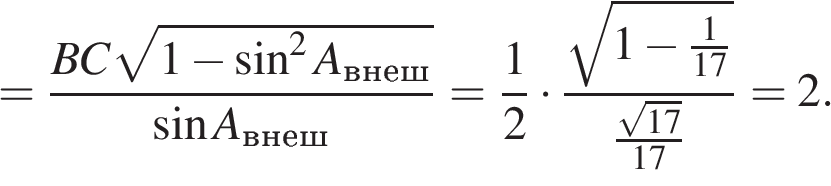
Ответ: 2.

Ответ: 2

2. B 15 . 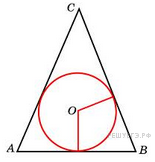Окруж­ность, впи­сан­ная в рав­но­бед­рен­ный тре­уголь­ник, делит в точке ка­са­ния одну из бо­ко­вых сто­рон на два от­рез­ка, длины ко­то­рых равны 5 и 3, счи­тая от вер­ши­ны, про­ти­во­ле­жа­щей ос­но­ва­нию. Най­ди­те пе­ри­метр тре­уголь­ни­ка.

По­яс­не­ние.

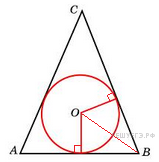Пусть точки H и K яв­ля­ют­ся точ­ка­ми ка­са­ния окруж­но­сти и сто­рон AB и СВ со­от­вет­ствен­но. Тре­уголь­ни­ки и равны, т. к. яв­ля­ют­ся пря­мо­уголь­ны­ми с общей ги­по­те­ну­зой и рав­ны­ми ка­те­та­ми, зна­чит,

 

 

Ответ: 22.

Ответ: 22

3. B 15 . 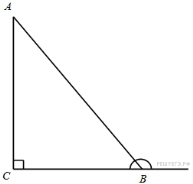В тре­уголь­ни­ке угол равен 90°, . Най­ди­те ко­си­нус внеш­не­го угла при вер­ши­не .

По­яс­не­ние.

так как

,

имеем

Ответ: –0,96.

Ответ: -0,96

4. B 15 . Най­ди­те пло­щадь за­кра­шен­ной фи­гу­ры на ко­ор­ди­нат­ной плос­ко­сти.

По­яс­не­ние.

Пло­щадь за­кра­шен­ной фи­гу­ры равна раз­но­сти пло­ща­ди боль­шо­го и ма­лень­ко­го ром­бов. Пло­щадь ромба равна по­ло­ви­не про­из­ве­де­ния его диа­го­на­лей. По­это­му

 

Ответ: 24.

Ответ: 24

5. B 15 . 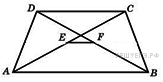Ос­но­ва­ния тра­пе­ции равны 3 и 2. Най­ди­те от­ре­зок, со­еди­ня­ю­щий се­ре­ди­ны диа­го­на­лей тра­пе­ции.

По­яс­не­ние.

От­ре­зок, со­еди­ня­ю­щий се­ре­ди­ны диа­го­на­лей тра­пе­ции равен по­лу­раз­но­сти боль­ше­го и мень­ше­го ос­но­ва­ний. По­это­му он равен (3 − 2):2 = 0,5.

 

Ответ: 0,5.

Ответ: 0,5

6. B 15 . 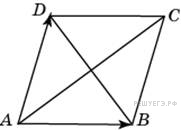Диа­го­на­ли изоб­ра­жен­но­го на ри­сун­ке ромба равны 12 и 16. Най­ди­те длину век­то­ра  + .

По­яс­не­ние.

Длина век­то­ра равна век­то­ру . Длина век­то­ра равна .

 

Ответ: 16.

Ответ: 16

7. B 15 . 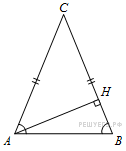В тре­уголь­ни­ке , вы­со­та равна 4, . Най­ди­те .

По­яс­не­ние.

Тре­уголь­ник рав­но­бед­рен­ный, зна­чит, углы и равны как углы при его ос­но­ва­нии.

 

Ответ: 0,5.

Ответ: 0,5

8. B 15 . Най­ди­те пло­щадь тре­уголь­ни­ка, вер­ши­ны ко­то­ро­го имеют ко­ор­ди­на­ты (0;0), (10;8), (8;10).

 

 

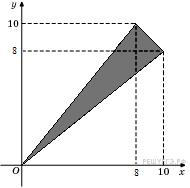
По­яс­не­ние.

Пло­щадь тре­уголь­ни­ка равна раз­но­сти пло­ща­ди пря­мо­уголь­ни­ка и трех пря­мо­уголь­ных тре­уголь­ни­ков. По­это­му

 

см².

Ответ: 18.

Ответ: 18

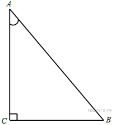
9. B 15 . В тре­уголь­ни­ке угол равен 90°, , . Най­ди­те .

По­яс­не­ние.

 

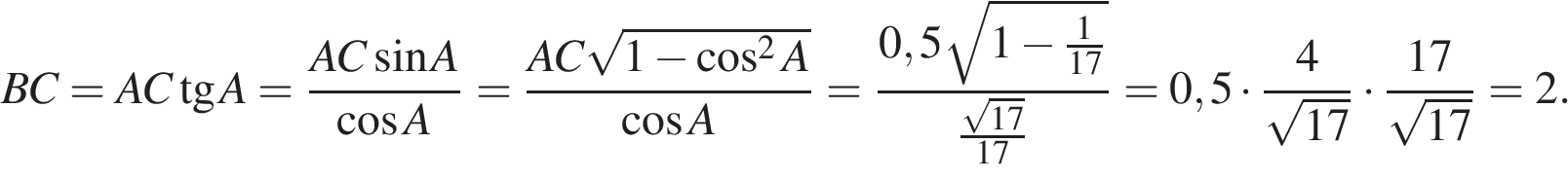
Ответ: 2.

Ответ: 2

10. B 15 . В тре­уголь­ни­ке , угол равен 90°. Ра­ди­ус опи­сан­ной окруж­но­сти этого тре­уголь­ни­ка равен 5. Най­ди­те .