
- •1. Проект, описание работ и отношений в проекте
- •2. Способы задания порядка выполнения работ в проекте
- •3. Характеристики времени в проекте (временные характеристики)
- •3.1. Временные характеристики событий и проекта
- •3.2. Временные характеристики работ
- •3.3. Последовательность работ, путь. Временные характеристики пути
- •4. Постановка задачи сетевого планирования
- •5. Расчёт временных характеристик в проекте
- •5.1. Расчет временных характеристик событий
- •5.2. Расчет временных характеристик работ
- •5.3. Расчет временных характеристик путей
- •5. 4. Построение сетевого графика критических работ проекта
5. 4. Построение сетевого графика критических работ проекта
Для анализа выполнения работ проекта в кратчайшие сроки используется сетевой график критических работ проекта или просто график критических работ. Сначала рекомендуется сделать эскиз графика критических работ. Для этого последовательно отмечают все критические события проекта в порядке их наступления. После этого последовательно наносятся критические работы проекта с помощью дуг, которые соединяют начало и окончание работы. Полученный эскиз проверяют на отсутствие тупиковых событий и связности графика, а также наличия циклов. В сетевом графике критических работ не должно быть событий, в которые не входит ни одна работа, кроме начального события. Также не должно быть событий, из которых не выходит ни одна работа, кроме конечного события. Для любого события должен быть путь, который проходит через данное событие, и соединяет начальное и конечное событие. Для каждого события не должно быть последовательности работ, которая начинается событием и заканчивается этим же событием.
На основе эскиза сетевого графика строится сам график, с проекциями критических событий на временную ось. Рекомендуется сетевой график строить так, чтобы два события, для которых есть критическая работа, соединялись этой работой горизонтально, а другие последовательности работ, соединяющие эти события, располагались выше данной работы. Это требование не обязательное, но иногда упрощает построение сетевого графика критических работ.
П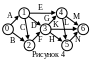 ример
1. Рассматривается проект. Для проекта
определён список работ A,
B, C, D,
E, F, G,
H, K, L,
M, N, которые
необходимо выполнить. Для каждой работы
определено время её выполнения в табл.
1. Порядок выполнения работ, задан сетевым
графиком, рис. 4.
ример
1. Рассматривается проект. Для проекта
определён список работ A,
B, C, D,
E, F, G,
H, K, L,
M, N, которые
необходимо выполнить. Для каждой работы
определено время её выполнения в табл.
1. Порядок выполнения работ, задан сетевым
графиком, рис. 4.
1. Определить временные характеристики событий и критическое время проекта, критические события. 2. Найти полные резервы времени работ, критические работы. 3. Построить сетевой график критических работ проекта.
Продолжительности работ проекта Таблица 1
Работа |
A |
B |
C |
D |
E |
F |
G |
H |
K |
L |
M |
N |
Продолжительность работы |
7 |
11 |
4 |
8 |
15 |
6 |
9 |
13 |
16 |
3 |
5 |
2 |
Решение. 1. Рассчитаем временные
характеристики событий и критическое
время проекта. В задаче не оговорено,
что проект начинается в заданный момент
времени, поэтому полагаем, что раннее
время начального события равняется
нулю. Начальным событием является
нулевое событие, поэтому
![]() =
=0.
=
=0.
 Дальше
определим раннее время первого события,
так как ему предшествует событие 0,
раннее время которого мы уже определили.
В событие 1 входит одна работа – это
работа А. Началом работы А является
событие 0 (рис. 5). Вычислим для работы А
сумму раннего времени события 0 и
продолжительности работы А:
+
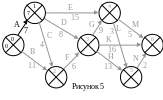
Дальше
определим раннее время первого события,
так как ему предшествует событие 0,
раннее время которого мы уже определили.
В событие 1 входит одна работа – это
работа А. Началом работы А является
событие 0 (рис. 5). Вычислим для работы А
сумму раннего времени события 0 и
продолжительности работы А:
+![]() =0+7=7.
Раннее время события 1 равняется значению
этой суммы:
=0+7=7.
Раннее время события 1 равняется значению
этой суммы:
![]() =7.
Это значение отметим на графике в левом
секторе события 1 (рис. 5).
=7.
Это значение отметим на графике в левом
секторе события 1 (рис. 5).
 Теперь
можно рассчитать раннее время события
2, так как ему предшествуют событие 0 и
событие 1. Раннее время события 3 ещё
нельзя рассчитать, так как не известно
значение раннего времени события 2,
которое предшествует событию 3. В событие
2 входят две работы: работа В и работа
С. Началом работы В является событие 0,
а работы С событие 1 (рис. 6). Для каждой
из работ рассчитываем сумму раннего
времени работы и продолжительности
работы. Для работы В сумма равна:
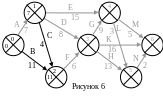
Теперь
можно рассчитать раннее время события
2, так как ему предшествуют событие 0 и
событие 1. Раннее время события 3 ещё
нельзя рассчитать, так как не известно
значение раннего времени события 2,
которое предшествует событию 3. В событие
2 входят две работы: работа В и работа
С. Началом работы В является событие 0,
а работы С событие 1 (рис. 6). Для каждой
из работ рассчитываем сумму раннего
времени работы и продолжительности
работы. Для работы В сумма равна:
![]() +
+![]() =0+11=11.
Для работы С получаем сумму
+
=0+11=11.
Для работы С получаем сумму
+![]() =7+4=11.
Раннее время события 2 равняется
наибольшему значению из полученных
сумм:
=7+4=11.
Раннее время события 2 равняется
наибольшему значению из полученных
сумм:
![]() =
=![]() =11.
На графике записываем значение раннего
времени события 2 в левом секторе события
2 (рис. 6).
=11.
На графике записываем значение раннего
времени события 2 в левом секторе события
2 (рис. 6).
 Далее
рассчитываем раннее время события 3.
Раннее время событий 4 и 5 рассчитать
нельзя, так как им предшествует событие
3, для которого раннее время ещё не
рассчитано. В событие 3 входят две работы,
работа D и работа F.
Началом работы D будет
событие 1, а работы F событие
2. Рассчитываем суммы для этих работ.
Для работы :
+
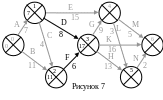
Далее
рассчитываем раннее время события 3.
Раннее время событий 4 и 5 рассчитать
нельзя, так как им предшествует событие
3, для которого раннее время ещё не
рассчитано. В событие 3 входят две работы,
работа D и работа F.
Началом работы D будет
событие 1, а работы F событие
2. Рассчитываем суммы для этих работ.
Для работы :
+![]() =7+8=15;
для работы :
+
=7+8=15;
для работы :
+![]() =11+6=17.
Раннее время события 3 равняется
наибольшему значению из найденных
значений сумм:
=11+6=17.
Раннее время события 3 равняется
наибольшему значению из найденных
значений сумм:
![]() =
=![]() =17.
На графике отмечаем раннее время события
3 в его левом секторе (рис. 7).
=17.
На графике отмечаем раннее время события
3 в его левом секторе (рис. 7).
С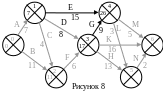 ейчас
можно рассчитать ранее время события
4, но нельзя рассчитать раннее время
событий 5 и 6. В событие 4 входят две
работы, работа E, которая
начинается событием 1, и работа G,
которая начинается событием 3. Рассчитываем
суммы для этих работ. Для работы E:
+
ейчас
можно рассчитать ранее время события
4, но нельзя рассчитать раннее время
событий 5 и 6. В событие 4 входят две
работы, работа E, которая
начинается событием 1, и работа G,
которая начинается событием 3. Рассчитываем
суммы для этих работ. Для работы E:
+![]() =7+15=22;
для G:
+
=7+15=22;
для G:
+![]() =17+9=26.
Раннее время события 4 равно:
=17+9=26.
Раннее время события 4 равно:
![]() =
=![]() =26.
Отмечаем на графике в левом секторе
раннее время события 4 (рис. 8).
=26.
Отмечаем на графике в левом секторе
раннее время события 4 (рис. 8).
 Рассчитываем
раннее время события 5. В это событие
входят работы H и L.
Они начинаются событиями 3 и 4. Для работы
H сумма равна:
+
Рассчитываем
раннее время события 5. В это событие
входят работы H и L.
Они начинаются событиями 3 и 4. Для работы
H сумма равна:
+![]() =17+13=30;
для работы L:
+
=17+13=30;
для работы L:
+![]() =26+3=29.
Тогда
=26+3=29.
Тогда
![]() =
=![]() =30.
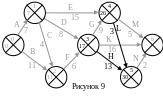
На графике отмечаем раннее время события
5 (рис. 9).
=30.
На графике отмечаем раннее время события
5 (рис. 9).
Т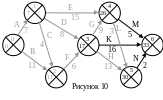 еперь
можно рассчитать раннее время события
6, которое является конечным. В событие
6 входят работы K, M
и N. Они начинаются событиями
3, 4 и 5. Вычислим суммы для этих работ.
Для работы K сумма равна:
+
еперь
можно рассчитать раннее время события
6, которое является конечным. В событие
6 входят работы K, M
и N. Они начинаются событиями
3, 4 и 5. Вычислим суммы для этих работ.
Для работы K сумма равна:
+![]() =17+16=33.
Для работы M:
+
=17+16=33.
Для работы M:
+![]() =
=26+5=31. Для работы N:
+
=
=26+5=31. Для работы N:
+![]() =30+2=32.
Раннее время конечного события равно
=
=30+2=32.
Раннее время конечного события равно
=![]() =
=![]() =33.
=33.
Определяем критическое время проекта. Оно равняется раннему времени конечного события: = =33.
Переходим к расчёту позднего времени
наступления событий. Позднее время
конечного события равняется критическому
времени проекта:
=
=33.
Так как конечным является событие 6, то
позднее время события 6 тоже равняется
33:
![]() =33.
Позднее время события 6 записываем на
графике в правом секторе события 6 (рис.
11).
=33.
Позднее время события 6 записываем на
графике в правом секторе события 6 (рис.
11).
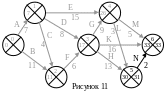 Последовательно
найдём позднее время остальных событий,
начиная с конечного и заканчивая
начальным. Зная позднее время события
6, можно определить позднее время события
5. Находим на графике работы, которые
выходят из события 5 и окончания этих
работ. Из события 5 выходит работа N,
которая заканчивается событием 6. Для
этой работы находим разность позднего
времени события 6 и продолжительности
работы:
Последовательно
найдём позднее время остальных событий,
начиная с конечного и заканчивая
начальным. Зная позднее время события
6, можно определить позднее время события
5. Находим на графике работы, которые
выходят из события 5 и окончания этих
работ. Из события 5 выходит работа N,
которая заканчивается событием 6. Для
этой работы находим разность позднего
времени события 6 и продолжительности
работы:
 –
=33–2=31.
Позднее время события 5 равняется этой
разности:
–
=33–2=31.
Позднее время события 5 равняется этой
разности:
![]() =31.
Позднее время события 5 отмечаем на
графике в правом секторе этого события
(рис. 11).
=31.
Позднее время события 5 отмечаем на
графике в правом секторе этого события
(рис. 11).
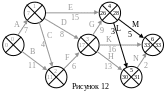
Рассчитаем позднее время события 4. На
сетевом графике находим все работы,
выходящие из события 4 (рис. 12). Это работы
L и M, которые
заканчиваются событиями 5 и 6 соответственно.
Для каждой из работ находим разность
позднего времени окончания работы и
продолжительности работы. Для работы
L эта разность равна:
–
=31–3=28.
Для работы M разность
принимает значение:
–
=33–5=28.
Наименьшее значение из найденных
разностей равняется 28. Позднее время
события 4 равно:
![]() =
=![]() =28.
Позднее время события 4 отмечаем на
сетевом графике в правом секторе события
4.
=28.
Позднее время события 4 отмечаем на
сетевом графике в правом секторе события
4.
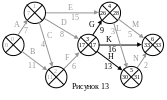 Теперь
можно рассчитать позднее время события
3, так как позднее время событий, следующих
за событием 3 (события 4, 5 и 6) уже рассчитаны.
Находим работы, которые выходят из
события 3. Это работы G, K
и H (рис. 13). Они заканчиваются
соответственно событиями 4, 6 и 5. Для
найденных работ находим значения
разностей: для работы G –
–
=28–9=19,
для работы K –
–
=31–13=18,
для работы H –
–
=33–16=17.
Позднее время события 3 равняется
наименьшему значению из найденных
разностей:
Теперь
можно рассчитать позднее время события
3, так как позднее время событий, следующих
за событием 3 (события 4, 5 и 6) уже рассчитаны.
Находим работы, которые выходят из
события 3. Это работы G, K
и H (рис. 13). Они заканчиваются
соответственно событиями 4, 6 и 5. Для
найденных работ находим значения
разностей: для работы G –
–
=28–9=19,
для работы K –
–
=31–13=18,
для работы H –
–
=33–16=17.
Позднее время события 3 равняется
наименьшему значению из найденных
разностей:
![]() =
=![]() =17.
Позднее время события 3 отмечаем в правом
секторе этого события (рис. 13).
=17.
Позднее время события 3 отмечаем в правом
секторе этого события (рис. 13).
Рассчитываем позднее время события 2.
Из него выходит работы F.
Она заканчивается событием 3. Разность
для работы F равна:
–
=17–6=11.
Позднее время события 2 равно
![]() =11
(рис. 14).
=11
(рис. 14).
Позднее время события 1 равняется минимальной разности для работ E, D и C:
![]() =
=![]() =7
(рис. 15).
=7
(рис. 15).
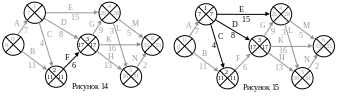 Осталось
определить позднее время события 0. Из
события 0 выходят работы А и В (рис. 16).
Для них значения разностей равны:
–
=11–11=0,
–
=7–7=0.
Позднее время события 0 равно:
Осталось
определить позднее время события 0. Из
события 0 выходят работы А и В (рис. 16).
Для них значения разностей равны:
–
=11–11=0,
–
=7–7=0.
Позднее время события 0 равно:
![]() =
=![]() =0.
Так как событие 0 является начальным
событием, то данные расчёт будет
контрольным. Для начального события
позднее время равняется 0. В противном
случае при вычислениях допущена ошибка.
Контрольное вычисление показало, что
=0.
=0.
Так как событие 0 является начальным
событием, то данные расчёт будет
контрольным. Для начального события
позднее время равняется 0. В противном
случае при вычислениях допущена ошибка.
Контрольное вычисление показало, что
=0.
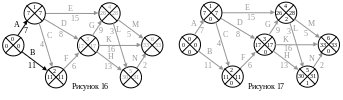 Для событий осталось рассчитать резервы
времени событий, которые мы запишем в
нижних секторах этих событий. Резерв
времени события равен разности позднего
и раннего времени события. Найдём резервы
времени событий и отметим их на сетевом
графике (рис. 17).
Для событий осталось рассчитать резервы
времени событий, которые мы запишем в
нижних секторах этих событий. Резерв
времени события равен разности позднего
и раннего времени события. Найдём резервы
времени событий и отметим их на сетевом
графике (рис. 17).
![]() =
–
=0–0=0;
=
–
=0–0=0;
![]() =
–
=7–7=0;
=
–
=7–7=0;
![]() =
–
=11–11=0;
=
–
=11–11=0;
![]() =
–
=
–
–
=17–17=0;
![]() =
–
=28–26=2;
=
–
=28–26=2;
![]() =
–
=31–30=1;
=
–
=31–30=1;
![]() =
–
=33–33=0.
=
–
=33–33=0.
Выпишем критические события: 0, 1, 2, 3, 6.
2. Рассчитаем полные резервы работ. Для
расчёта можно использовать таблицу. В
этой таблице представим работу в виде
пары событий, определим раннее время
начала работы и позднее время окончания
работы, выпишем время выполнения работы
и рассчитаем полный резерв времени
работы (табл. 2). Полный резерв времени
работы вычисляем по формуле:
=
–
–
.
Например, рассчитаем полный резерв
времени работы D, которую
можно представить как пару событий
(1;3).
![]() =
=![]() =
–
–
=
–
–![]() =
=
=17–7–8=2. Это работа некритическая.
Поэтому в последней строке её помечать
не будем. Рассчитаем полный резерв
времени работы F. F
=(2;3).
![]() =
=![]() =
=![]() –
–
–
–![]() =
17–11–6=0. Это работа критическая. Поэтому
в последней строке её пометим буквой
к.
=
17–11–6=0. Это работа критическая. Поэтому
в последней строке её пометим буквой
к.
Расчёт полного резерва времени работы Таблица 2
Название работы, |
A |
B |
C |
D |
E |
F |
G |
H |
K |
L |
M |
N |
Представление работы в виде пары событий, |
(0;1) |
(0;2) |
(1;2) |
(1;3) |
(1;4) |
(2;3) |
(3;4) |
(3;5) |
(3;6) |
(4;5) |
(4;6) |
(5;6) |
Раннее время начала работы, |
0 |
0 |
7 |
7 |
7 |
11 |
17 |
17 |
17 |
26 |
26 |
30 |
Позднее время окончания работы, |
7 |
11 |
11 |
17 |
28 |
17 |
28 |
31 |
33 |
31 |
33 |
33 |
Продолжительность работы, |
7 |
11 |
4 |
8 |
15 |
6 |
9 |
13 |
16 |
3 |
5 |
2 |
Полный резерв времени работы, |
0 |
0 |
0 |
2 |
6 |
0 |
2 |
1 |
0 |
2 |
2 |
1 |
Отметка о виде работы |
к |
к |
к |
|
|
к |
|
|
к |
|
|
|
В последней строке делаем пометку, если работа критическая, то ставим букву к.
По таблице выписываем критические работы: A, B, C, F, K.
3. Построим сетевой график критических работ проекта.
С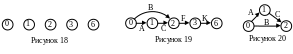 начала
построим эскиз сетевого графика.
Последовательно отметим на эскизе все
критические события. В нашей задаче,
это события 0, 1, 2, 3 и 6 (рис. 18). Потом
соединим нанесённые события критическими
работами A, B,
C, F и K
(рис. 19). Преобразуем эскиз следующим
образом. Если из одного события в другое
событие есть несколько последовательностей
работ, то напрямую связываем события
наиболее короткой последовательностью.
Например, из события 0 в событие 2 можно
попасть через событие 1, с помощью работ
A и C, и
напрямую, через работу B.
Тогда на сетевом графике горизонтально
строим работу В, соединяющую события 0
и 2, а выше строим с помощью работ A
и C последовательность
работ, проходящую через событие 1(рис.
20). Все остальные последовательности,
соединяющие события 2 и 3, 3 и 6 , рисуем
горизонтально. Далее полученный сетевой
график проецируем на временную ось,
помечая моменты времени критических
событий (рис. 21). Таким образом, получаем
сетевой график критических работ и
путей.
начала
построим эскиз сетевого графика.
Последовательно отметим на эскизе все
критические события. В нашей задаче,
это события 0, 1, 2, 3 и 6 (рис. 18). Потом
соединим нанесённые события критическими
работами A, B,
C, F и K
(рис. 19). Преобразуем эскиз следующим
образом. Если из одного события в другое
событие есть несколько последовательностей
работ, то напрямую связываем события
наиболее короткой последовательностью.
Например, из события 0 в событие 2 можно
попасть через событие 1, с помощью работ
A и C, и
напрямую, через работу B.
Тогда на сетевом графике горизонтально
строим работу В, соединяющую события 0
и 2, а выше строим с помощью работ A
и C последовательность
работ, проходящую через событие 1(рис.
20). Все остальные последовательности,
соединяющие события 2 и 3, 3 и 6 , рисуем
горизонтально. Далее полученный сетевой
график проецируем на временную ось,
помечая моменты времени критических
событий (рис. 21). Таким образом, получаем
сетевой график критических работ и
путей.
В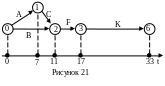 литературе по-разному изображается
график выполнения критических работ.
Здесь предлагается такой сетевой график,
чтобы показать, что это математическая
модель графика выполнения критических
работ, так как задача решается
математическими методами. На основе
этого сетевого графика специалист
определяет своё представление о
выполняемых работах, удобное для его
восприятий и его реализации.
литературе по-разному изображается
график выполнения критических работ.
Здесь предлагается такой сетевой график,
чтобы показать, что это математическая
модель графика выполнения критических
работ, так как задача решается
математическими методами. На основе
этого сетевого графика специалист
определяет своё представление о
выполняемых работах, удобное для его
восприятий и его реализации.
1.Исследование операций в экономике: Учебн. Пособие для Вузов/ под ред. проф. Н. Ш. Кремера. — М.:ЮНИТИ,2010. — 407 с.
2.Экономико-математические методы и прикладные модели:учеб. пособие для студ. вузов по экон. спец./ под ред. В.В. Федосеева. — М.:ЮНИТИ,2002. — 391 с.
3.Федосеев В.В. Экономико-математические методы и модели в маркетинге: учеб, пособие для студ. вузов по спец. "Маркетинг"/ В.В. Федосеев, Н.Д. Эриашвили; под ред. В.В. Федосеева. —2-е изд., перераб. и доп. — М.:Юнити,2001. — 159 с. — Библиогр.: с. 156-157.
