2.2. Решающие деревья

Решающее дерево (decision tree, DT) — это логический алгоритм клас­сификации, основанный на поиске конъюнктивных закономерностей.

Напомним некоторые понятия теории графов.

Деревом называется конечный связный граф с множеством вершин V, не со­держащий циклов и имеющий выделенную вершину 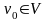, в которую не входит ни одно ребро. Эта вершина называется корнем дерева. Вершина, не имеющая выхо­дящих рёбер, называется терминальной или листом. Остальные вершины называ­ются внутренними.

Дерево называется бинарным, если из любой его внутренней вершины выхо­дит ровно два ребра. Выходящие рёбра связывают внутреннюю вершину v с левой дочерней вершиной L_v и с правой дочерней вершиной R_v.

Опр. Бинарное решающее дерево — это алгоритм классификации, задающийся бинарным деревом, в котором каждой внутренней вершине 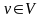приписан предикат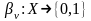 , каждой терминальной вершине приписано имя класса c_v Y. Правило классификации определяется следующим образом:

Алгоритм :Классификация объекта х X бинарным решающим деревом

1: v:=v₀;

2: пока вершина v внутренняя

3: если 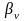(x) то

4: v := R_v;

5: иначе

6: v := L_v-

7: вернуть c_v.

2.3. Редукция решающих деревьев

Суть редукции состоит в удалении поддеревьев, имеющих недостаточную ста­тистическую надёжность. При этом дерево перестаёт безошибочно классифициро­вать обучающую выборку, зато качество классификации новых объектов (способ­ность к обобщению), как правило, улучшается.

Придумано огромное количество эвристик для проведения редукции , однако ни одна из них, вообще говоря, не гарантирует улучшения качества классификации.

Предредукция (pre-pruning) или критерий раннего останова досрочно прекра­щает дальнейшее ветвление в вершине дерева, если информативность I(β, S) для всех предикатов 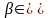Β не дотягивает до заданного порогового значения I₀.

Предредукция не является эффективным методом избежания переобучения, так как жадное ветвление по-прежнему остаётся глобально неоптимальным. Более эффективной считается стратегия постредукции.

Постредукция (post-pruning) просматривает все внутренние вершины дерева и заменяет отдельные вершины либо одной из дочерних вершин (при этом вторая дочерняя удаляется), либо терминальной вершиной. Процесс замен продолжается до тех пор, пока в дереве остаются вершины, удовлетворяющие критерию замены.

Критерием замены является сокращение числа ошибок на контрольной выбор­ке, отобранной заранее и не участвовавшей в обучении дерева. Рекомендуется остав­лять в контроле около 30% объектов. Наиболее экономичной реализацией постре­дукции является просмотр дерева методом поиска в глубину, при котором в каждой вершине дерева сохраняется информация о подмножестве контрольных объектов, попавших в данную вершину при классификации.

3. Описание алгоритмов построения деревьев решений

3.1. Алгоритм id3

Идея алгоритма заключается в последовательном дроблении выборки на две части до тех пор, пока в каждой части не окажутся объекты только одного класса. Проще всего записать этот алго­ритм в виде рекурсивной процедуры LearnID3, которая строит дерево по заданной подвыборке S. Для построения полного дерева она применяется ко всей выборке и возвращает указатель на корень построенного дерева:

v₀ := LearnID3 (X^l).

На шаге 6 алгоритма выбирается предикат β, задающий максимально ин­формативное ветвление дерева — разбиение выборки на две части S = s₀ U S₁. На практике применяются различные критерии ветвления.

1. Критерий, ориентированный на скорейшее отделение одного из классов.

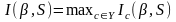
2. Критерий, ориентированный на задачи с большим числом классов. Фактиче­ски, это обобщение статистического определения информативности.

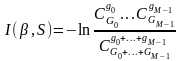,где

G_c-число объектов класса с в выборке S, из них g_c объектов покрываются правилом β.

3. D-критерий — число пар объектов из разных классов, на которых предикат β принимает разные значения. В случае двух классов он имеет вид

I(β,S)=g(β)(B-b(β))+b(β)(G-g(β)).

Трудоёмкость алгоритма ID3 составляет O(|B|Vol), где v₀ — число внутренних вершин дерева.

Алгоритм :Рекурсивный алгоритм построения решающего дерева ID3 Вход:

S — обучающая выборка;

В — множество базовых предикатов;

Выход:

Возвращает корневую вершину дерева, построенного по выборке S;

1: ПРОЦЕДУРА LearnID3 (S);

2: если все объекты из S лежат в одном классе с Y то

3: создать новый лист v;

_{4: cv:=c;}

5: вернуть (v);

6: найти предикат с максимальной информативностью:

β:= arg ;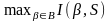

7: разбить выборку на две части S = 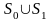по предикату β:

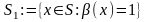
8: если 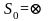или то

9: создать новый лист v;

10:c_v := класс, в котором находится большинство объектов из S;

11: вернуть (v);

12: иначе

13: создать новую внутреннюю вершину v;

14: β_v:= β;

15: L_v := LearnID3 (So); (построить левое поддерево)

16: R_v := LearnID3 (S₁); (построить правое поддерево)

17: вернуть (v);

Преимущества алгоритма ID3

-Простота и интерпретируемость классификации. Алгоритм способен не только классифицировать объект, но и выдать объяснение классификации в терминах предметной области. Для этого достаточно записать последователь­ ность условий, пройденных объектом от корня дерева до листа.

-Алгоритм синтеза решающего дерева имеет сложность, линейную по длине выборки.

-Если множество предикатов В настолько богато, что на шаге 6 всегда нахо­дится предикат, разбивающий выборку S на непустые подмножества s₀ и S₁,то алгоритм строит бинарное решающее дерево, безошибочно классифицирую­ щее выборку X^l.

-Алгоритм очень прост для реализации и легко поддаётся различным усовер­шенствованиям. Можно использовать различные критерии ветвления и крите­рии останова, вводить редукцию, и т. д.

Недостатки алгоритма ID3

-Жадность. Локально оптимальный выбор предиката β_V не является глобально оптимальным. В случае выбора неоптимального предиката алгоритм не спосо­ бен вернуться на уровень вверх и заменить неудачный предикат.

-Чем дальше вершина v расположена от корня дерева, тем меньше длина подвыборки S, по которой приходится принимать решение о ветвлении в вершине v. Тем менее статистически надёжным является выбор предиката β_V.

-Алгоритм склонен к переобучению — как правило, он переусложняет структуру дерева. Обобщающая способность алгоритма (качество классификации новыхобъектов) относительно невысока.

Основная причина недостатков — неоптимальность жадной стратегии наращи­вания дерева. Перечисленные недостатки в большей или меньшей степени свойствен­ны большинству алгоритмов синтеза решающих деревьев. Для их устранения при­меняют различные эвристические приемы: редукцию, элементы глобальной оптими­зации, «заглядывание вперёд» (look ahead).