Уравнение неразрывности потока

Рассмотрим зависимость между скоростями в потоке жидкости при условии неразрывности движения*.

Для этого выделим внутри потока элементарный параллелепи­пед, объем которого dV= dxdydz (рис.6). Составляющую скорос­ти вдоль оси х обозначим v_х. Тогда через левую грань параллеле­пипеда площадью dydz в него войдет за бесконечно малый проме­жуток времени масса жидкости, равная

М_х = ρv_xdydzdτ,

где р — плотность жидкости.

Примем допущение, что жидкость несжимаема. Тогда плот­ность жидкости ρ в потоке постоянна.

* Условие неразрывности соблюдается, когда в потоке жидкости не образуют­ся пустоты, не заполненные жидкостью.

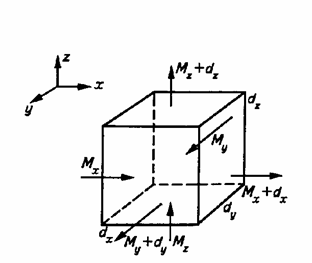
Рис. 4.6. К выводу уравнения неразрывности потока жидкости

Равномерное движение наблюдается, когда скорость, давление, глубина и форма потока не меняются по его длине. Примером равномерного движения является движение жидкости в трубопро­воде постоянного сечения с постоянной скоростью.

Неравномерное движение происходит, например, в коничес­кой трубе, когда скорость, давление и глубина потока изменяются по длине трубы.

Если рассмотреть поперечное сечение потока жидкости и мыс­ленно представить его состоящим из отдельных элементарных струек, то окажется, что частицы жидкости, которые находятся в струйках, расположенных на различном расстоянии от оси пото­ка, движутся с различными скоростями.

Скорость движения жидкости будет максимальной по оси по­тока и минимальной в струйках у стенки трубы. Распределение скоростей в потоке зависит от режима движения жидкости.

В технике оперируют не локальными скоростями частиц жид­кости, а средней скоростью потока.

Эта скорость представляет собой отношение секундного объем­ного расхода V_ceк к площади поперечного сечения потока F:

v = V_ceк / F, (4.1.)

откуда V_ceк =vF, а массовый расход, кг/с,

G = ρvF, где ρ — плотность жидкости, кг/м³.

При движении жидкости через поперечное сечение, отличное от круглого, в качестве расчетного линейного размера принимают гидравлический радиус или эквивалентный диаметр.

Гидравлический радиус вычисляют как отношение площади свободного сечения трубопровода или канала к смоченному пери­метру

r= F / П, (4.2)

где F — площадь сечения потока, м².

11.Уравнение Бернулли для потока реальной жидкости

В реальных потоках жидкости присутствуют силы вязкого трения. В результате слои жидкости трутся друг об друга в процессе движения. На это трение затрачивается часть энергии потока. По этой причине в процессе движения неизбежны потери энергии. Эта энергия, как и при любом трении, преобразуется в тепловую энергию. Из-за этих потерь энергия потока жидкости по длине потока, и в его направлении постоянно уменьшается. Т.е. напор потока H_потока в направлении движения потока становится меньше. Если рассмотреть два соседних сечения 1-1 и 2-2, то потери гидродинамического напора Δh составят:

,

где H_1-1- напор в первом сечении потока жидкости,

H_2-2 - напор во втором сечении потока,

∆h - потерянный напор - энергия, потерянная каждой единицей веса движущейся жидкости на преодоление сопротивлений на пути потока от сечения 1-1 до сечения 2-2.

С учётом потерь энергии уравнение Бернулли для потока реальной жидкости будет выглядеть

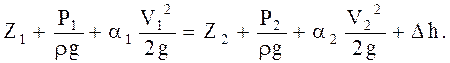
Индексами 1 и 2 обозначены характеристики потока в сечениях 1-1 и 2-2.

Если учесть, что характеристики потока V и α зависят от геометрии потока, которая для напорных потоков определяется геометрией трубопровода, понятно, что потери энергии (напора) в разных трубопроводах будут изменяться неодинаково. Показателем изменения напора потока является гидравлический уклонI, который характеризует потери напора на единице длины потока. Физический смысл гидравлического уклона – интенсивность рассеяния энергии по длине потока. Другими словами, величина I показывает, как быстро трубопровод поглощает энергию потока, протекающего в нём

.

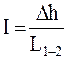Изменение энергии по длине потока удобно проследить на графиках. Из уравнения Бернулли для потока реальной жидкости (закона сохранения энергии) видно, что гидродинамическая линия для потока реальной жидкости (с одним источником энергии) всегда ниспадающая. То же справедливо и для пьезометрической линии, но только в случае равномерного движения, когда скоростной напор 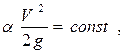а уменьшение напора происходит только за счёт изменения потенциальной энергии потока, главным образом за счёт уменьшения давления P.

Пьезометрическим уклоном называют изменение удельной потенциальной энергии жидкости вдоль потока, приходящееся на единицу его длины.

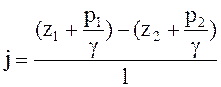
Если гидравлический уклон всегда положителен, то пьезомет­рический может быть и положительным, и отрицательным. При равномерном движении жидкости, когда скорость по длине потока не изменяется, скоростной напор вдоль потока av² / (2g) = const. Следовательно, пьезометрическая линия параллельна энергети­ческой, и пьезометрический уклон равен гидравлическому.

Изменение удельной потенциальной энергии положения вдоль потока жидкости, приходящееся на единицу длины, назы­вают геометрическим уклоном i и определяют по формуле

Рассматривая уравнение Бернулли для установив­шегося движения элементарной струйки идеальной жидкости, выделим в потоке жидкости элементарную струйку и определим удельную энергию жидкости. В идеальной жидкости при движе­нии не возникает сила трения, поэтому на основании закона сохранения энергии E₁=E₂.

Уравнение Бернулли для элементарной струйки идеальной жидкости имеет вид

Здесь с энергетической точки зрения (в единицах энергии, Дж/кг) gz — удель­ная потенциальная энергия положения; Р/r — удельная потенциальная энергия давления; gz + Р/r — удельная потенциальная энергия; u²/2 — удельная кинети­ческая энергия; и — скорость элементарной струйки идеальной жидкости.

Энергетический смысл уравнения Бернулли: для элементар­ной струйки идеальной жидкости полная удельная энергия, рав­ная сумме удельной потенцальной энергии давления, удельной потенциальной энергии положения и кинетической удельной потенциальной энергии положения и кинетической удельной энергии, есть величина постоянная во всех сечениях по отноше­нию к выбранной плоскости отсчета.

Разделив уравнение на g, получим уравнение полного напора:

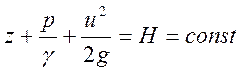
z - геометрическая высота или геометрический напор, м; P/g — пьезометрический напор или пьезометрическая высота, м; u²/(2g) —скоростной напор или скоростная высота, м; Н—полный напор, м.

Представим элементарную струйку идеальной жидкости с осью, проходящей через точки А, В и С (рис. а).

Рис. а .Графическая иллюстрация уравнения Бернулли для струйки идеальной жидкости

Точки А, В и С лежащие соответственно в сечениях 1—1, 2—2, 3—3, расположены на высоте z₁, z₂, z₃ над плоскостью сравнения О—О. Отложим от точки А вверх по вертикали отрезок АА₁, равный пьезометрической высоте Р₁/(rg), а затем от точки А₁ вверх отрезок A₁A₂, равный u²/(2g), т. е. равный скоростному напору. Аналогичное построение проведем для точек В, С в сечениях 2—2, 3-3. Такое же построение можно повторить и для остальных точек оси элементарной струйки. Вершины полученных вертикальных отрезков АА₂, ВВ₂, СС₂ и т. д. должны находиться на одинаковой высоте от плоскости сравнения, т. е. должны лежать в одной горизонтальной плоскости 0'— 0', так как сумма трех членов

z+ Р/r)+ u²/(2g) согласно уравнению ( ) вдоль всей . Струйки невязкой жидкости постоянна.

Для каждого сечения элементарной струйки полный напор Н это совокупность отрезков z ,Р/r) , u²/(2g). Соединив между собой концы отрезков Н, получим горизонтальную линию, которая называется линией полного напора. Линию изменения пьезометрических высот называют пьезометрической линией.

С геометрической точки зрения для движущейся идеальной жидкости уравнение Бернулли показывает, что сумма трех высот — геометрической, пьезометрической и скоростной — есть величина постоянная. Линия полного напора параллельна плоскости отсчета.

Умножив все члены уравнения ( ) на удельный вес жидкости g, получим

gz - весовое давление, Па; P — гидродинамическое давление, Па; rи² /2— динамическое давление Па; gH— полное давление, Па.

 

Уравнение Бернулли для элементарной струйки реальной жидкости (рис. б):

 

 

 

Рис.в.Графическая иллюстрация уравнения Бернулли для потока жидкости

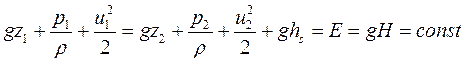
где ghs - потерянная удельная энергия, Дж/кг, затраченная на преодоление сопротивлений движению, обусловленных трением в вязкой жидкости.

Остальные члены уравнения имеют то же значение, что и в уравнении для идеальной жидкости.

При рассмотрении движения струйки реальной (вязкой) жидкости гидродинамический напор в каждом предыдущем сечении будет больше гидродинамического напора в последующем сече­нии на величину потерь напора hs. Соответственно с этим напорная плоскость или силовая линия 0' - 0' оказывается наклонной (рис. 3.2, б).

Вторая форма записи уравнения для струйки реальной жидкости:

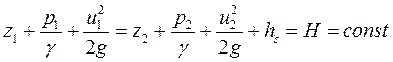
где с геометрической точки зрения ghs —потеря напора, м.

Линия полного напора представляет собой спадающую кри­вую.