5.Давление жидкости на плоскую стенку

Задача определения сил давления жидкости на плоскую стенку заключается в определении равнодействующей P сил давления (рис.7.1) на плоскую стенку, ее направления и точки приложения.

Рис. 7.1. Силы, действующие на плоскую стенку

Рассмотрим вертикальную прямоугольную стенку. Пусть ширина стенки равна B, уровень жидкости в сосуде H, а площадь смоченной поверхности рассматриваемой стенки равна S = BH.

Из основного уравнения гидростатики, записанного применительно к избыточному давлению любой точки жидкости,

p_изб = rgh. (7.1)

следует, что эпюра давления p_изб представляет собой прямоугольный треугольник. Причем максимальное избыточноедавление на стенку равно давлению на дно сосуда

p_max = rgH, (7.2)

а давление на уровне центра тяжести плоской стенки (точка С) равно

p_c= 0,5p_max= 0,5rgH, (7.3)

Учитывая переменный характер давления жидкости по высоте, выделим на текущей глубине h элементарную площадку dS= Bdh и определим элементарную силу давления жидкости на эту площадку

dP= pdS= rghBdh.

Для определения силы давления на всю смоченную поверхность полученное выражение проинтегрируем от 0 до H:

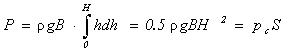(7.4)

где p_c-давление жидкости в центре тяжести (точка С) смоченной поверхности, определяемое по формуле (7.3); S-площадь смоченной поверхности (S=BH).

Формула (7.4) справедлива для плоских стенок любой формы и с любым углом наклона стенки к горизонту.

Очевидно, что направление действия равнодействующей для плоской стенки всегда совпадает с направлением элементарных сил гидростатического давления. Так как эти силы всегда нормальны к плоской стенке, то и равнодействующая сила будет также нормальной.

Точка приложения равнодействующей силы давления p называется центром давления. Центр давления (точка О) в общем случае не совпадает с центром тяжести плоской стенки (точка С) и находится на глубине, соответствующей расположению центра тяжести площади эпюры давлений (см. рис. 7.1). В рассматриваемом случае центр давления находится на глубине

h_o= 2/3H.

Если рассматривать дно сосуда, центр тяжести и центр давления совпадают.

6.Сила давления жидкости на криволинейные поверхности

Выделим на некоторой цилиндрической поверхности АВ (рис. 9) элементарную площадку с центром тяжести, погруженным на глуби­ну h под свободную поверхность жидкости. Если давление на по­верхности жидкости равно р₀, то гидростатическое (абсолютное) давление в центре тяжести площадки составит

р=р_{0 +} .

Тогда dР − элементарная сила абсолютного гидростатического давления на площадку будет равна

dP = (p₀ + ) (2.33)

и направлена по нормали к ней, проведенной через центр тяжести.

Рис.9

Разложим элементарную силу абсолютного гидростатического давления на вертикальную и горизонтальную составляющие, обозна­чив угол между элементарной силой dP и вертикалью через :

(2.34)

где ·cos = _xoy − площадь проекции на плоскость XOY; ·sin = _zoy − площадь проекции на плоскость ZOY.

С учетом приведенных выше равенств уравнение (2.34) можно записать в виде:

(2.35)

Если всю поверхность АВ разбить на ряд элементарных площа­док и для каждой из них определить значения dP_В и dP_Г, то вертикальную Р_В и горизонтальную Р_Г составляющие силы абсолютного гидростатического давления жидкости Р на цилиндрическую поверхность АВ можно найти суммированием всех элементарных сил dP_В и dP_Г или интегрированием уравнений (2.35):

(2.36)

. (2.37)

Первые интегралы в уравнениях (2.36) и (2.37) равны соответственно площадям проекций цилиндрической поверхности АВ на горизонтальную XOY и вертикальную ZOY плоскости, т.е.

, а .

Проведя вертикальные образующие через различные точки пара­метра элементарной площадки до координатной плоскости XOY, получим некоторый элементарный объем abcd, равный h· _xoy, т.е. объем, записанный под вторым интегралом в уравнении (2.36).Это уравнение теперь можно записать в виде

Р_В=р₀ + (объем ABCД). (2.38)

Следовательно, вертикальная составляющая силы абсолютного гидростатического давления равна сумме силы внешнего давления на горизонтальную проекцию цилиндрической поверхности АВ (пе­редающегося от воздействия внешней силы на поверхность жидкости) и веса жидкости в объеме АВСД, ограниченном цилиндрической по­верхностью АВ, вертикальными плоскостями АД и ВС свободной по­верхности жидкости, а также передней и задней вертикальными плоскостями.

Второй интеграл уравнения (2.37) равен статическому моменту площади проекции цилиндрической поверхности АВ на вертикальную плоскость ZOY относительно оси OY:

, (2.39)

где h_с − глубина погружения центра тяжести площади .

Из уравнений (2.37) и (2.39) находим

P_Г =(p₀+ _c)· . (2.40)

Это уравнение идентично уравнению (2.25). Следовательно, го­ризонтальная составляющая силы полного гидростатического давле­ния на цилиндрическую поверхность АВ равна силе абсолютного гидростатического давления, под воздействием которого находится вертикальная плоская стенка, равная по площади вертикальной про­екции цилиндрической поверхности АВ.

Складывая составляющие силы давления Р_В и Р_Г по правилу параллелограмма, получаем силу абсолютного гидростатического давления Р, действующую на цилиндрическую поверхность АВ:

. (2.41)

Построим эпюру абсолютного гидростатического давления на криволинейную поверхность АВ. Объем АВС₁Д₁ является эпюрой вертикальной составляющей абсолютного гидростатического давления на рассматриваемую поверхность АВ (рис. 10).

Рис.10

Эту эпюру можно рассматривать как состоящую из двух частей: эпюры АВСД, изобретающей избыточное (весовое) давление на площадь проекции поверхности АВ на плоскость XOY, и эпюры ДСС₁Д₁, характеризующей внешнее давление р₀. Сила давления Р_В, равная численно объему АВС₁Д₁, проходит через центр тяжести этого объема.

Эпюра горизонтальной составляющей абсолютного гидростатического давления на криволинейную поверхность АВ строится так же, как и для плоских стенок. В данном случае она представляется фигурой KZMN, которую можно рассматривать как состоящую из двух частей: эпюры KZM₁N₁, изображающей избыточное (весовое) давление жидкости, и эпюры MNN₁M₁, характеризующей внешнее давление р₀. Сила давления Р_T, равная объему эпюры KZM₁N₁, проходит через центр тяжести этого объема.