2.8. Действия над числовыми функциями
Определение. Функции, принимающие числовые значения, называются числовыми функциями.
Над функциями можно производить различные арифметические операции. Пусть заданы две числовые функции и , определенные на одном и том же множестве .
:
,
:
,
тогда
1)
:
определяется равенством
;
2)
:
определяется равенством
,
3)
:
определяется равенством
,
где
- некоторое число,
4)
:
определяется равенством
при условии, что
,
.
Пример.
Пусть
:
,
,
:
,
.
Определим функции
:
,
;
:
,
;
:
,
.
не определена, так
как
.
Упражнения для самостоятельной работы
Для функции : ,
найти
,
,
,
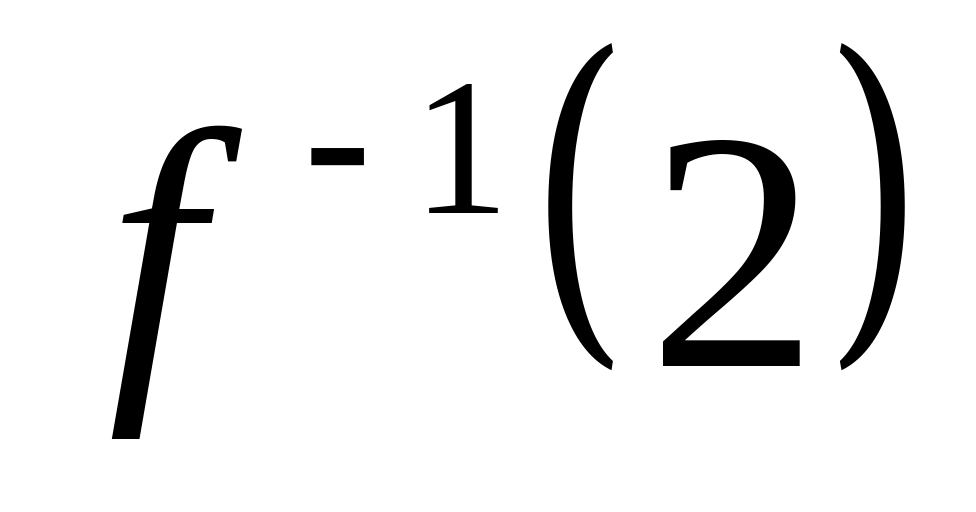.Для функции : ,
найти
,
,
,
,
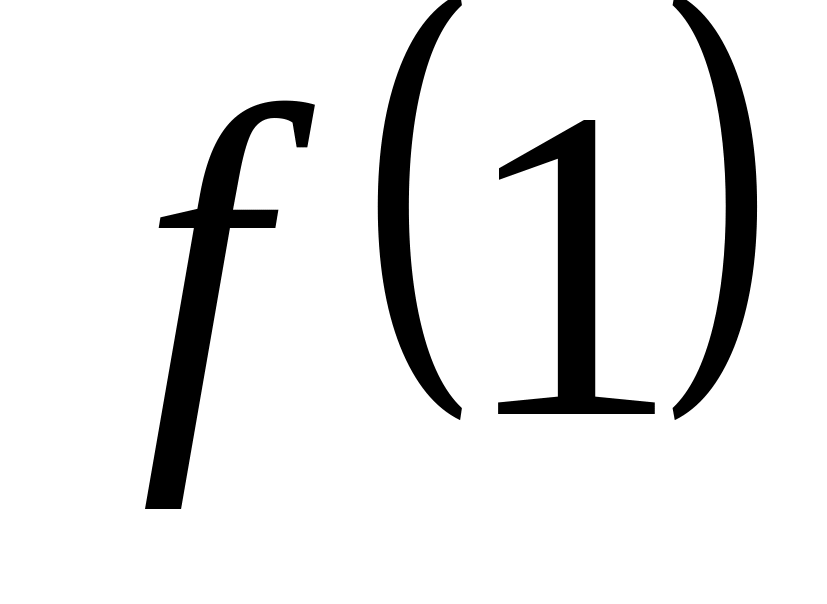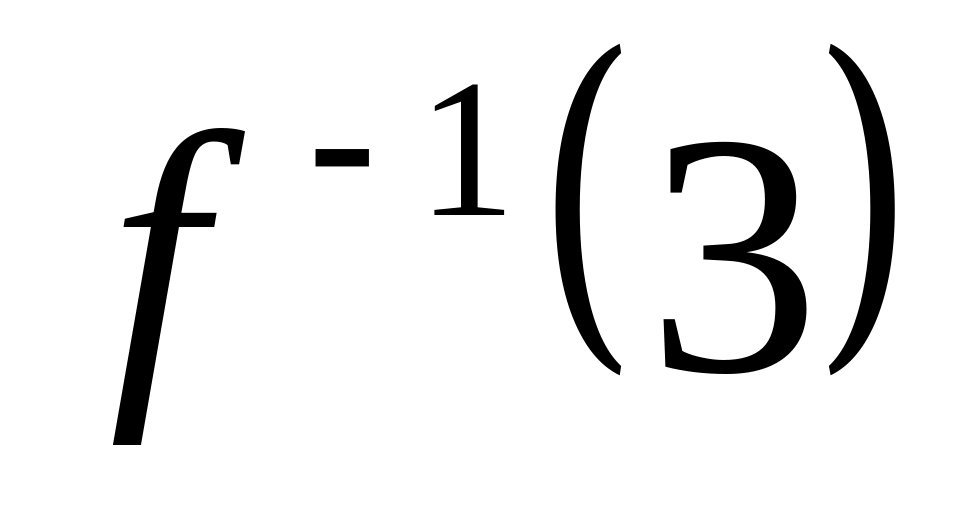построить график.Даны функции : ,
,
:
,
,
:
,
.
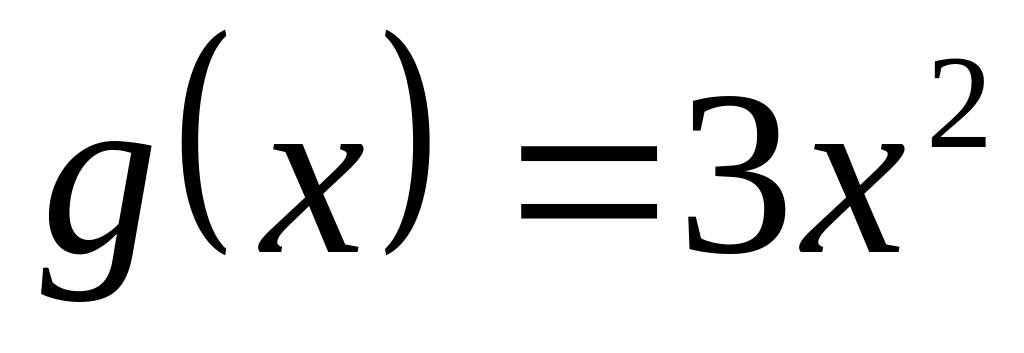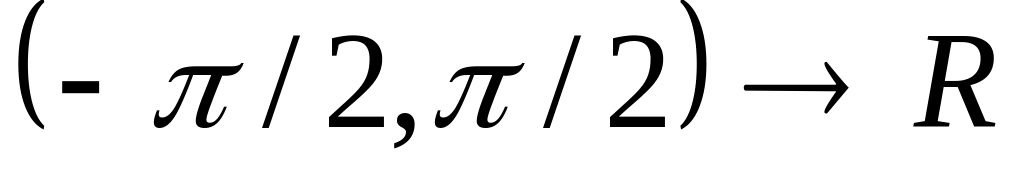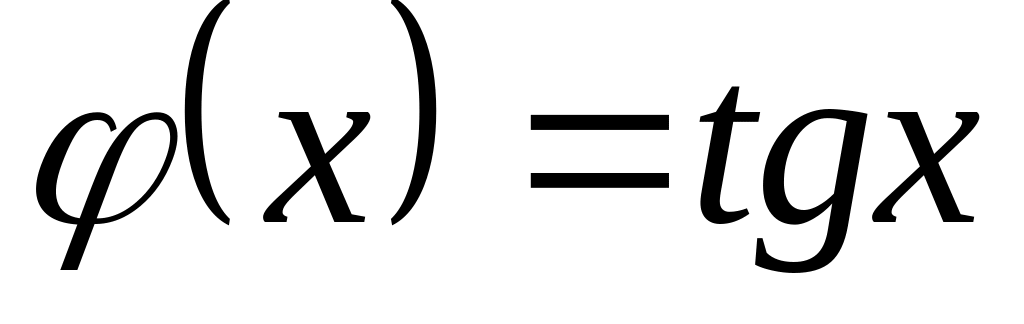Найти
,
,
,
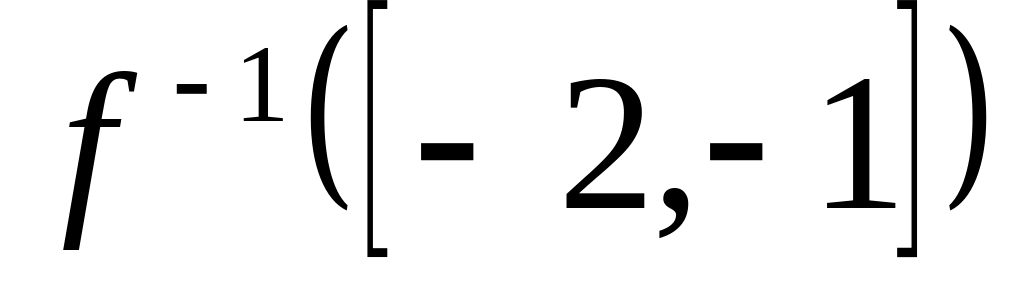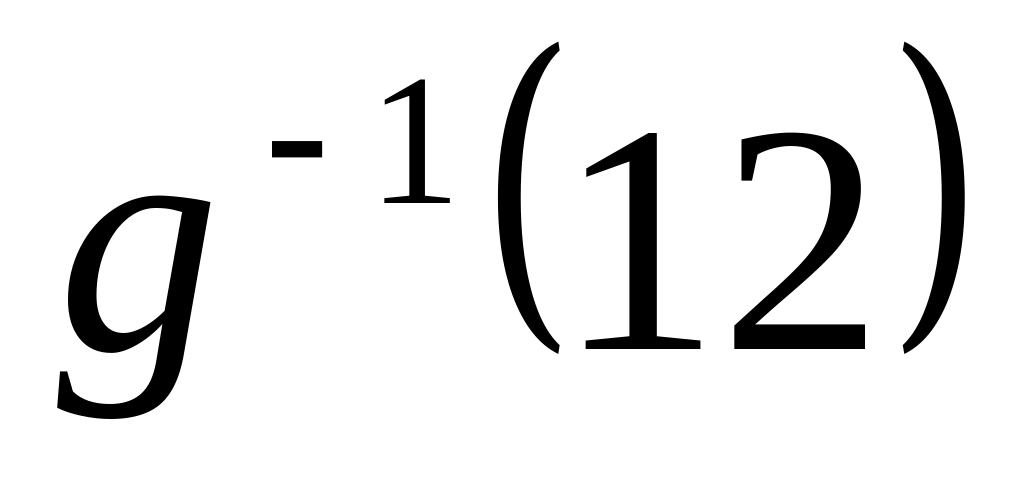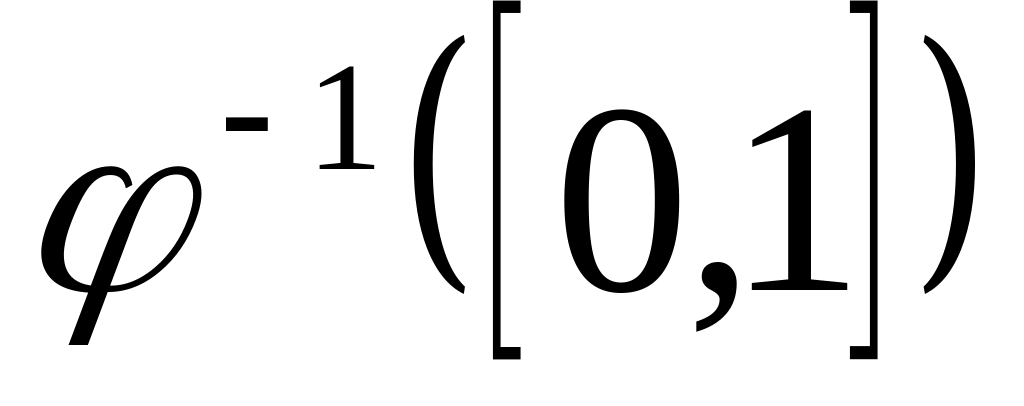построить график.Какие из данных отображений являются инъекцией, сюръекцией, биекцией:
а) : , ;
б) : , ;
в)
:
,
;
г)
:
,
;
д)
:
,
;
е) : , .
5. Пусть
:
и
,
.
Проверить справедливость следующих
соотношений:
,
и если
,
то
.
6. Пусть
:
и
,
.
Проверить справедливость следующих
соотношений:
,
,
если
,
то
,
.
7. Даны
:
,
;
:
,
.
Определить
,
.
8. Для функций
:
,
;
:
,
определить
,
.
9. Для функций
:
,
;
:
,
,
определить
,
.
10. Для функций : , и :
-
-1
0
1
2
3
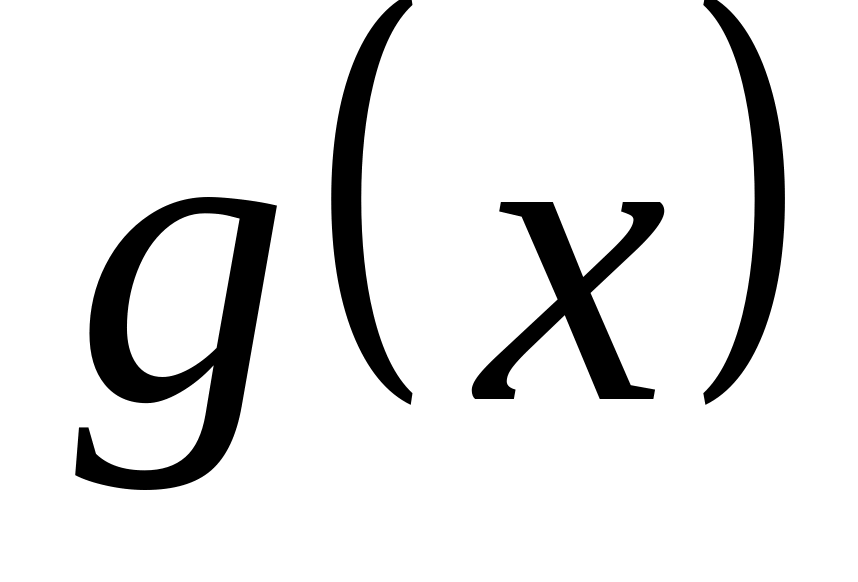
1
-1
1
3
4
определить , .
11. Проверить, какие из следующих отображений являются обратимыми. Для обратимых функций определить обратные:
а)
:
,
;
б)
,
;
в)
:
,
;
г)
:
,
;
д)
:
-
0
2
3
4
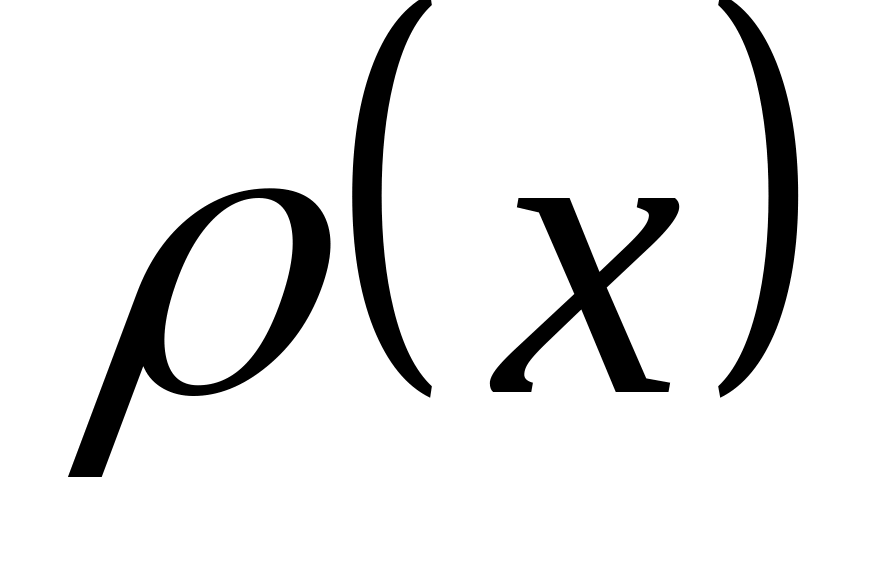
-1
3
1
-1
:
-
-1
0
3
5
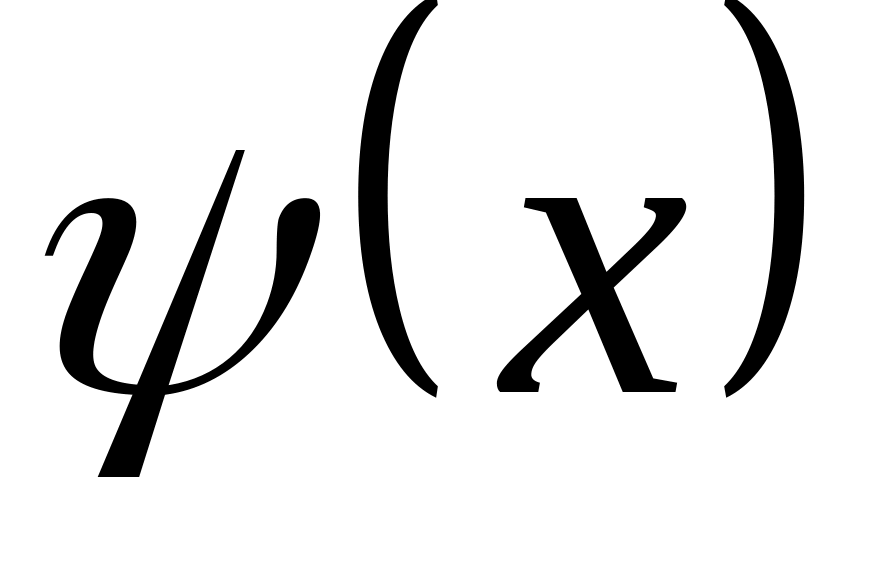
3
2
0
-1
12. Проверить
следующее утверждение: если
:
и
:
- два биективных отображения, то
отображение
также биективно и его обратным отображением
будет отображение
.
13. Для функций
:
,
;
:
,
определить
,
.
14. Заданы числовые
функции
:
,
;
:
,
.
Определить функции
,
,
,
.
15. Определить
,
,
,
,
если
:
,
;
:
,
.
Литература
1. Колмоговоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. – М.: Наука, 1976.
2. Канторович Л.В., Акилов Г.П. Функциональный анализ. – М.: Наука, 1977.
3. Ильин В.А., Садовничий В.А., Сендов Б.Х. Математический анализ. – М.: МГУ, 1985.
4. Кудрявцев Л.Д. Математический анализ. Т.1. – М.: Высшая школа, 1973.
5. Шнейдер В.Е., Слуцкий А.И., Шумов А.С. Краткий курс высшей математики. – М.: Высшая школа, 1978.