
- •Элементы теории множеств. Функции Методические указания
- •Содержание
- •Основные обозначения
- •1. Элементы теории множеств
- •1.1. Множества
- •Способы задания множеств
- •1.2. Операции над множествами
- •Декартово произведение множеств
- •Сечения упорядоченных множеств
- •Свойство 10 означает, что каждое действительное число принадлежит по крайней мере, одному из множеств и .
- •Упражнения для самостоятельной работы
- •2. Элементы теории функций
- •2.1. Отображения и функции
- •2.2. Способы задания функций
- •2.3. Образ и прообраз элемента, множества
- •2.4. Композиция отображений
- •2.5. Обратимые и обратные отображения
- •2.6. Инъективные, сюръективные отображения
- •2.7. Графики взаимнообратных функций
- •2.8. Действия над числовыми функциями
- •Определим функции
- •Упражнения для самостоятельной работы
- •Литература
- •Г.А.Батищева, н.Н.Киселева Элементы теории множеств. Функции Методические указания по изучению курса высшей математики
- •344007, Ростов-на-Дону, ул. Б.Садовая, 69. Ргэу. Издательство.
2.6. Инъективные, сюръективные отображения
Определение 1. Отображение : называется инъективным или инъекцией, если два различных элемента из множества имеют образами при отображении два различных элемента из множества , т.е.
![]() ,
,
![]()
![]() .
.
Например, отображение : приведенное на следующей схеме

![]()
является инъекцией
множества
в множество
.
Здесь
![]() .
.
Определение 2. Отображение : называется сюръективным или сюръекцией, если каждый элемент из множества является образом при отображении по крайней мере одного элемента из , т.е.
![]() такой, что
,
т.е.
такой, что
,
т.е.
![]() .
.
Сюръективное отображение – это отображение множества на множество .
Например, отображение :

является сюръективным, а отображение :

не является сюръективным.
Если
![]() при отображении
:
,
то отображение
- сюръективное.
при отображении
:
,
то отображение
- сюръективное.
Теорема. Отображение : биективно тогда и только тогда, когда оно инъективно и сюръективно одновременно.
Доказательство. Пусть : - биективно. Тогда каждый элемент является образом при отображении некоторого элемента , следовательно, отображение - сюръективно. А так как этот элемент - единственный, то из этого следует, что разным элементам соответствуют разные образы, т.е. отображение инъективно.
Обратно, пусть : - инъективно и сюръективно одновременно. Тогда в силу сюръекции , а ввиду инъективности отображения содержит единственный элемент.
Примеры.
1.
![]() ,
,
Отображение
не сюръективно, т.к. элемент
![]() не является образом ни одного элемента
из
не является образом ни одного элемента
из
![]() .
Оно не является и инъективным, т.к. два
различных элемента
.
Оно не является и инъективным, т.к. два
различных элемента
![]() и
и
![]() имеют образом один и тот же элемент
имеют образом один и тот же элемент
![]() .
.
2.
:
![]() ,
,
Отображение сюръективно, но не инъективно.
3.
![]() :
:
![]() ,
,
![]()
Отображение сюръективно и инъективно одновременно, т.к. оно биективно.
2.7. Графики взаимнообратных функций
1.
:
,
,
![]() - нечетное.
- нечетное.
Уравнение
![]() для любого
для любого
![]() имеет единственное решение
имеет единственное решение
![]() ,
поэтому функция
:
обратима и имеет обратную функцию
:
по правилу
.
,
поэтому функция
:
обратима и имеет обратную функцию
:
по правилу
.
Обозначим аргумент обратной функции через , получим
:
,
![]() .
.
Рассмотрим графики функций и .
![]()
![]() .
.
График обратной функции (рис. 6б) симметричен графику функции (рис. 6а) относительно биссектрисы первого и третьего координатных углов.

0 0
Рис. 6а Рис. 6б
2. Отметим, что следующая функция не обратима:
: , , - четное.
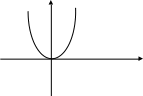
0
Рис. 7
3.
:
![]() ,
,
![]() ,
,
![]()
:
,
![]() .
.

![]()
![]()
![]()
![]()
0 0
Рис. 8а Рис. 8б
4.
:
![]() ,
,
![]() ,
,
![]() - нечетное
- нечетное
:
,
![]() .
.

![]()
0 0
Рис. 9а Рис. 9б
5.
:
![]() ,
,
,
,
![]() - четное. Эта
функция не обратима.
- четное. Эта
функция не обратима.

0
Рис. 10
6.
:
,
![]() ,
,
:
,
![]() .
.

1 1
![]()
0 1 0 1
Рис. 11а Рис. 11б
7.
:
![]() ,
,
![]() ,
,
,
,
![]() ,
,
:
![]() ,
,
![]() .
.


1
![]()
0 0 1
Рис. 12а
Рис. 12б
8.
:
![]() ,
,
![]() ,
,
:
![]() ,
,
![]() .
.

![]()





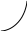 1
1
![]()






![]() 0 1
-1
0 1
0 1
-1
0 1
 -1
-1
![]()

Рис. 13а Рис. 13б
9.
:
![]() ,
,
![]() ,
,
:
![]() ,
,
![]() .
.
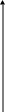
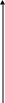



![]()

 1
1
![]()
![]()


 0
0
![]() -1 0 1
-1 0 1
 -1
-1
Рис. 14а Рис. 14б
10.
:
![]() ,
,
![]() ,
,
:
![]() ,
,
![]() .
.
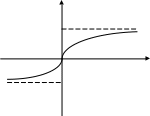
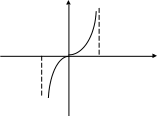
0 0
Рис. 15а Рис. 15б
11.
:
![]() ,
,
![]() ,
,
:
![]() ,
,
![]() .
.
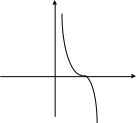
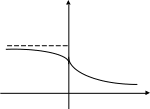
![]()
 0
0
0
Рис. 16а Рис. 16б
