2.2. Способы задания функций
Аналитический способ задания функции
Если функция выражена при помощи формулы (аналитического выражения), позволяющего для значения вычислить (определить) значение функции (образ элемента ) , то говорят, что она задана аналитически.
Пример.
Рассмотрим функцию
,
определенную формулой
и являющуюся отображением множества
действительных чисел
во множеством неотрицательных чисел
,
т.е.
,
.
Заметим, что вполне
возможно рассматривать отображение
в
,
определенное соотношением
,
т.е.
,
;
Функции и различны, хотя и заданы одним и тем же аналитическим выражением, т.к. имеют различные области определения.
Табличный способ задания функции
Если - конечное множество, то функция может быть задана таблично:
|
|
|
|
|
|
|
|
В верхней строке перечисляются элементы множества определения функции , в нижней указываются их образы. Например,
-
1
2
3
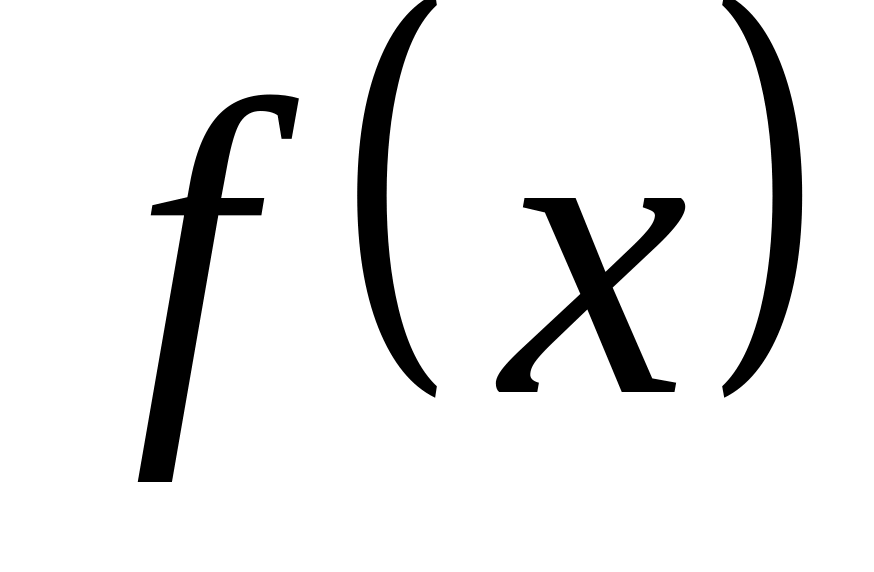
0
-1
5
От аналитического способы задания функции всегда можно перейти к табличному, а обратный переход в общем случае сделать нельзя.
Задание графиком.
При графическом способе задания функции соответствие между переменными устанавливается с помощью графика.
Определение 1.
Графиком
функции
:
называется подмножество
в декартовом произведении
вида:
.
Нетрудно видеть, что функция однозначно определяет график и наоборот, по графику функция восстанавливается однозначно.
Примеры.
1. Функция
:
,
задается графиком
,
.
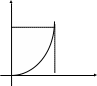
2
1
0 1
Рис. 3
2. Рассмотрим
функцию
,
,
где
- множество целых чисел,
- целая часть, наибольшее целое число,
не превосходящее
.
На каждом промежутке
,
где
функция
постоянна и
.
График данной функции изображен на рис. 4. Стрелки на графике означают, что точки на острие стрелки графику не принадлежат.
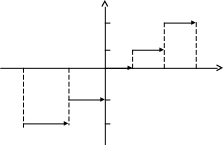
2
1
–2 –1 0 1 2 3
-1
-2
Рис. 4
4.Функция, заданная таблицей
-
1
2
3
2
1
0
Может быть задана графиком (рис.5)
2
1
0 1 2 3
Рис. 5
2.3. Образ и прообраз элемента, множества
Пусть задано
отображение
:
и пусть множество
является подмножеством множества
,
т.е.
.
Обозначим через
подмножество множества
,
образованное из всех элементов
,
где
,
т.е.
.
Определение 1. Подмножество называется образом подмножества при отображении .
Определение 2.
Совокупность всех тех элементов
,
образом которых является данный элемент
,
,
называется прообразом
элемента
при отображении
и обозначается
.
Очевидно, если
,
то
.
Например, пусть
,
где
,
тогда
.
Определение 3.
Пусть множество
.
Прообразом
множества
при отображении
называется множество элементов
,
таких, что
и обозначается
:
.
Очевидно, что
.
Примеры.
1.
2.
,
,
,
3. Функция задана с помощью таблицы:
-
-1
2
4
5
1
0
1
2
,
,
,
.