1.4. Структурная и приведенная формы эконометрических моделей

Для построения прогнозов эндогенных переменных необходимо выразить текущие эндогенные переменные модели в виде явных функций предопределённых переменных. Спецификация (1.17) получена в результате математической формализации экономических закономерностей. Такая форма спецификации называется структурной. В общем случае в структурной спецификации эндогенные переменные не выражены в явном виде через предопределенные. В модели равновесного рынка (1.17) только переменная предложения Y’ выражена в явном виде через предопределенную переменную, поэтому для представления эндогенных переменных через предопределенные необходимо выполнить некоторые преобразования структурной формы. Решим систему уравнений (1.17)

Y_t^d = а₀ + а₁∙р_t + а₂∙х_{t +} v_t, а₁ <0, а₂ >0,

Y_t^s =b₀ + b₁∙р_{t-1 +} w_t, b₁ > 0,

Y^d=Y^s.

относительно эндогенных переменных. Подставим первое и второе уравнения в третье:

а₀ + а₁∙р_t + а₂∙х_{t +} v_t = b₀ + b₁∙р_{t-1 +} w_t,

и выразим текущее значение цены равновесия через предопределенные переменные:

(1.19)

где с₁ < 0, с₂ > 0,

Подставляя первую часть из уравнения (1.19) в Y^d системы (1.17), получим выражение спроса через предопределенные переменные:

Таким образом, после преобразований спецификация модели (1.17) принимает следующий вид:

Y_t^d = b₀ + b₁∙р_t-1 + ε_t,

Y_t^s = b₀ + b₁∙р_t-1 + ε_t, (1.20)

,

b₁ > 0, с₁ <0, с₂ >0.

Эндогенные переменные модели (1.20) выражены в явном виде через предопределенные переменные. Такая форма спецификации получила название приведенной. В частном случае структурная и приведённая формы модели могут совпадать. При правильной спецификации модели переход от структурной к приведённой форме всегда возможен, обратный переход - нет.

См. дополнительно литературу: [1, с. 69-71]; [2, с. 66 - 117]; [8]; [9].

1.5. Матричная запись структурной и приведенной форм моделей

Представим структурную форму модели в матричном виде. Введем следующие обозначения:

Y_t — вектор-столбец текущих значений эндогенных переменных;

X_t — расширенный вектор-столбец предопределённых переменных, значения которых известны к моменту t;

А и В — матрицы коэффициентов структурной формы модели (структурные коэффициенты);

V_t — вектор-столбец текущих возмущений.

С учетом данных обозначений матричная запись структурной формы эконометрической модели принимает вид

A∙Y_t+B∙X_t=V_t. (1.21)

Представим спецификацию (1.17) модели равновесного рынка в форме (1.20). Для этого предварительно в каждом уравнении системы перенесем все члены (кроме случайных возмущений) в левую часть:

Y_t^d - а₀ - а₁∙р_t - а₂∙х_t = v_t, а₁ <0, а₂ >0,

Y_t^s - b₀ - b₁∙р_t-1 = w_t, b₁ > 0, (1.22)

Y^d- Y^s = 0.

Модель равновесного рынка предназначена для оценки (или про­гнозирования) текущих значений спроса, предложения и равновесной цены, поэтому элементы вектора эндогенных переменных следующие:

Предопределенные переменные модели — лаговое значение цены товара и текущий доход потребителя, следовательно, расширенный вектор X, включает три элемента: Единичный элемент данного расширенного вектора позволяет учесть наличие свободного члена в поведенческих уравнениях, входящих в систему.

Элементами вектора V_t в модели (1.22) являются текущие возмущения соответствующих поведенческих уравнений и нулевой элемент — правая часть уравнения тождества

Матрицы структурных коэффициентов А и В состоят из следующих элементов:

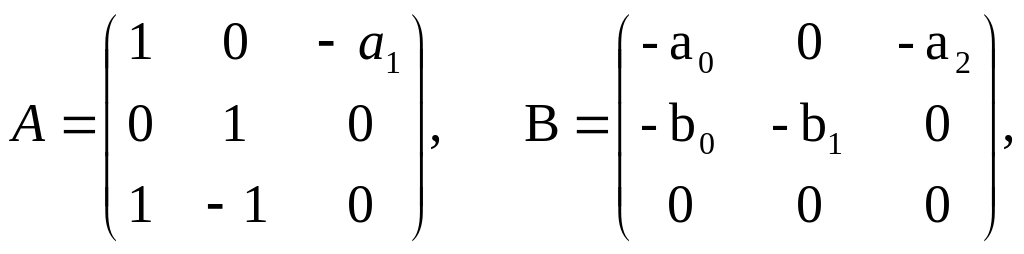(1.23)

В соответствии со вторым принципом спецификации, число уравнений системы равно числу эндогенных переменных модели. Поэтому матрица А структурных коэффициент – квадратичная. Матрица В может быть прямоугольной. Число строк матрицы В должно совпадать с числом строк матрицы А.

Определитель матрицы А равен: det A= –a₁

Матричное представление приведённой формы спецификации следующее:

(1.24)

где М – матрица приведенных коэффициентов, которая рассчитывается как

М = -А^-1∙В, (1.25)

Матрицу М можно получить в результате решения матричного уравнения (1.20). Для этого правую и левую часть данного уравнения умножим на обратную матрицу А^-1 (следовательно, для построения приведенной формы необходимо и достаточно, чтобы матрица А структурных коэффициентов была обратима).

Для спецификации (1.22) имеем:

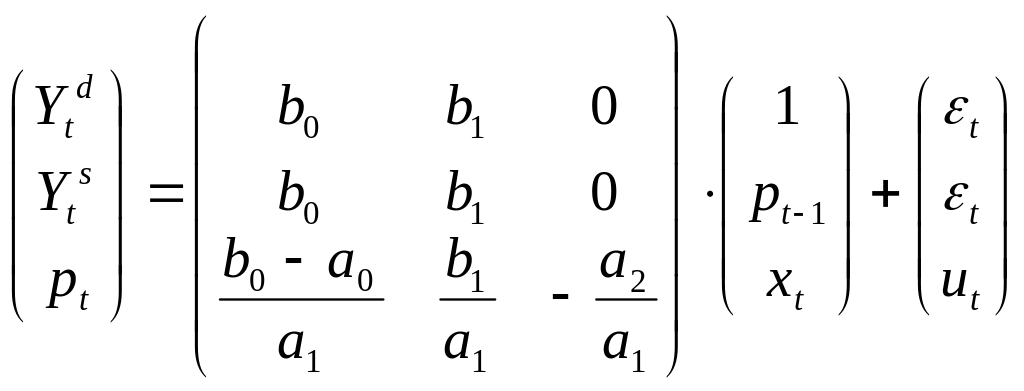(1.26)

Вектор случайных возмущений в приведённой форме получается в результате преобразования

(1.27)

и, соответственно, определяется как

(1.28)

См. дополнительно литературу: [1, с. 69-71]; [2, с. 66 - 117]; [8]; [9].