2. Подбор объясняющих переменных для множественной линейной модели

Имеется множественная линейная эконометрическая модель, спецификация которой представлена в виде:

y_t= a₁∙x_t1 + a₂∙x_t2 + a₃∙x_t3 + … + a_m∙x_tm + u_t , (2.1)

t = 1, …, n,

где

m – число параметров модели;

n – объем выборки;

y_t – объясняемая переменная в наблюдении t;

x_tm – объясняющие переменные в наблюдении t;

u_t – случайное возмущение в наблюдении t;

Матричная форма спецификации модели имеет вид:

Y = A∙X + U, (2.2)

где

Y = (y₁, y₂, y₃, …, y_n)^T – вектор-столбец значений объясняемой (эндогенной) переменной;

- детерминированная матрица объясняющих переменных;

A = (a₁, a₂, a₃, …, a_m)^T - вектор столбец параметров модели;

U = (u₁, u₂, u₃, …, u_m)^T – вектор-столбец случайных возмущений.

С формальной точки зрения, объясняющие переменные в линейной эконометрической модели должны обладать следующими свойствами:

• иметь высокую вариабельность;

• быть сильно коррелированными с объясняемой переменной;

• быть слабо коррелированными между собой;

• быть сильно коррелированными с представляемыми ими другими переменными, не используемыми в качестве объясняющих.

Объясняющие переменные подбираются с помощью статистических методов. Процедура подбора переменных состоит из следующих этапов:

1. На основе накопленных знаний составляется множество так называемых потенциальных объясняющих переменных (первичных переменных), в которое включаются все важнейшие величины, влияющие на объясняемую переменную, т.е. переменные x₁, x₂, ..., x_т.

2. Собирается статистическая информация о реализациях, как объясняемой переменной, так и потенциальных объясняющих переменных.

3. Формируется вектор Y наблюдаемых значений переменной y и матрица X наблюдаемых значений переменных x₁, x₂, ..., x_т в виде, как представлено в пояснении к формуле 2.2.

4. Исключаются потенциальные объясняющие переменные, характеризующиеся слишком низким уровнем вариабельности.

5. Рассчитываются коэффициенты корреляции между всеми рассматриваемыми переменными.

6. Множество потенциальных объясняющих переменных редуцируется с помощью выбранной статистической процедуры.

Метод «Исключение квазинеизменных переменных»

Предварительным условием присвоения различным величинам статуса объясняющих переменных считается достаточно высокая их вариабельность. В качестве меры вариабельности используется коэффициент вариации

(2.3)

где

— среднее арифметическое переменной X_i, рассчитываемое по формуле:

(2.4)

т огда как S_i — стандартное отклонение переменной X_i, рассчитываемое по формуле:

(2.5)

Задается критическое значение коэффициента вариации v*³, и тогда, переменные, удовлетворяющие неравенству

v_i <v* (2.6)

признаются квазинеизменными и исключаются из множества потенциальных объясняющих переменных, так как не несут значимой информации.

Метод анализа вектора и матрицы коэффициентов корреляции

Идея данного метода сводится к выбору таких объясняющих переменных, которые сильно коррелируют с объясняемой переменной и, одновременно, слабо коррелируют между собой. В качестве исходных данных рассматриваются значения коэффициентов корреляции вектора R₀, рассчитанные по формуле (1.14), и значения коэффициентов корреляции матрицы R, рассчитанные по формуле (1.16).

В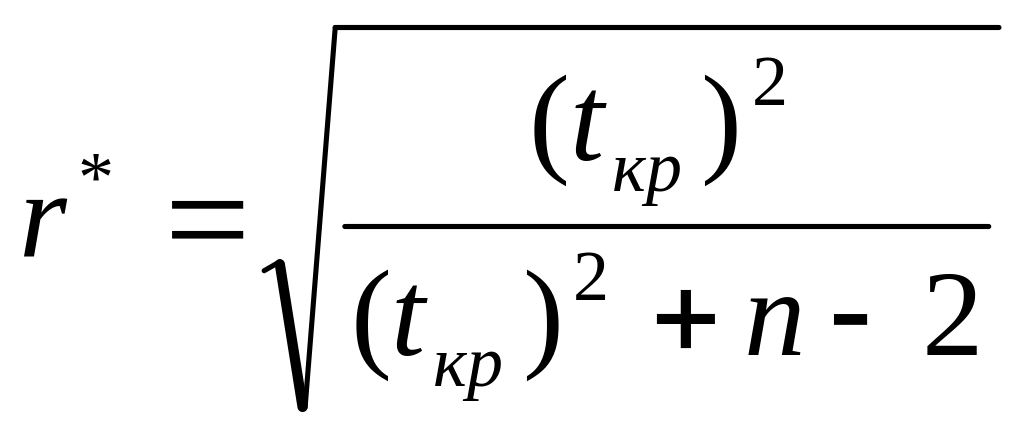 начале рассчитывается, так называемое, критическое значение коэффициента корреляции r* по формуле:

(2.7)

где t_кр — значение t-распределения Стьюдента для заданного α (берется 0,05) и для (п - 2) степеней свободы.

Критическое значение коэффициента корреляции r* также может априорно задаваться аналитиком.

Алгоритм подбора объясняющих переменных следующий:

1. Из множества потенциальных объясняющих переменных сначала исключаются все элементы, у которых коэффициенты корреляции в векторе R₀ удовлетворяют неравенству abs(r_i) < r*. Такие объясняющие переменные несущественно коррелируют с объясняемой переменной.

2. Из оставшихся переменных объясняющей признается такая переменная Х_h, для которой |r_h| = max{r_i}, поскольку Х_h является носителем наибольшего количества информации об объясняемой переменной.

3. Из множества потенциальных объясняющих переменных исключаются все элементы, у которых коэффициенты корреляции в строке h матрицы корреляции удовлетворяют неравенству r_hi > r*, поскольку эти переменные слишком сильно коррелируют с объясняющей переменной, и, следовательно, только воспроизводят представляемую ею информацию.

Пункты 1 - 3 повторяются вплоть до момента опустошения множества потенциальных объясняющих переменных.

Метод показателей информационной емкости

Данный метод сводится к выбору таких объясняющих переменных, которые сильно коррелированы с объясняемой переменной, и одновременно, слабо коррелированы между собой. В качестве исходных значений в данном методе рассматриваются вектор R₀ и матрица R.

Рассматриваются все комбинации потенциальных объясняющих переменных, общее количество которых составляет

L = 2^т-1 (2.8)

где m – число потенциальных объясняющих переменных

Для каждой комбинации потенциальных объясняющих переменных рассчитываются индивидуальные и интегральные показатели информационной емкости.

Индивидуальные показатели информационной емкости в рамках конкретной комбинации рассчитываются по формуле

(2.9)

где l - номер переменной,

m_l — количество переменных в рассматриваемой комбинации.

Интегральные показатели информационной емкости потенциальных объясняющих переменных рассчитываются по формуле

(2.10)

Индивидуальные и интегральные показатели информационной емкости нормируются в интервале [0; 1]. Их значения оказываются тем больше, чем сильнее объясняющие переменные коррелируют с объясняемой переменной и чем слабее они коррелируют между собой.

В качестве объясняющих выбирается такая комбинация переменных, которой соответствует максимальное значение интегрального показателя информационной емкости, т.е

. (2.11)

См. дополнительно литературу:[9, с. 15 - 33]; [10]; [11].