
- •«Разностные уравнения и их приложения – 14 вопросов»
- •«Дифференциальные уравнения и их приложения в биологии »
- •Барометрическая формула
- •Гармонические колебания
- •29. Задание {{ 29 }} тз 29 Тема 1-3-0
- •30. Задание {{ 33 }} тз 33 Тема 1-2-0
- •Механические волны
- •49. Задание {{ 57 }} тз 42 Тема 1-4-0
- •50. Задание {{ 58 }} тз 43-Тема 1-3-0
- •51. Задание {{ 59 }} тз 44 Тема 1-3-0
- •Раздел 2.Термодинамика эффект доплера
- •Идеальный газ
- •72. Задание {{ 93 }} тз 71 Тема 1-5-0
- •83. Задание {{ 175 }} тз 140 Тема 1-5-0
- •84. Задание {{ 176 }} тз 141 Тема 1-5-0
- •85. Задание {{ 177 }} тз 142 Тема 1-5-0
- •86. Задание {{ 178 }} тз 143 Тема 1-5-0
- •96. Задание {{ 188 }} тз 151 Тема 1-5-0
- •Раздел 3. Модели кравообращения
- •97. Задание {{ 98 }} тз 76 Тема 1-5-0
- •98. Задание {{ 99 }} тз 77 Тема 1-5-0
- •Раздел 4. Механика
- •Раздел 5. Электричество
- •Раздел 6. Молекулярная физика
- •Раздел 7. Задачи
- •240. Задание {{ 287 }} тз 250 Тема 1-6-0
- •241. Задание {{ 288 }} тз 251 Тема 1-6-0
- •242. Задание {{ 289 }} тз 252 Тема 1-6-0
- •V1: гармонические колебания
- •V1: механические волны
- •V1: статобработка
- •V1: эффект доплера
- •V1: электрическое поле
- •V1: контактные явления
- •V1: магнитное поле
- •V1: направление вектора магнитной индукции
- •V1: электромагнитная индукция
- •V1: электромагнитные колебания
- •V1: переменный ток
- •V1: дифракция света
- •V1: интерференция света
- •V1: поляризация света
- •V1: природа света
- •V1: строение атома
«Разностные уравнения и их приложения – 14 вопросов»
Порядок разностного уравнения
 равен …5;
равен …5;Порядок разностного уравнения
 равен …3;
равен …3;Характеристическое уравнение соответствующее разностному уравнению
 имеет корни +: 2, 3;
имеет корни +: 2, 3;Характеристическое уравнение соответствующее разностному уравнению
 имеет корни 1, 7;
имеет корни 1, 7;Характеристическое уравнение соответствующее разностному уравнению
 имеет вид
имеет вид

Характеристическое уравнение соответствующее разностному уравнению
 имеет вид
имеет вид

Общее решение разностного уравнения
 имеет вид
имеет вид

Общее решение разностного уравнения имеет вид

Разностное уравнение
 является линейным и неоднородным
является линейным и неоднороднымРазностное уравнение
 является линейным и однородным
является линейным и однороднымРазностное уравнение
 является нелинейным и однородным
является нелинейным и однороднымРазностное уравнение
 является нелинейным и неоднородным
является нелинейным и неоднороднымРешение разностного уравнения
 с начальным условием
с начальным условием
 имеет
вид
имеет
вид

Решение разностного уравнения
 с начальным условием
имеет
вид
с начальным условием
имеет
вид

«Дифференциальные уравнения и их приложения в биологии »
Дифференциальное уравнение
 является
линейным и неоднородным
является
линейным и неоднороднымДифференциальное уравнение
 является
линейным и однородным
является
линейным и однороднымДифференциальное уравнение
 является
нелинейным и однородным
является
нелинейным и однороднымДифференциальное уравнение
 является
нелинейным и неоднородным
является
нелинейным и неоднороднымS: Общее решение дифференциального уравнения
 имеет вид
имеет вид

Общее решение дифференциального уравнения
 имеет вид
имеет вид

Порядок дифференциального уравнения
 равен 3
равен 3S: Порядок дифференциального уравнения
 равен 2
равен 2S: Решение дифференциального уравнения
 с
начальным условием
имеет вид
с
начальным условием
имеет вид

Решение дифференциального уравнения
 с
начальным условием
имеет вид
с
начальным условием
имеет вид

«Классическое определение вероятности»
Игральный кубик бросают один раз. Событие А – «Выпало число очков большее, чем 3». Событие В – «Выпало число очков меньшее, чем 3». Тогда для этих событий верным будет утверждение: «События А и В несовместны»
В урне 10 белых шаров. Опыт состоит в выборе только одного шара. Событие А – «Вынули белый шар». Событие В – «Вынули черный шар». Тогда для этих событий верным будет утверждение: «Событие А достоверно»
В ящике 5 качественных и 5 бракованных изделий. Опыт состоит в выборе только одного изделия. Событие А – «Вынули качественное изделие». Событие В – «Вынули бракованное изделие». Тогда для этих событий верным будет утверждение: «События А и В равновероятны»
Вероятность наступления некоторого события не может быть равна ... 1,3
Из урны, в которой находятся 4 белых и 8 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна…
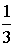
Из урны, в которой находятся 4 белых и 7 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна…
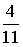
S: Из урны, в которой находятся 4 белых и 9 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна…
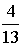
S: Из урны, в которой находятся 5 белых и 8 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна…
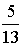
«Теоремы сложения и умножения вероятностей. Формула полной вероятности »
S: Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,5 и 0,4 соответственно. Тогда вероятность того, что в цель попадут оба стрелка, равна… 0,2
Футбольная команда выиграет первый матч с вероятностью 0,9, а второй – с вероятностью 0,4. Тогда вероятность того, что команда выиграет оба матча, равна 0,36
S: Студент Иванов придет на лекцию с вероятностью 0,2, а студент Петров – с вероятностью 0,8. Тогда вероятность того, что оба студента будут на лекции, равна …
0,16
Белый шар из первой урны можно вытащить с вероятностью 0,2; из второй – с вероятностью 0,7. Вытащили по одному шару из каждой урны. Тогда вероятность вытащить два белых шара равна … 0,14
Два одноклассника поступают в институт на разные факультеты. Первый одноклассник поступит с вероятностью 0,5; второй – с вероятностью 0,6. Тогда вероятность того, что оба одноклассника поступят, равна …0,3
В первой урне 4 белых и 6 черных шаров. Во второй урне 1 белый и 9 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна… 0,25
В первой урне 2 черных и 8 белых шаров. Во второй урне 3 белых и 7 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна… 0,55
В первой урне 1 черный и 9 белых шаров. Во второй урне 4 белых и 6 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна… 0,65
В первой урне 5 белых и 5 черных шаров. Во второй урне 3 черных и 7 белых шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна… 0,6
В первой урне 2 белых и 8 черных шаров. Во второй урне 3 белых и 7 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна… 0,25
«Числовые характеристики дискретных случайных величин»
Пусть X – дискретная случайная величина, заданная законом распределения вероятностей:
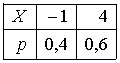 Тогда
математическое ожидание этой случайной
величины равно…2
Тогда
математическое ожидание этой случайной
величины равно…2
Пусть X – дискретная случайная величина, заданная законом распределения вероятностей:
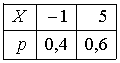 Тогда
математическое ожидание этой случайной
величины равно…2,6
Тогда
математическое ожидание этой случайной
величины равно…2,6
Пусть X – дискретная случайная величина, заданная законом распределения вероятностей:
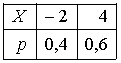 Тогда
математическое ожидание этой случайной
величины равно…1,6
Тогда
математическое ожидание этой случайной
величины равно…1,6
Пусть X – дискретная случайная величина, заданная законом распределения вероятностей:
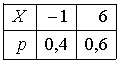 Тогда
математическое ожидание этой случайной
величины равно…3,2
Тогда
математическое ожидание этой случайной
величины равно…3,2
Пусть X – дискретная случайная величина, заданная законом распределения вероятностей:
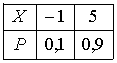 Тогда
математическое ожидание этой случайной
величины равно…4,4
Тогда
математическое ожидание этой случайной
величины равно…4,4
Дан закон распределения вероятностей дискретной случайной величины
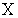 :
:
 Тогда
значение a равно… 0,3
Тогда
значение a равно… 0,3
Дан закон распределения вероятностей дискретной случайной величины :
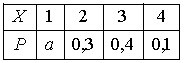 Тогда
значение a равно… 0,2
Тогда
значение a равно… 0,2
Дан закон распределения вероятностей дискретной случайной величины :
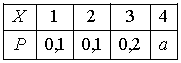 Тогда
значение a равно… 0,6
Тогда
значение a равно… 0,6
Дан закон распределения вероятностей дискретной случайной величины :
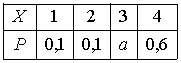 Тогда
значение a равно… 0,2
Тогда
значение a равно… 0,2
Дан закон распределения вероятностей дискретной случайной величины :
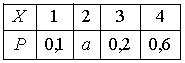 Тогда
значение a равно… 0,1
Тогда
значение a равно… 0,1
«Законы распределения вероятностей непрерывных случайных величин -10 вопросов»
График плотности распределения вероятностей непрерывной случайной величины Х имеет вид:
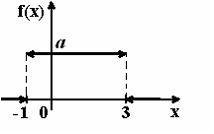 Тогда
значение а равно… 0,25
Тогда
значение а равно… 0,25
График плотности распределения вероятностей непрерывной случайной величины Х имеет вид:
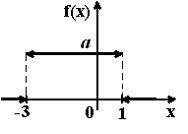 Тогда
значение а равно… 0,25
Тогда
значение а равно… 0,25
График плотности распределения вероятностей непрерывной случайной величины Х имеет вид:
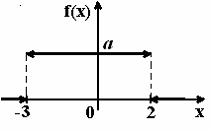 Тогда
значение а равно… 0,2
Тогда
значение а равно… 0,2
График плотности распределения вероятностей непрерывной случайной величины X имеет вид:
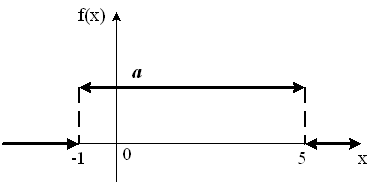 Тогда
значение a равно…
Тогда
значение a равно…
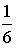
График плотности распределения вероятностей непрерывной случайной величины X имеет вид:
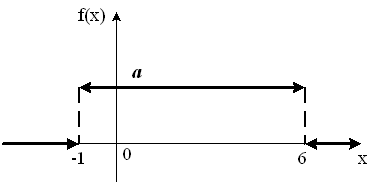 Тогда
значение a равно…
Тогда
значение a равно…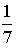
График плотности распределения вероятностей непрерывной случайной величины X имеет вид:
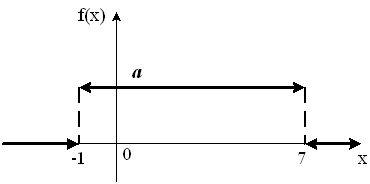 Тогда
значение a равно…
Тогда
значение a равно…
График плотности распределения вероятностей непрерывной случайной величины X имеет вид:
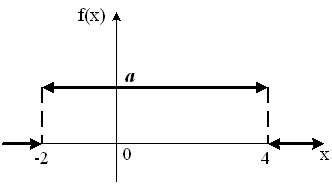 Тогда
значение a равно…
Тогда
значение a равно…
График плотности распределения вероятностей непрерывной случайной величины X имеет вид:
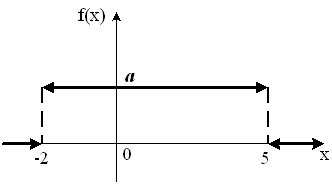 Тогда
значение a равно…
Тогда
значение a равно…
График плотности распределения вероятностей непрерывной случайной величины X имеет вид:
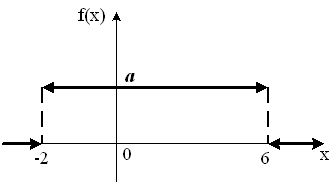 Тогда
значение a равно…
Тогда
значение a равно…
График плотности вероятностей для нормального распределения изображен на рисунке ...
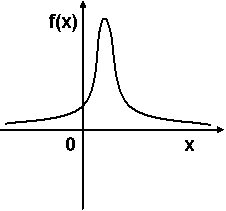
ФИЗИКА
Амплитудой колебаний называется: величина,численно равная наибольшему отклонению движущегося тела от положения равновесия
Атмосферное давление измеряется: барометром
Атомы в рамках Резерфордовского представления представляют собой: положительный заряд сосредоточен в центре, а электроны вращаются вокруг
В формуле T=2П корень l/g описывается колебание: математического маятника.
В формуле T=2П корень m/k описывается колебание: пружинного маятника.
В формуле гармонических колебаний А представляет: амплитуду
В формуле гармонических колебаний Х: смещение.
В явлении интерференции обнаруживаются свойства: волновые
Величина “Фи”0 : начальная фаза
Величина напряженности магнитного поля определяется как: отношение силы, с которой поле действует на единичный … тока, располагающийся перпендикулярно нулю.
Влажность воздуха определяется: гигрометром и психрометром
Восприимчивость вещества к намагничиванию под действием внешнего магнитного поля,называется: магнитной проницаемостью
Вязкость жидкости определяется: искозиметром
Гальванометр: регулируется на весьма малые силы тока
Гармонические колебания описываются уравнением: x=Acos(wt+ф)
Гармоническими называются колебания: при которой колеблюющаяся величина изменяются в зависимости от времени по закону синуса или косинуса
Дифракцией света называется: отклонение света от прямолинейного распределения в среде с разными неоднородн.
Дифракционная решетка используется для: получения дифракционных спектров
Дифракция света это: отклонение света от прямолинейности распространения в среде с резкими неравномерностями
Для измерения плотности потоков ионизирующих излучений используется: радиометр
Для магнитного поля непрерываемого прямолинейным проводником с током справедлива формула Ампера: dF=мю0I0dl0dH
Для определения величины напряженности магнитного поля в проводниках с током следует использовать выражение: dH=Idlsin”альфа”/ 4”пи”r2
Для определения концентрации веществ в контрастных ( окрашенных ) растворах используется: калориметр
Единицей измерения потенциала является: В
Единицей измерения силы электрического поля является: А
Единицей измерения сопротивления электрического поля является: Ом
Единицой измерения напряженности электрического поля является: В|м
Закон Ома для участка цепи: I=U|R
Измерение давления газов или жидкостей проводится: монометром
Индукция магнитного поля измеряется в: Тл
Интерференцией света называется явление : получение световых пучков от когерентных нейтронов.
Когерентными называются волны которые излучаются: из одного источника
Когерентными называются источники, которые излучают: с постоянной разностью фаз.
Математическим выражением третьего постулата Бора это: H “нью”= dB1/dB2 , здесь H “нью” ватт энергии, а dB1/dB2 энергия соответственно начальная и конечная
Модель атома Резерфорда была усовершенствована: Бором
Направление силы Ампера определяется: по закону левой руки
Напряженность магнитного поля измеряется в: А|м
Напряженность поля является его: силовой характеристикой
Напряженность электрического поля измеряется в : вольт/метр
Напряженность электрического поля определяется выражением: E=F|q
Недостатки Резерфордовской модели атома: в резерфордовской модели атом является неустойчивым образованием
Неподвижные электрические заряды взаимодействуют по закону: Кулона
Определение концентрации сахара в растворах производится: паляриметром
Освещенность измеряют: люксметром
Периодом колебаний называется: величина,численно равная времени за которое совершается одно полное колебание
Плотность жидкости определяется: ареометром
Поверхностное натяжение жидкости определяется: сталагмометром
Показатель преломления света определяется: рефрактометром
Потенциал измеряется в: вольт
Потенциал электрического поля определяется выражением: Ф=A|q
Потенциал электрического поля определяется выражением: “Фи” =a/q , здесь фи это потенциал электрического поля
Потенциал электрического поля является его: энергетической характеристикой
Поток магнитной индукции измеряется в: Вб
Прибор в котором при облучении поверности металлов светом возникает фотоэффект: фотоэлементом
Прибор для измерения активной электрической мощности: ваттметр
Прибор для измерения различных электрический величин наз: осциллографом
Прибор для регулирования силы тока и напряжения: реостат Прибор для наблюдения и измерения периферических величин называется: осциллограф Электрическое напряжение в цепи измеряется: вольтметром
Примером гармонических колебаний могут быть: колебания математического маятника
Сила взаимодействия неподвижных электрических зарядов определяется выражением: F=kq1q2/r в квадрате
Сила переменного тока изменяется по закону: синуса,косинуса
Сила перемещения тока измеряется по закону E=… /Mt
Сила тока определяется выражением: I=q|t
Сила электрического тока в цепи измеряется: амперметром
Согласно первому постулату Бора: электроны могут двигаться не по любым орбитам, а по орбитам вполне определенным
Согласно постулату Бора: движение электронов по стационарным орбитам не сопровождается излучением
Согласно постулату Бора: переход электрона с одной стационарной орбиты на другую, сопровождается поглощением или излучением
Сопротивление проводника цилиндрической формы определяется выражением: R=”ро”l|s
Центростремительной силой удерживающей электроны в орбите является: кулоновская сила
Частотой колебаний называется: величина,численно равная числу колебаний за единицу времени
Электрический ток в металлах определяется упорядоченным движением: электронов
Электромагнитное устройство преобр. параллельный ток одного напряжения и первый ток другого напряжения наз: трансформатором
Элементарными заряженными частицами являются: электроны и протоны (или просто протоны)
Эффективное “И”э и амплитуда “И”0 значение переменного тока соответственно: Иэ= И0/корень из 2
Явление дифракции выявляет свойства: волновые
Явление дифракции используется в: дифракционных решетках
Явление интерференции используется : в интерфераметрах
Явление интерференции используется в: интерферометрах
1. Задание {{ 1 }} ТЗ 1 Тема 1-1-0
Особенностью аморфных тел является их:
изотропность
- анизотропность
- упорядоченность структуры
- упругость
- пластичность
2. Задание {{ 2 }} ТЗ 2 Тема 1-1-0
Примером аморфного тела является:
- турмалин
- поваренная соль
- исландский шпат
стекло
- медь
3. Задание {{ 3 }} ТЗ 3 Тема 1-1-0
Особенностью кристаллических тел является:
- упругость
- изотропность
упорядоченность структуры
- пластичность
- ближний порядок
4. Задание {{ 4 }} ТЗ 4 Тема 1-1-0
Примером кристаллического тела является:
- стекло
поваренная соль
- янтарь
- пластмасса
- эбонит
5. Задание {{ 5 }} ТЗ 5 Тема 1-1-0
Явление полиморфизма вещества состоит в том, что оно:
- может обладать как изотропностью, так и анизотропией
- может находиться при некоторой температуре одновременно в нескольких агрегатных состояниях
может существовать в нескольких кристаллических модификациях, отличающихся физическими свойствами
- может существовать в нескольких агрегатных состояниях, отличающихся температурами
- может обладать структурами, характеризующимися как дальним, так и ближним порядком
6. Задание {{ 6 }} ТЗ 6 Тема 1-1-0
Полиморфным переходом называется переход:
- из одного агрегатного состояния в другое
- из изотропного состояния в анизотропное
- из кристаллического состояния в аморфное
- из аморфного состояния в кристаллическое
из одной кристаллической модификации в другую
7. Задание {{ 7 }} ТЗ 7 Тема 1-1-0
Структуры кристаллических решеток экспериментально изучаются с помощью:
дифракции рентгеновского излучения
- интерферометра
- поляриметра
- люминесцентного микроскопа
- фотоэлектроколориметра
8. Задание {{ 8 }} ТЗ 8 Тема 1-1-0
В объемноцентрированной кубической решетке частицы располагаются:
- только в вершинах куба
в вершинах куба и в его центре
- только в центре куба
- в вершинах куба и в центрах граней
- только в центрах граней
9. Задание {{ 9 }} ТЗ 9 Тема 1-1-0
В гранецентрированной кубической решетке частицы располагаются:
- в вершинах куба и в его центре
- только в вершинах куба
в вершинах куба и в центрах граней
- только в центре куба
- только в центрах граней
10. Задание {{ 10 }} ТЗ 10 Тема 1-1-0
В твердых телах частицы (молекулы, атомы, ионы):
- вращаются вокруг собственной оси
совершают тепловые колебания около положений равновесия
- движутся поступательно внутри твердого тела
- одновременно участвуют в поступательном и вращательном движении
- неподвижны
11. Задание {{ 15 }} ТЗ 15 Тема 1-1-0
Упругими называются деформации, которые:
- при снятии напряжения остаются постоянными
- не зависят от приложенного напряжения
при снятии напряжения практически полностью исчезают
- прямо пропорциональны приложенной силе
- обратно пропорциональны приложенной силе
12. Задание {{ 16 }} ТЗ 16 Тема 1-1-0
Пластическими называются деформации, при которых:
тело уже не восстанавливает свои первоначальные размеры и сохраняется остаточная деформация
- форма и размеры тела не зависят от приложенного напряжения
- напряжения при снятии деформирующей силы практически полностью исчезают
- напряжения прямо пропорциональны приложенной силе
- напряжения обратно пропорциональны приложенной силе
13. Задание {{ 19 }} ТЗ 19 Тема 1-2-0
Костная ткань в основном состоит из:
- окиси кальция
- коллагена
- гидроксилопатита
гидроксилопатита и коллагена
- фибрилл
14. Задание {{ 37 }} ТЗ 11 Тема 1-1-0
Отметьте правильный ответ
Относительным удлинением или относительной деформацией ε называется:
отношение
абсолютного удлинения Δl
к первоначальной длине l
образца

-
Отношение
первоначальной длины l
к абсолютному удлинению Δl
образца

-
Произведение
абсолютного удлинения Δl
на первоначальную длину l
образца

-
Величина

-
Величина

15. Задание {{ 38 }} ТЗ 12 тема 1-1-0
Механическим напряжением называется:
-
Отношение
площади S
сечения тела к модулю внешней силы F:

-
Отношение
абсолютного удлинения Δl
к первоначальной длине l
образца

Отношение
модуля внешней силы F
к площади S
сечения тела

-
Отношение
первоначальной длины l
к абсолютному удлинению Δl
образца

-
Величина

16. Задание {{ 39 }} ТЗ 13 Тема 1-1-0
Диаграммой растяжения называется графическое изображение зависимости между:
- ε и F
- σ и F
ε и σ
17. Задание {{ 40 }} ТЗ 14 Тема 1-1-0
Обозначая через Е модуль Юнга, закон Гука можно записать как:
-


-

-

-

18. Задание {{ 42 }} ТЗ 17 Тема 1-1-0
Обозначая через G модуль сдвига, относительную деформацию сдвига можно записать в виде:
-

-

-


-

19. Задание {{ 43 }} ТЗ 18 Тема 1-1-0
Обозначая через В модуль всестороннего сжатия, а через p - давление сжатия, относительную деформацию сжатия можно записать в виде:
-

-


-

-

