2. Распространение трещин при циклическом нагружении

При циклическом деформировании в гладком материале происходят процессы зарождения роста и объединения микротрещин, которые возникают вследствие определенных физических механизмов, связанных с перемещением и торможением дислокаций – линейных дефектов кристаллической решетки.

В материале с надрезом преимущественно развивается только одна трещина, зародившаяся от дна надреза, однако часто у ее вершины возникают микротрещины, они объединяются и приводят к окончательному разрушению.

В общем случае трещины классифицируются в зависимости от их размеров на малые и большие.

Малые трещины (МТ) (short cracks) в свою очередь делятся на два класса:

1. Микротрещины, размер которых сравним с размером структурных составляющих материала и соответствует 1...10 мкм;

б) физически малые трещины, развивающиеся в большинстве случаев в поверхностном слое и имеющие размеры 10² ... 10³ мкм.

Когда усталостные МТ, преодолев поверхностный слой, проникают вглубь материала, они переходят в разряд больших и развиваются далее как макротрещины. МТ размером 10 ... 10³ мкм называют еще микрометровыми.

Рассмотрим особенности распространения больших усталостных трещин, у которых напряженно-деформированное состояние в вершине характеризуется 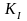, а предельная несущая способность (сопротивление хрупкому разрушению) – критическим значением КИН ( ). Наблюдаются три характерных этапа роста трещины (рис. 9.).

Первый из этих этапов характеризуется скачкообразным развитием трещины усталости. Ее возрастание происходит после некоторого периода накопления повреждений перед трещиной. Для многих сплавов, в частности алюминиевых и титановых, продвижения трещины усталости можно наблюдать на поверхности излома в виде полоски, борозды. На первом этапе ширина борозды не отвечает скорости роста трещины усталости за цикл.

Рис. 9. Диаграмма роста усталостных трещин

Второй этап характеризуется стабильным ростом трещины усталости с постепенным увеличением скорости. При этом наблюдается очень близкое соответствие между шириной борозды и продвижением трещины усталости за один цикл.

Третий этап – ускоренное возрастание трещины. Механизм разрушения смешанный – от усталости и квазистатический, который переходит в чисто статический. Завершающий этап – долом образца. Этот процесс есть уже не элементом процесса усталости, а лишь его завершением; долом может рассматриваться как статическое разрушение элемента, поврежденного трещиной. Но поскольку в ряде случаев характеристика долома (остаточная прочность) зависит от предыдущего процесса разрушения, этот последний акт разрушения усталости может рассматриваться и как последний этап развития трещины.

Наибольшее значение КИН, при котором усталостная трещина не распространяется или ее скорость меньше заданной, называется пороговым и обозначается 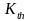. Кинетической характеристикой распространения является диаграмма роста усталостных трещин (ДРУТ) (рис 6.). ДРУТ получают экспериментально, при этом на оси ординат откладывается значения скорости роста трещин, а по оси абсцисс – значения максимального КИН в цикле ( ) или размах КИН ( ). ДРУТ слева ограничивается пороговым КИН , соответствующим моменту страгивания трещины или ее скорости не более 10^-10 м/цикл, справа – критическим КИН .

В аналитическом виде полную диаграмму роста усталостных трещин можно представить в виде

, (26)

где C и n – эмпирические коэффициенты.

Однако более широкое распространение получили зависимости, описывающие второй участок ДРУТ, который охватывает наиболее значительный диапазон скоростей роста трещин. Самым известным является уравнение Пэриса:

. (27)

Экспериментальные значения коэффициентов C и n уравнения (27) для некоторых типов сталей приведены в табл. 2.

Пэрис принимал n = 4, однако, как показали экспериментальные исследования, в том числе и представленные в табл. 2, .

Особое место занимает проблема роста малых усталостных трещин, для которых .

Таблица 2.

Значения коэффициентов C и уравнения Пэриса

Материал	Коэффициент асимметрии цикла, R	Температура испытаний, К	n	C
15Г2АФДпс	-1	293	2,55	1,110-9
  	-1	178	2,55	3,510-10
  	-1	153	2,6	3,6310-8
10ГН2МФА	-1	293	3,85	3,3910-12
  	-1	223	4,16	1,2610-12
  	-1	108	6,0	1,5810-16
  	-1	83	5,12	6,1710-15
15Х2МФА	0	623	2,55	1,6710-11
  	0	293	2,73	6,710-12
  	0	213	2,943	3,5810-12
  	0	183	3,521	6,110-13
15Х2НМФА	0	623	3,03	2,710-12
  	0	293	3,18	1,5510-12
  	0	213	3,66	3,1710-12
  	0	183	4,5	2,010-14
Армко-железо	-1	293	5,0	0,210-12
  	-1	83	5,374	1,7310-15
15Х3МА	0	293	2,822	4,2610-12
  	-1	293	2,473	2,210-11
  	0	213	3,206	1,9710-12
  	-1	213	2,8	4,610-12
  	0	183	3,454	1,7810-13
  	-1	153	5,14	7,57810-16