4.2. Механика усталостного разрушения
Одной из отличительных особенностей процесса развития трещины усталости является возможность оценки ее развития по изменению размера. Первый этап роста трещины можно считать и заключительным этапом ее образования.
На этапе образования образуется в результате объединения микротрещин под действием касательных напряжений. Процесс образования макротрещин отличается от процесса их дальнейшего развития, так как на первом этапе это трещины сдвига, которые потом развиваются как трещины нормального отрыва.
Рассмотренный этап (завершающий процесс микрорастрескивания при усталости и начальный для распространения макротрещин), изучен еще недостаточно. Этот этап уже можно анализировать методами механики разрушения, но в то же время процесс развития маленьких трещин существенно отличается от больших трещин. Очень часто в элементах с концентрацией напряжений на этом этапе развивается рядом несколько трещин, причем некоторые постепенно прекращают возрастать, а одна из них развивается в магистральную макротрещину.
Дальнейший процесс происходит в 3-4 этапа. Все они могут быть проанализированы методами механики разрушения, а определяющим фактором является величина напряжений растяжения.
Коэффициент интенсивности напряжений.
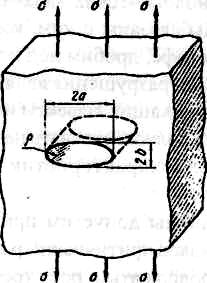
Для эллиптической
трещины с большой осью
и малой осью
(рис.6) максимальное напряжение у концов
главной оси равно
. (1)
–
приложенное
напряжение, направленное по нормали к
главной оси;
– половина главной оси;
– половина малой оси.
Радиус кривизны
у конца главной оси эллипса определяется
уравнением:
. (2)
|
Рис.
I. Эллиптическое отверстие
в бесконечно большой пластине
обусловливает возникновение концентрации
напряжений пропорциональной
|
Тогда, после объединения (1) и (2), получим
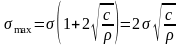при
. (3)
Концентрацию напряжений у трещины можно оценить с помощью соответствующего коэффициента:
. (4)
В декартовых
координатах с началом в вершине трещины
и осью
,
направленной вдоль большой полуоси
эллипса, распределение растягивающих
напряжений
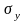для малых значений координаты
имеет вид
. (5)
При
из (5) следует выражение (3).
Для трещины с
острым кончиком (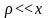
и
)
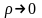формула (5) преобразуется в предельное
соотношение
, (6)
где параметр K называется коэффициентом интенсивности напряжений (КИН).
В общем случае КИН можно представить в виде
, (7)
где - коэффициент, учитывающий форму и размер образца, форму трещины, тип нагружения (изгиб, растяжение, сдвиг).
Величину КИН можно интерпретировать как степень высвобождения упругой энергии при разрушении.
Изложенные выше
положения справедливы для случая
идеального упругого деформирования
материала в области, примыкающей к
трещине. Однако значительная концентрация
напряжений (при
,
)
должна приводить в реальных материалах
к локальному пластическому деформированию,
когда локальные растягивающие напряжения
у кончика трещины превысят предел
текучести:
(рис.2 и 3).
Рис.2. Пластическое деформирование у кончика трещины.
Рис.3. Размеры пластической зоны (затемненная область) при разрушении по хрупкому и вязкому механизмам.
Размер зоны пластического деформирования (ЗПД) s в направлении оси x можно оценить по формуле
. (14)
Оценка (14) является заниженной. С учетом перераспределения напряжений в ЗПД ее длину увеличивают в два раза и в расчетах пользуются формулой
(15)
Более точную оценку
величины размера s
дает модель Дагдайла - Баренблатта.
Предполагается, что длина трещины
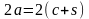и что существуют напряжения, стремящиеся
захлопнуть трещину на участке
(рис. 4).
|
Рис. 4. Модель упругой трещины для определения размера ЗПД. |
Предполагается
также, что эти напряжения близки по
значению к пределу текучести материала
в идеально пластичном теле и действуют
в локальной зоне пластического
деформирования. Из условия равновесия
гипотетической трещины с полудлиной
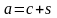при
(отсутствуют
особенности в распределении напряжений
у вершины) получено
. (16)
При
уравнение (16) приобретает вид
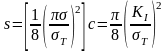. (17)