Формулировка критерия Михайлова.

Система будет устойчивой, если годограф Михайлова, начиная с действит. полож. Полуоси, с ростом

числа w, огибает против часовой стрелки начало координат, проходя при этом последовательно столько квадратов, каков порядок D(p) хар. Уравнения

ПРИМЕР

D(p): 2p³+3p²+3p+1=0

2 (iw)³+3(iw)²+3iw+1=0

W	0	1	2	∞
U(w)	1	-2	-11	-∞
ϑ(w)	0	1	-10	-∞

мн.ч д. ч мн.ч д.ч

U(w)=1-3w²

ϑ(w)=3iw-2iw³=(3w-2w³)i

ϑ(w)

II 1 I

-11

-2 0 1 U(w)

-11

III IV

Ответ: система устойчива

Второй способ построения:

При практ. построении Годографа Михайлова сначала определяют точки пересечения годографа с координатными осями.

Для этого сначала решают уравнение U(w)=0 и определяются частоты соответствующие точкам пересечения годографа с мнимой осью. Их подставляют в уравнение ϑ(w) для определения соответствующих координат.

Аналогично определяются точки пересечения с действительной осью.

ПРИМЕР

D(p):p³+4p²+9p+1=0

U(w)=1-4w²

ϑ(w)=9iw-iw³

a) 1-4w²=0

4w²=1

W²=1/4 Wϵ[0;+∞]

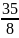W _1,2= ± = ± 0,5 ϑ(w)

W₂ ϵ [0;+∞); W₁= 2 1

U ( )=9*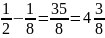 0 U(w)

-35 3

б) 9w-w³=0

w(9-w²)=0

w=0; 9-w²=0

w₁₂=±3; w₂=+3

U(0)=1

U(3)=-35

w	0		3
u	1	0	-35
ϑ	0		0

О твет: Система устойчива n=2 ϑ n=5

U

0

n=3 n=3

на грани устойчивости

Следствие критерия Михайлова:

Система устойчива, если годограф Михайлова поочерёдно пересекает действительную и мнимую оси. Следовательно, необходимо и достаточно, чтобы точка пересечения годографа положительной и отрицательной оси передавались.

Амплитудно-фазные критерии Найквиста.

Критерий Найквиста позволяет оценить устойчивость замкнутой системы по характеристикам разомкнутой системы.

W₁(p)

W₂(p)

W₃(p)

Разомкнутая

W_раз=

W₁(p)

W₂(p)

W₃(p)

Замкнутая

W_зам=

Разомкнутая система может быть в 3х состояниях: устойчивой, неустойчивое, нейтральное. В зависимости от этого буде меняться формулировка критерия Найквиста:

Случай 1. Система разомкнутая, устойчивая.

Если разомкнутая система устойчива, то замкнутая система будет устойчива в том случае, если годограф АФХ разомкнутой системы не охватывает точку Е с координатами Е(-1;0)

Если охватит точку (-1;0), то замкнутая система неустойчива

U

Е(-1;0)

Случай 2. Разомкнутая система неустойчивая.

Если разомкнутая система неустойчивая, то для устойчивости замкнутой системы необходимо, чтобы АФХ разомкнутой системы охватывала точку (-1;0) столько раз, сколько правых корней у РС.