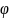Автоматическое управление.
Управление-совместимость действий, осуществляемых на основании определённой информации и направленных на поддержание или улучшения функций объекта в соответствии с целью управления.
Автоматическое управление – управление, которое осуществляется без участия человека.
Регулирование- частный случай управления, при котором технологические параметры поддерживаются на заданном значении с помощью специальных устройств автоматических регуляторов.
Структурная реализация принципов управления. Существуют разомкнутые системы автоматического регулирования, разомкнутые системы просты, но не точны. В ряде случаев Δ при объектов с запаздыванием, они имеют преимущества перед замкнутыми системами по быстродействию.
Замкнутые системы позволяют получить хорошую точность и быстродействие, но при неправильной настройке может потерять устойчивость, т.е. перестают решать требуемую задачу.
Разомкнутая САР с жёстким управлением.
X o(t)- возмущающее действие. Хb(t)
Х
ОУ

 з
з

Регулятор
(t) U(t) y(t)
U(t)-управляющее воздействие; ХВ(t)- возмущающее воздействие.
Задание Хз(t)- функция времени, определяющая как должна вести себя управляемая величина y(t).
Данная схема может быть применена тогда, когда возмущающая величина ≈0 (ХВ≈0) или когда ХВ(t) может быть предвычеслено с достаточной точностью и предварительно учтено в задании.
ХЗ – задающая величина.
Разомкнутая САР с управлением по отклонению.
ХB(t)
Х


 з(t)
з(t)
Ʃ
Р
ОУ
E(t) y(t)
+ - ОС
Схема исполнения для слежения программы управления и стабилизирующий. В такой системе регулятор в процессе управления учитывает как задание, так и реальное состояние объекта, а кроме того косвенно учитывает возмущение, здесь Е(t)- отклонение ( ошибка регулирования), отклонение Е(t)= XЗ -y(t)
Разомкнутая САР с управлением по возмущению.
 ХB(t)
ХB(t)
Х
Регулятор
ОУ
з (t) U(t) y(t)
Сравнивающее устройство сравнивает заданные и управляемые величины и вычитает Е(t).
Регулятор вырабатывает управляющее воздействие U(t), которое сводит отключение к О или к допустимому минимуму.
Комбинированная схема с управление по отклонению и возмущению.

 ХB(t)
ХB(t)
Х з(t)
Ʃ
Р
ОУ
E(t) U(t) y(t)
+ - ОС
Эта схема обладает наилучшими свойствами и чаще других используется для слежения и стабилизации, и программного управления при решении задач, в которых требуется получить высокую точность и быстродействие.
Виды регулирования:
По отклонению:
“+”: регулятор не зависимо от вида, числа и места приложения возмущающих воздействий при наличии отклонения вырабатывает регулирующее воздействие.
“-“: необходимость наличия отклонения.
По возмущению:
“+”: возмущающее воздействие компенсируется до входа в объект регулирования.
“-“: необходимо иметь столько регуляторов, сколько возмущающих воздействий.
Комбинированный:
“+”: улучшенное качество регулирования.
Основные требования, предъявляемые к САР.
Основной задачей является поддержание регулируемой величины на заданном значении САР д. б.
Устойчивой
Отвечать требованиям качества регулирования.
САР называется устойчивой, если после вывода её из равновесного состояния, она снова возвращается в свое равновесное состояние или новое равновесное состояние.
Классификация САР
По принципу работы САР
А) стабилизирующая – значение регулируемой величины постоянно поддерживается на заданном значении.
Б) программная – регулируемая величина регулируется по заранее заданной программе.
В) следящая – значение регулируемой величины сравнивается со значением другой величины и между ними устанавливается определённое соотношение.
Г) система экстремального регулирования – значение регулируемой величины поддерживается на max или min возможном значении.
2. По виду энергии, применяемой для реализации регулирующего воздействия.
А) система прямого действия – для реализации регулирующего воздействия используется энергия измеряемой среды.
Б) система непрямого действия- для реализации регулирующего воздействия используется энергия подводится извне.
Типовые элементарные звенья. Свойства, характеристики звеньев и систем.
Линейные объекты с сосредоточенными параметрами описываются дифференциальном уравнением вида
an y(n)(t)+an-1y(n-1)(t)+…+a1y’(t)+a0y(t)=bmxm(t)+bm-1xm-1(t)+…+b1x’(t)+b0x(t)
a0-an и b0-b1 характеризуют конструктивные параметры объекта, физико – химические свойства вещества. Для стационарных систем коэффициенты дифференциального уравнения постоянны.
Разделив обе части уравнения на коэффициент a0, получим коэффициенты, которые имеют размерность времени и называются постоянными времени.
Tn y (t) + Tn y(n-1) (t) + … + y( t) = Tm x(m) (t) + Tm-1 x(m-1) (t)+ … +k x(t)
[T]= с
Дифференциальные уравнения описывает поведение объекта в переходных режимах при любых измерениях входной величины.
В автоматическом управлении (АУ) часто используются сигналы, имеющие разрыв в начальный момент времени. В связи с этим для характеристики динамических свойств линейных объектов широко используется переходные процессы, соответствующие типовым входным сигналам.
Такими являются кривая разгона и импульсная переходная функция.
Преобразование Лапласа.
В АУ широко используется метод прикладного анализа, в основе которого лежит метод Лапласа. Преобразования по Лапласу ф. называется ф. комплексной переменной и опр-ся соответствующем
X(p)=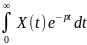
X(t)-оригинальная ф.; X(p)-изображение.
![]() {x(t)}=x(p)
{x(t)}=x(p)
1.Линейная операция
{x1(t)+x2(t)}= {x1(t)}+ {x2(t)}
2. Дифференциалу оригинала соответствует умножение изображения на множитель p
{x’(t)}= p*x(p)
3. Интегралу оригинала соответствует деление изображения на p
{
4. Теорема запаздывания
![]()
 {x(t-
)}=x(p)*e-pt
t-
Ƭ=U0
{x(t-
)}=x(p)*e-pt
t-
Ƭ=U0
{x(t-
Ƭ)}=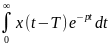 =
t=U+
Ƭ =
=
t=U+
Ƭ =
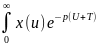 du=
du=
dt= du
=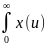 *e-pu
e-pt
du=e-pt
e-pu
du=
e-pƬ
*e-pu
e-pt
du=e-pt
e-pu
du=
e-pƬ
 e-p(t-
Ƭ)
e-p(t-
Ƭ)
d(t-Ƭ)=e-pƬ*x(p)
5. Теорема свёртывания.
{x1(t)*x2(t)}=x1(p)*x2(p)
6. Теорема о конечном значении функции:

7. Теорема о начальном значении функции:
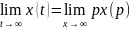
Передаточные функции.
Одной из основных характеристик элемента САУ является передаточная функция – отношение преобразованного по Лапласу выходной сигнал к преобразованному по Лапласу Входному сигналу при нулевых начальных условиях.
W(p)=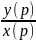
Если ОУ имеет несколько входных сигналов, то каждому каналу связи будет соответствовать своя калибраточная функция.
W1(p)
W2(p)
W3(p)
X1(p)
 X2(p)
y(tp)
X2(p)
y(tp)
X3(p)
В общем случае динамика объекта по каждому каналу описывается с помощью ДУ:
any(n)(t)+an-1y(n-1)(t)+…+a1y’(t)+a0y(t)=bnx(m)+bm-1x(m-1)(t)+…+b1x’(t)+b0x(t)
Преобразуем по Лапласу и получим
anpn*y(p)+an-1pn-1y(p)+…+a1py(p)+a0y(p)=bmpmx(p)+bm-1pm-1x(p)+
+…+b1px(p)+b0x(p)
Y(p)(anpn+an-1pn-1+…+a0)=x(p)(bmpm+…+b1p+b0)
О
W(p)=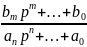
Для реальных объектов степень полинома числителя дроби меньше или равна степени полинома знаменателя.
Из передаточной функции также можно определить специальные динамические характеристики звена, позволяющие оценить его поведение при любых входных сигналах:
Полюсами обозначены p* называется корень уравнения, стоящего в знаменателе.
Нулями Р0называется корень уравнения, стоящего в знаменателе.
Пример
2y’(t)+y(t)=5x(t); W(p)-?
2y(p)*p+y(p)=5x(p); p*, P0-?
Y(p)(2p+1)=5x(p)
= =W(p)
=W(p)
2p+1=0 5≠0
P*=-0,5
Ответ:
W(p)=
;
P*=-0,5; p0≠y(t)+2y”(t)+y’(t)=5 W(p)-?
W(p)-?
2y(p)*P2+Y(p)*p+y(p)=5x(p)/p
Y(p)(2*p2+p+1)=5x(p)/p
=
2p2+p+1=0 и p3*=0
D=1-8=-7
P1=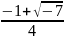 =
= +i
+i
P2=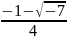 = –
= –
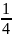 – i
– i
Ответ: p*=0, + i ; – i ;
Временные характеристики.
Динамические свойства линейных звеньев (объектов) могут быть описаны дифференциальным уравнением или представлены графическими характеристиками.
Применяют 2 типа таких характеристик:
1. Временные (переходные)
2. Частотные
Переходные характеристика - динамическая характеристика используется для описания одноканальных объектов с нулевыми начальными условиями.
Дифференциальные уравнения общего вида:
any(n)+an-1Y(n-1)+…+a1y’+a0y=bmUm+…+b0u
y(0)=0;y’(0)=0; y(n-1)(0)=0
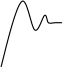
Переходной характеристикой(функцией) h(t) называется реакция системы на единичное ступенчатое воздействие
x


1
1(t- )
 t
t
y
t
Для анализа определяется переходная функция, следует решить дифференциальное уравнение при нулевых начальных значениях и единичном входном воздействии.
Единичная ступенчатая функция- обладает свойствами

1(t- )=
 0, при t<
0, при t<
1, при t≥
Уравнение , описывающее переходный процесс в элементе САУ при скачкообразном входном воздействии называется уравнением кривой разгона, а его график- кривой разгона
Импульсная переходная функция(характеристика) обозначается g(t), представлет собой реакцию на входное воздействие типа единичной импульсной функции при нулевых начальных условиях
δ
 (t-
)= 0, при t=
(t-
)= 0, при t=
∞, при t=
x
 1
1
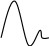
t
y
t
С помощью дельта – функции δ(t- )) можно описать реальное входное воздействие типа удара.
Переходная характеристика и импульсная переходная функция связаны между собой соотношениями.
g(t)=h’(t)
h
(t)=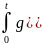 ) d
) d
Частотные характеристики (ЧХ).
ЧХ описывают установившиеся вынужденные колебания, вызванные гармоническим воздействием на входе.
Гармоничные воздействия представляют собой синусоиду
X
объект
=a sin (ωt+ϕx) y=B sin (ωt+ϕx)
Пусть на вход звена подается гармоничное воздействие x(t)=Авхsin(ωt+ϕвх)
А-амплитуда
ω-угловая частота
φ- фазовый сдвиг
По окончании переходного процесса на выходе объекта также установится гармонические колебания с той же частотой, но отличающиеся по амплитуде и по фазовому сдвигу.
Y(t)=Aвыхsin(ωt+ϕвых)
Степень различия между сигналами на входе и на выходе позволила выбрать в качестве частотных следующие характеристики:
1. Амплитудно-частотная характеристика (АЧХ):
А(ω)=

2. Фазо-частотные характеристики ФЧХ: ϕ(ω)=ϕвых(ω)-ϕвх(ω)
Это зависимость разности между фазовым сдвигом на выходе и фазовым сдвигом на входе от частоты.
3. АФХ- это комплексная функция, для которой АЧХ является модулем, а ФЧХ – аргументом
W(iω)=A(ω)*eiφ(ω)
Такие можно определить по передаточной функции частотной характеристики объектов.
Для того, чтобы найти АХ, нужно в передаточной функции p заменить на iω
АЧХ:
A(ω)=
ФЧХ: ϕ(ω)=arg(W(iω))
Такие АФХ могут быть предварительно в прямоугольных координатах
W(iω)=U(ω)+iϑ(ω)
Связь между полярными и Декартовыми координатами(x, y)
A
A=a
 =a
=a
B=b+ic
 =
=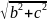
C=ic
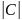 =c
=c
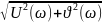
ϕ
iϑ (Компл.)
(ω)=arctg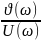
В
c
U(действ.)
А
arg(A)=0
arg(B)=arctg
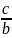
arg(C)=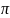 /2
/2
Пример. Рассмотрим график АФХ называемым годографом
 =1
=1
arg(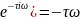
Пример.
Требуется построить частотные
характеристики объектов, передаточный
функции, которая имеет вид W(p)= ;
;
W( =
=
A(

|
0 |
2 |
|
A |
1 |
|
0 |
|
0 |
-… |
- |

U

Пример
2. W(p)=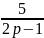
W(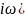 =
=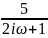
A(
)=
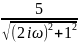
(
)=0-arctg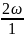
|
0 |
|
A |
5 |
0 |
|
0 |
|
A



5
5
0
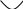
U
Типовые динамические звенья.
Статические звенья.
У статических звеньев в установленном режиме выходная координата пропорционально входной, поэтому в статике все статические звенья описываются уравнением:
Y=k*x
1. Идеальное статическое звено(усилительное)- это звено и в статике, и в динамике описывается уравнением
1) Y(t)=k*x(t); k- коэффициент усиления звена
2) W(p)= =k передаточная функция.
3
t
t
U
1
h
k
Времен. хар.
)
а) Переход. хар.
D(p)=p3+2p2+4p+1=0
б
X
) Импульсная характеристика g(t)=k*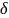 (t)
(t)
1


k
g
t
t
n(t)=k*i(t)
4) Частотные характеристики
W( )=k
A( )=k
A
k



h U
0
Т.к. частотные характеристики не зависят от частоты, то следовательно усилительное звено не меняет свою фазу входного сигнала, изменяет его по амплитуде в K раз.
2. Статическое
звено
 порядка (апериодическое).
порядка (апериодическое).
1) Дифференциальное уравнение T*y’(t)+y(t)=ku(t)
2) Передаточная функция Tp*y(p)+y(p)=ku(p)
y(p)[Tp+1]=ku(p)
W(p)=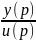 =
=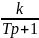
3
U
1
Y
k
) Переходная функция h(t)=k(1-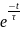 )
)

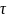
Импульсная переходная функция.
G(t)=h’(t)=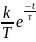
U
y
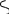

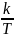
 t
T
t
t
T
t
Если эти характеристики получены экспериментально, то значит Т и К можно получить, как показано на рис.
4) Частотные характеристики АФХ
W(iω)= ;
A(ω)=
;
A(ω)=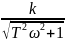
( )=-arctg T
АЧХ ФЧХ
А

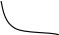 К
К
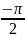
А
 ФХ
ФХ
u U
0
Примеры апериодических звеньев:
1. Генераторы постоянного тока
2. Двигатели любого типа
3. Резервуар с газом или жидкостью
4. Нагреватели печь, термопары.
3. Статическое
звено
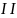 порядка (колебательное)
порядка (колебательное)
1) T22 y”(t)+T1y’(t)+y(t)=KU(t) дифференциальное уравнение.
2)
Передаточная функция. W(p)=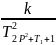
3
 )
Временная характеристика
y
)
Временная характеристика
y
U k
1 Перех. хар. Имп. переход. хар.
t t
4) АФХ. Частотные характеристики.
W(
)=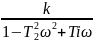
A(
)= АЧХ
АЧХ
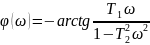 ФЧХ
ФЧХ
 АЧХ
ФЧХ
t
АЧХ
ФЧХ
t
A
 -
-
K ω -
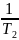 АФХ
АФХ
 K
U
K
U
Как видно из формулы, на малых частотах появляется некоторый рост АЧХ. Характеристика max значении на частоте = .
4. Статическое звено II порядка(апериодическое)
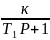
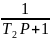
Это звено представляет собой цепочку из 2х апериодических звеньев I порядка.
1)
2
)W(p)=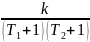
3) U
 1
k
1
k
h t t
h(t)=C0+C1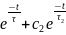
C0=k
C1=
C2=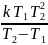
ИПФ:
g(t)=
-
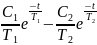
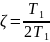 – коэффициент демпфирования.
– коэффициент демпфирования.
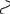 U
g
U
g

t t
Апер. II
пор
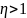
Колеб. II
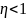
4) Частотные характеристики.
W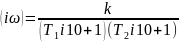
A




 А
А
k

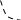

K u
Интегрирующие звенья.
1
 .
Идеальное интегр. звено.
g
.
Идеальное интегр. звено.
g
1 ) y(t)= kx(t) h k
2
)
W(p)=
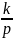 3) h(t)=kt
t
t
3) h(t)=kt
t
t
4)
W(
)=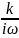 g(t)=k
g(t)=k
A(
)=
- arctg( )=
-
)=
-
 A
i
A
i U
U
 w=+∞U
w=+∞U
W W Iw=0
2 . Интегральное звено с запаздыванием. h Kt
1) Ty”(t)+y’(t)=ku(t)
2
t
) W(p)=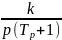
3
T
g
 )
h(t)=k[t-T(1-
)
h(t)=k[t-T(1-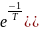 *1(t)
T
*1(t)
T
K
g(t)=k(1-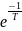 )
)
t
4)
W(
)=
A(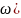 =
=
 w
w

 A
A
W
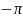
 U
U
3. Дифференцирующие звенья
3.1 Идеальное дифференциальное звено
1) y(t)=kx’(t) по этому уравнению определить частотные характеристики и периодическую функцию
y(p)=kpx(p)
2)
W(p)=
4) W( )=k
A( )=k
A(
)=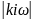 =k
=k
A
 (
)=arg(
(
)=arg(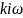 )=arctg(-∞)=
iw АФХ
)=arctg(-∞)=
iw АФХ
U
0 W
0 W
3) Временная характеристика
H(t)=k*1’(t)=K (t)
h
t
3.2. Дифференцирующее звено с запаздыванием.
1) Ty’(t)+y(t)=kx(t)
Tpy(p)=y(p)=kpx(p)
2)
W(p)=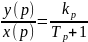
3)
h(t)=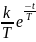 g(t)=h’(t)=
g(t)=h’(t)=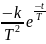
H g


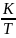 t
t
t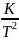
4)A(
)=
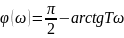

 h
h
iw

Структурный метод.
Структурная схема- графическая модель системы, в котором каждому элементу ставится в соответствие его динамической характеристикой. Она наглядно отражает состав системы и связи между её составляющими.
Структурная схема может быть построена на основе как дифференциальное уравнение, так и передаточной функции.
Любая сложная структурная схема может быть изображена с помощью основных типов соединений:
1. Параллельное соединение.
2. Последовательное
3. Соединение с обратной связью
Структурные схемы
1. Параллельное соединение звеньев .
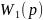


x y2 y
y3
y=y1+y2+y3
yi(p)=x(p)*Wi(p)
y(p)=
Эквивалент передаточной функции Wэкв = сумма всех передаточных функций
Wэкв(p)=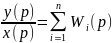
Wэкв
X y
2. Последовательное соединение звеньев.
x
W1(p)
W2(p)
W3(p)
y1 y2 y
y1(p)=W1(p)*x(p)
y2(p)=W2(p)*x(p)*W1(p); y2(p)=y1(p)*W2(p)
…
Yn(p)=Wn(p)*yn-1
Y(p)=W1(p)*W2(p)*…*Wn(p)*x(p)
Wэкв= Wi(p)
Wi(p)
3. Соединение с обратной связью.
Обратная
связь-передача сигнала с выходом сигнала
 на
его вход.
на
его вход.
X
Wп(p)
y 
Wоб(p)
Обратная связь может быть положительной. При этом E=X+Yос
или отрицательная. При этом E=X-Yос

Wэкв=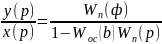 для ПОС
для ПОС
Wэкв= для ООС
для ООС
+
Y(p)=E*Wп(p)
E=x+ yос
Yос=y(p)Wос
Y(p)=(x(p)+Yос)*Wп(p)
Y(p)=(x(p)+y(p)Wос*Wп(p)
Y(p)=x(p)*Wп(p)+y(p)Wос*Wп(p)
y(p)-y(p)Wос(p)Wп(p)=x(p)Wп(p)
y(p)-y(p)Wос(p)Wп(p)=X(p)Wп(p)
y(p)(1-WосWп)=X(p)Wп
Привила преобразования в структурных схемах.
1. Перенос узла через узел осуществляется без дополнительных преобразований
X (1) (2) X X (1) (2) X
X X X X
2. Перенос сумматора через сумматор осуществляется без дополнительных преобразований



 X1+X2
X1+X3
X1+X2
X1+X3
X2 X3 X3 X3
3. Перенос узла через сумматор
X1
X1+X2
X1 X1+X2

X2 X1
X2 X1+X2
X2
X1 X2![]()
4. Перенос сумматора через узел.

 X
X1+X2
X1
X1+X2
X
X1+X2
X1
X1+X2
X1

X1+X2
X2 X1+X2 X2
5. Перенос узла через звено
W
W
X XW X XW
1/W
X
X
6
W
. Перенос звена через узел
W
X XW X XW
W
XW
XW
7. Перенос сумматора через звено
X
W
W

W
1 (X1+X2)W X1 X1W X1W+X2W=(X1+X2)WX2 X2W
X2
8. Перенос звена через сумматор
W


W
X1 X1W+X2 X1 X1+X2/W X1W+X2X2/W
1/W
X2
X2
9
W1
W2
. Перенос звена через звеноX
W2
W1
XW1W2 X XW1W2
1
W1
0. Переход к единичной обр. связью 
W2
1/ W1

W2
W1
X g
Wэкв=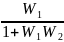 Wэкв=
Wэкв=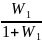 для единич. ОС
для единич. ОС
Пример1.
![]()
K/P
K1
Wэкв-?
Wэкв=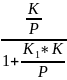 =
=
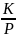 : (1+
: (1+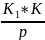 )=
:
)=
:
 =
=
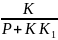
Wэкв =
=

Y(p) = X(p)
Y(p)*(p+KK1)=x(p)K
P *y(p)+KK1*y(p)=KX(p) y’(t)+KK1y(t)=KX(t)
Устойчивость лин. Системы
Устойчивость – способность системы возвращаться к состоянию установи установившегося равновесия после снятия возмущения, нарушавшем это равновесие.
Неустойчивая система непрерывно удаляется от состояния равновесия или совершает вокруг него колебания с увеличивающейся амплитудой.
Существуют также нейтральные системы, которые после снятия возмущения переходят в состояние равновесия, отличное от исходного.






1- уст. 2- неуст 3- нейтрал.
 1
1
y

 y
y
1
t t
2
2
Рис. 1 Рис. 2
Если система не устойчива (Рис. 1), то достаточно любого толчка, что бы в ней начался расходящийся процесс (1- апериодический; 2- колебательный)
Апериодически расходящийся процесс могут возникнуть в Δ в САР, если в ней ошибочно переключить на управляющем устройстве полярность воздействия на объект. В результате чего управляющее устройство будет осуществлять не отрицательную, а положительную ОС., т.е. не устранять, а увеличивать отклонение.
Колебат. расходящийся процессы могут возникнуть, если установить слишком большой коэффициент усиления на УУ.