14.2. Существование решения нелинейных уравнений установившегося режима

Обусловленность матриц характеризуется числами обусловленности [3]. Одно из чисел обусловленности равно отношению наибольшего и наименьшего по модулю собственных значений матрицы. Непосредственный расчет этих чисел трудоемок. Элементы матрицы производных уравнений установившегося режима (матрица Якоби) зависят как от параметров сети, так и от параметров режима. Поэтому плохая обусловленность матрицы Якоби может быть следствием как сильного различия (неоднородности) параметров сети, так и близости рассчитываемого режима к предельному по существованию или апериодической статической устойчивости.

Неоднородность электрической сети велика, если имеются устройства продольной компенсации, шиносоединительные выключатели либо близкие к нулю сопротивления обмотки среднего напряжения трехобмоточных трансформаторов и автотрансформаторов. В этих случаях плохо обусловлена как матрица , так и матрица Якоби. Как правило, плохая обусловленность матрицы может характеризоваться относительной малостью определителя. Близость режима к предельному по существованию или по апериодической статической устойчивости [3] соответствует приближению к нулю якобиана, то есть определителя матрицы Якоби уравнений установившегося режима, и плохой обусловленности матрицы Якоби [3].

При задании активных мощностей и модулей напряжений в генераторных узлах при сформулированных в [3] допущениях якобиан уравнений установившегося режима совпадает со свободным членом характеристического уравнения и прохождение якобиана через нуль соответствует пределу по апериодической устойчивости. Поэтому в данном случае приближение к нулю якобиана соответствует приближению к пределу по апериодической устойчивости.

Как правило, приближение к нулю якобиана соответствует ухудшению обусловленности матрицы . Строго говоря, величина определителя не всегда характеризует обусловленность. В тех случаях, когда наибольшее по модулю собственное число матрицы остается конечным, приближение к нулю якобиана соответствует резкому ухудшению обусловленности.

Сходимость решения нелинейных уравнений установив­шегося режима связана с величиной якобиана системы уравнений установившегося режима, т.е. с условиями существования и единственности. Последние используется при расчетах режимов близких к пределу по апериодической устойчивости. Если якобиан равен нулю в точке решения , то методы простой итерации или Зейделя не сойдутся при решении системы уравнений установившегося режима.

14.3. Существование решения нелинейных уравнений установившегося режима

Существование решения поясним на примере уравнения установившегося режима линии только с реактивным сопротивлением х , изображенной на рис 14.2, а.

2

4

90^{0 5}

3

1

0 a b P

б)

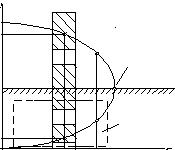
Рис 14.2. Существование и единственность решения установившегося режима:

а – линия с реактивным сопротивлением; б – определение установившегося режима.

Уравнение установившегося режима — это уравнение мощности, передаваемой по линии [3]:

, (14.10)

где - модули напряжений в узлах 1 и 2;

Р - мощность, текущая по линии, потребляемая в узле 2 и генерируемая в узле 1;

- фаза напряжения в узле 2.

При , предел передаваемой мощности – постоянная величина:

, (14.11)

и уравнение (14.111) имеет следующий вид:

. (14.12)

Для удобства направим активную мощность по горизонтальной оси, а угол - по вертикальной (рис.14.2, б). Найти решение уравнения установившегося режима - это значит для любого значения мощности найти соответствующее ему значение угла . Геометрически на рис.14.2, б решение соответствует пересечению прямой, параллельной оси Р (то есть прямой P = const), с синусоидой. Например, при Р = Р₂ = const решение соответствует точке 1 с координатами Р₂, или точке 2 с координатами Р₂ и .

Рассмотрим прямоугольную область , , заштрихованную на рис.14.2, б вокруг точки 1. Решение уравнения установившегося режима существует в этой области, если для каждого значения Р в интервале [а, b] существует одно или несколько значений , которые совместно с Р удовлетворяют уравнению (14.12).

Геометрически существование решения для всех Р в прямоугольнике , означает, что любая прямая в этом прямоугольнике, параллельная оси , пересечет синусоиду хотя бы один раз внутри этого прямоугольника. Аналогичное решение существует внутри прямоугольника , , заштрихованного на рис.14.2, б вокруг точки 2. Внутри же прямоугольника , не существует решения уравнений установившегося режима. В этом прямоугольнике ни одна прямая Р= const не пересекает кривую уравнения установившегося режима (14.10) [3].

Решение существует для любого положительного значения мощности, которая меньше, чем предел передаваемой по линии мощности . Для мощности решение уравнения установившегося режима не существует. Физически несуществование решения означает, что по линии с сопротивлением х при модулях напряжений на концах линии , нельзя передать мощность больше предела передаваемой мощности , который определяется выражением (14.11).

Нелинейные уравнения установившегося режима можно записать в виде системы неявных функций:

(14.13)

где Y - вектор независимых переменных (регулируемых параметров режима);

X - вектор зависимых переменных (нерегулируемых параметров режима);

W - вектор-функция, например небалансов мощности или тока в узлах.

Размерность вектор-функции равна размерности вектора X.

Существование решения в общем виде, то есть для уравнений (14.13), состоит в следующем. Существование решений уравнений установившегося режима при заданном значении вектора независимых переменных означает, что имеется хотя бы одно значение вектора зависимых переменных - такое, что параметры режима удовлетворяют уравнениям установившегося режима.