9.3. Уравнения узловых напряжений при напряжении балансирующего узла

Для сети постоянного тока из четырех узлов можно записать в следующем виде [3]:

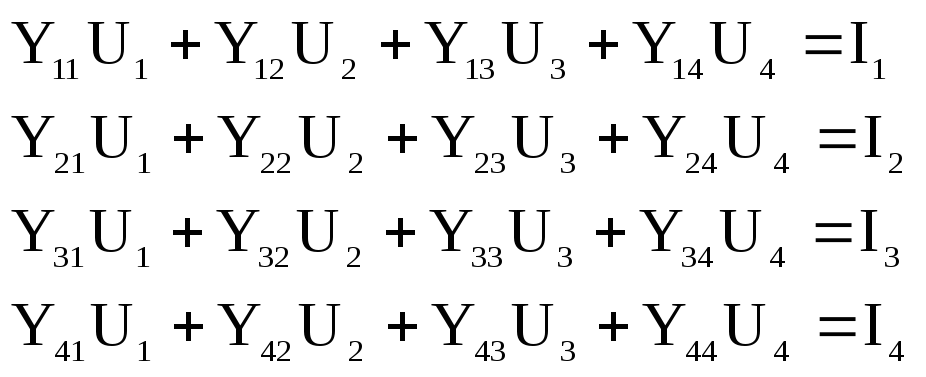
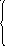. (9.13)

Полная система уравнений узловых напряжений, аналогичная (9.1), может быть записана в матричном виде для сети постоянного тока из (n + 1)-го узла следующим образом:

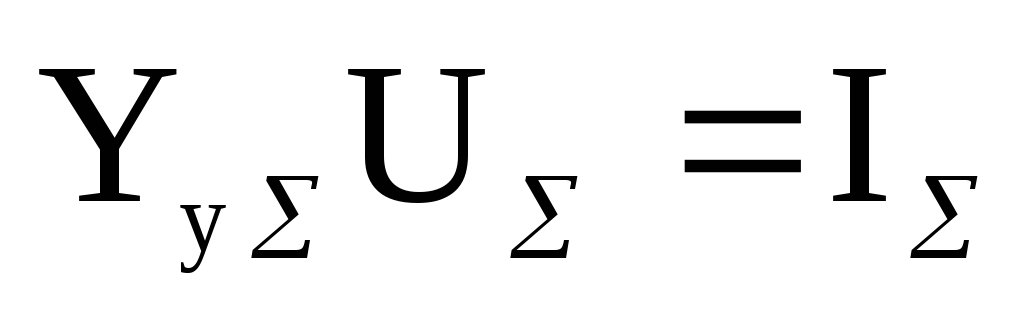, (9.14)

где - полная матрица узловых проводимостей порядка (n + 1);

, - вектор-столбцы токов в узлах и напряжений узлов порядка (n + 1).

Сумма всех токов в узлах равна нулю. Полная матрица узловых проводимостей является симметричной и вырожденной, если не учитываются проводимости на землю.

Вырожденность полной матрицы следует, например, из (9.13) Полная система уравнений узловых напряжений (9.13) или (9.14) линейно зависима; независимыми являются лишь n уравнений.

Уравнения (9.13) или (9.14) решаются обычно следующим образом. Один из узлов системы, например (n + 1)-й, принимается за балансирующий. Напряжение в этом узле предполагается известным, а ток равен сумме токов остальных n узлов. Токи в остальных n узлах заданы, а напряжения неизвестны. Вместо вырожденной системы с полной матрицей (9.14) или (9.13) решается система n независимых уравнений узловых напряжений с неполной матрицей :

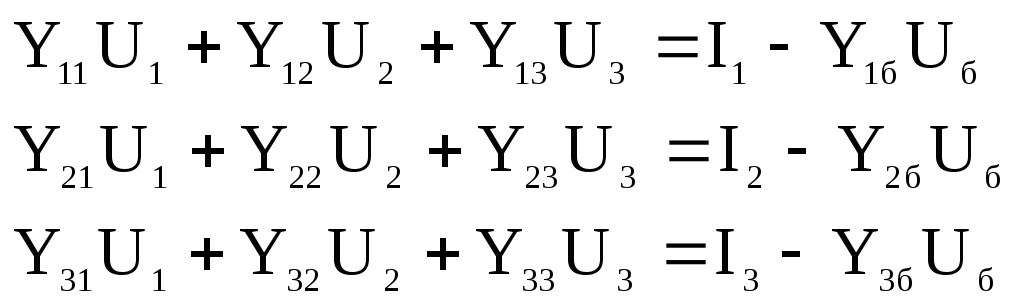
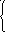. (9.15)

или в матричном виде

. (9.16)

где вектор-столбец равен:

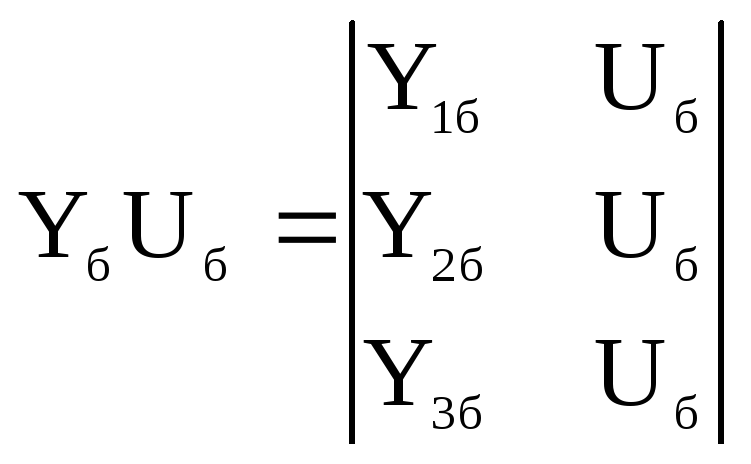. (9.17)

Если в системе уравнений узловых напряжений учесть, что в соответствии с (9.3) равно:

, (9.18)

то (9.16) можно переписать в виде:

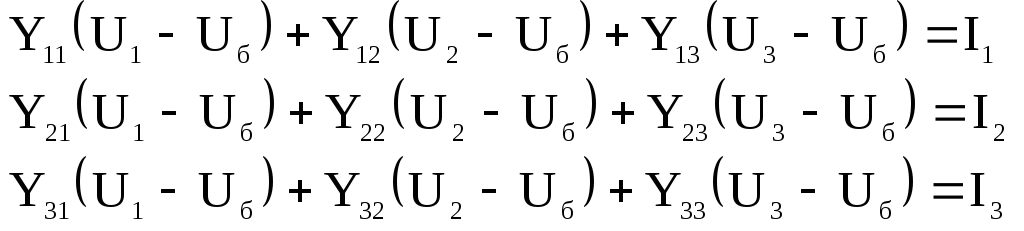
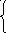. (9.19)

Будем использовать вектор-столбец ()б), k-й элемент которого равен разности напряжений k-го и балансирующего узлов:

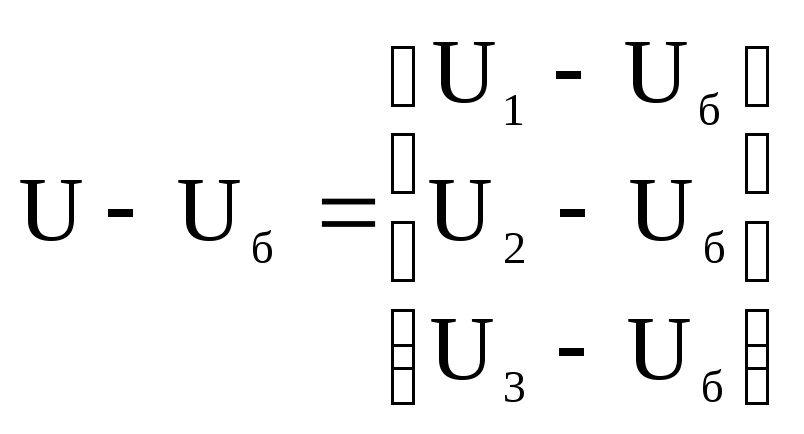. (9.20)

Тогда уравнения узловых напряжений при (9.19) в матричной форме будут иметь вид:

. (9.21)

Выбор балансирующего узла, а также его напряжения (например, или ) не оказывают влияния на результат расчета установившегося режима линейных электрических систем.

Для нелинейных уравнений установившегося режима выбор балансирующего узла и его напряжение оказывают влияние на результат расчета режима. При расчетах установившегося режима электрических систем используются уравнения узловых напряжений (9.21), так как обычно в качестве балансирующего узла применяется станция, ведущая по частоте, напряжение которой, конечно, не равно нулю.

Для сети переменного тока система уравнений узловых напряжений может быть записана в виде комплексной системы:

. (9.22)

где - вектор-столбец, k-й элемент которого равен .

Используя (9.22) можно записать (9.12) в виде системы действительных уравнений порядка 2n следующим образом:

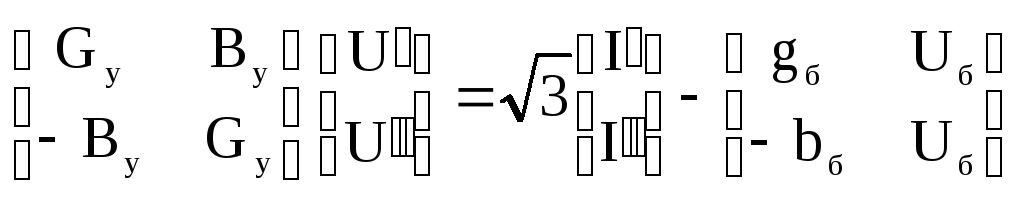. (9.23)

где и - вектор-столбцы;

, - активные и реактивные взаимные проводимости узлов k и б.

9.4. Матрица собственных и взаимных проводимостей узлов

Матрица собственных и взаимных проводимостей узлов играет важную роль в расчетах установившихся режимов электрических систем.

Матрица собственных и взаимных проводимостей симметричная, то есть . Важнейшим свойством матрицы является очень большое количество нулевых элементов. Как отмечалось выше, если узлы не соединены между собой ветвью, то их взаимная проводимость равна нулю. В электрической системе каждый узел связан лишь с небольшим количеством соседних узлов. Пусть, например, в электрической системе из 100 узлов первый узел связан с десятью другими. Тогда в первой строке и в первом столбце матрицы десять ненулевых проводимостей, а остальные девяносто равны нулю. Как правило, большинство узлов в электрических системах соединены со значительно меньшим количеством узлов, чем десять. С учетом симметричности матрицы необходимо запомнить столько ненулевых взаимных проводимостей, сколько ветвей в электрической системе, и столько собственных узловых проводимостей, сколько узлов в системе.

Из сказанного легко убедиться, насколько меньше памяти требуется для запоминания ненулевых элементов матрицы в сравнении с тем случаем, когда пришлось бы запоминать все элементы этой матрицы, число которых равно . Возможность использовать наличие нулевых элементов в матрицах уравнений является важнейшим свойством, которое надо учитывать при сопоставлении различных методов расчетов установившихся режимов.