
лекции / Лекция №8 2-я редакция
.doc8. Лекция №8
8.1. Преобразование сети и исключение узлов
Кратко рассмотрим простейшие эквивалентные преобразования сети [2].
Преобразование
1. Заменить
линии 12, 13, 14 (рис.8.1.) одной эквивалентной
линией Э1 так, чтобы напряжение в узле
1 и ток
![]() ,
текущей из
,
текущей из
у
Рис.8.1.
Замена нескольких линий одной
эквивалентной при
Рис.8.1. Замена
нескольких линий одной эквивалентной
при
![]() ,
,
![]() :
а – три линии,
сходящиеся в узле; б – эквивалентная
линии
:
а – три линии,
сходящиеся в узле; б – эквивалентная
линии![]()
![]()


![]() ,
,
![]() :
а – три линии,
сходящиеся в узле; б – эквивалентная
линии
:
а – три линии,
сходящиеся в узле; б – эквивалентная
линии
![]()
![]() зла
1 в сеть, в преобразованной и непреобразованной
сетях были одинако-
зла
1 в сеть, в преобразованной и непреобразованной
сетях были одинако-
выми. Поставленные условия преобразования сети способствуют требованию неизменной части сети, находящейся за узлом 1.
По эквивалентной линии Э1 должен проходить ток:
![]() , (8.1)
, (8.1)
где
![]() ,
,![]() ,
,![]() - токи по линиям 21, 31, 41.
- токи по линиям 21, 31, 41.
Проводимость
![]() эквивалентной линии Э1 равна сумме
проводимостей линий 21, 31 и 41:
эквивалентной линии Э1 равна сумме
проводимостей линий 21, 31 и 41:
![]() . (8.2)
. (8.2)
Известные фазные
напряжения узлов 2, 3, 4 неодинаковы и
равны
![]() ,
,
![]() и
и
![]() .
Чтобы получить выражение для
эквивалентного напряжения
.
Чтобы получить выражение для
эквивалентного напряжения
![]() узла Э, надо выразить в (8.1) токи в линиях
через узловые напряжения и проводимости
линий следующим образом:
узла Э, надо выразить в (8.1) токи в линиях
через узловые напряжения и проводимости
линий следующим образом:
![]() . (8.3)
. (8.3)
Из выражения (8.3) с учетом (8.2) следует формула для эквивалентного напряжения узла Э:
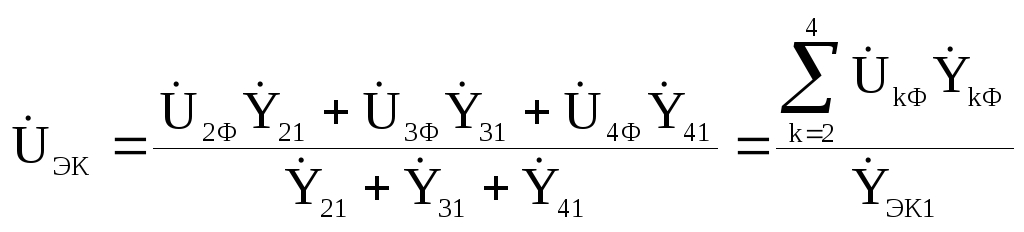 . (8.4)
. (8.4)
При развертывании
сети можно определить токи в линиях 21,
31 и 41 на рис.8.2,а. Для этого в сети на
рис.8.2,б надо найти
![]() ,
а затем найти токи в линиях сети на
рис.8.2,а по закону Ома.
,
а затем найти токи в линиях сети на
рис.8.2,а по закону Ома.
Преобразование линий является эквивалентным только для линейных уравнений установившегося режима.
П
Рис.8.3. Перенос
нагрузок: а –
исходная линия; б – исключение узла 5;
в – исключение узла 3![]()
 реобразование
2. Заменить нагрузку в
узле 5 эквивалентными, расположенными
в узлах 2 и 3 (рис.8.3,а) [2]. Перенос нагрузки
из узла 5 в узлы 2 и 3 соответствует
исключению узла 5. В результате переходим
от сети с пятью узлами (рис.8.3,а) к сети
четырьмя узлами (рис.8.3,б).
реобразование
2. Заменить нагрузку в
узле 5 эквивалентными, расположенными
в узлах 2 и 3 (рис.8.3,а) [2]. Перенос нагрузки
из узла 5 в узлы 2 и 3 соответствует
исключению узла 5. В результате переходим
от сети с пятью узлами (рис.8.3,а) к сети
четырьмя узлами (рис.8.3,б).
Ниже будем говорить о переносе мощностей нагрузок, имея в виду линейные уравнения установившегося режима, для которых справедливо следующее соотношение:
![]() , (8.6)
, (8.6)
где
![]() - номинальное напряжение сети.
- номинальное напряжение сети.
При описании сети нелинейными уравнениями установившегося режима перенос мощностей нагрузок не является эквивалентным преобразованием.
Эквивалентное сопротивление участка 23 на рис.8.3,б:
![]() . (8.7)
. (8.7)
Эквивалентные
нагрузки в узлах 2 и 3 сети на рис.8.3,б
![]() и
и
![]() определяются из условия неизменности
мощностей
определяются из условия неизменности
мощностей
![]() и
и
![]() в линиях 12 и 43 в исходной и преобразованной
сетях.
в линиях 12 и 43 в исходной и преобразованной
сетях.
Если учесть, что
![]() , (8.8)
, (8.8)
то после простых преобразований можно получить следующие выражения для эквивалентных нагрузок:
![]()
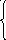 ;
(8.9)
;
(8.9)
![]() . (8.10)
. (8.10)
Из (8.9) и (8.10) видно,
что нагрузки
![]() и
и
![]() в преобразованной сети состоят из двух
слагаемых: нагрузок непреобразованной
сети
в преобразованной сети состоят из двух
слагаемых: нагрузок непреобразованной
сети
![]() и
и
![]() и добавочных перенесенных нагрузок:
и добавочных перенесенных нагрузок:
![]()
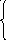 ; (8.11)
; (8.11)
![]() . (8.12)
. (8.12)
Такое определение перенесенных нагрузок справедливо и для случая, когда надо перенести не одну, а две или более нагрузок. Например, можно перенести нагрузки 5 и 3 в узлы 2, 4 на рис.8.3,а. В результате получим сеть, приведенную на рис.8.3,в.
Поскольку разнесение нагрузок не влияет на величину уравнительной мощности, приведенные рассуждения справедливы и в общем случае, когда не равны напряжения в узлах 1 и 4.
С помощью
рассмотренного способа можно разнести
нагрузку
![]() ,
приложенную в центре звезды (рис.8.4), при
соблюдении условия, что падения напряжения
между узлами 1,2 и 3 останутся прежними
и состояние остальной части сети не
изменится.
,
приложенную в центре звезды (рис.8.4), при
соблюдении условия, что падения напряжения
между узлами 1,2 и 3 останутся прежними
и состояние остальной части сети не
изменится.
Рис.8.4. Перенос
нагрузки из центра звезды: а
– исходная линия; б – преобразован-
ная схема
 Преобразование
3. Преобразовать треугольник
сопротивлений в звезду и обратно
(рис.8.5).
Преобразование
3. Преобразовать треугольник
сопротивлений в звезду и обратно
(рис.8.5).
Рис.8.5. Преобразование
звезды в треугольник и обратно: а
– звезда; б – треугольник
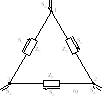 Рассмотрим
преобразования замкнутой сети, приведенной
на рис.8.6,а [2]. Будем считать, что напряжения
узлов питания 1 и 2
Рассмотрим
преобразования замкнутой сети, приведенной
на рис.8.6,а [2]. Будем считать, что напряжения
узлов питания 1 и 2
![]() и
и
![]() равны по модулю и по фазе.
равны по модулю и по фазе.

![]()
![]()


![]()
![]()
![]()
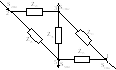
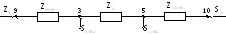 Сначала
разнесем нагрузки
Сначала
разнесем нагрузки
![]() ,
,
![]() ,
,
![]() и перейдем к схеме на рис.8.6,б. Нагрузку
6 разнесем в узлы 2 и 5, нагрузку 7 – в узлы
3 и 5, нагрузку 8 – в узлы 1 и 4. При этом
освобождаются от нагрузок линии 25, 35 и
14. Далее исключим нагрузку
и перейдем к схеме на рис.8.6,б. Нагрузку
6 разнесем в узлы 2 и 5, нагрузку 7 – в узлы
3 и 5, нагрузку 8 – в узлы 1 и 4. При этом
освобождаются от нагрузок линии 25, 35 и
14. Далее исключим нагрузку
![]() ,
которую разнесем в узлы 3 и 1, и перейдем
к схеме на рис.8.6,в. Можно было бы вместо
разнесения нагрузки
,
которую разнесем в узлы 3 и 1, и перейдем
к схеме на рис.8.6,в. Можно было бы вместо
разнесения нагрузки
![]() в узлы 4 и 1, а затем нагрузки
в узлы 4 и 1, а затем нагрузки
![]() в узлы 3 и 1 сразу разнести обе нагрузки
в узлы 3 и 1 сразу разнести обе нагрузки
![]() и
и
![]() в узлы 3 и 1. При этом можно было бы сразу
перейти от рис.8.6,а к рис.8.6,в. При первом
преобразовании сети, то есть при переходе
от рис.8.6,а к рис.8.6,б, получаем следующие
эквивалентные нагрузки в узлах 1 – 5:
в узлы 3 и 1. При этом можно было бы сразу
перейти от рис.8.6,а к рис.8.6,в. При первом
преобразовании сети, то есть при переходе
от рис.8.6,а к рис.8.6,б, получаем следующие
эквивалентные нагрузки в узлах 1 – 5:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
последняя цифра 1 в индексе соответствует
шагу преобразования сети. Эквивалентные
нагрузки определяются по формулам типа
(8.9) и (8.10). На втором шаге преобразования
сети, то есть при переходе к схеме на
рис.8.6,в, нагрузки в узлах 5 и 2 не меняются,
а изменяются только эквивалентные
нагрузки в узлах 1 и 3. Эти нагрузки
,
последняя цифра 1 в индексе соответствует
шагу преобразования сети. Эквивалентные
нагрузки определяются по формулам типа
(8.9) и (8.10). На втором шаге преобразования
сети, то есть при переходе к схеме на
рис.8.6,в, нагрузки в узлах 5 и 2 не меняются,
а изменяются только эквивалентные
нагрузки в узлах 1 и 3. Эти нагрузки
![]() ,
,
![]() определяются по тем же выражениям (8.9)
и (8.10).
определяются по тем же выражениям (8.9)
и (8.10).
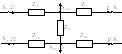
Разрежем сеть на
рис.8.6,в по узлам питания 2 и 1 и перейдем
к сети на рис.8.6,г. Узел питания 1 на
рис.8.6,в разрежем на два узла
![]() и
и
![]() ,
линия
,
линия
![]() на рис.8.6,г совпадает с линией 13 на
рис.10.6,в, то есть
на рис.8.6,г совпадает с линией 13 на
рис.10.6,в, то есть
![]() .
Аналогично
.
Аналогично
![]() .
Таким же образом узел питания 2 на
рис.8.6,в разрежем на два узла питания
.
Таким же образом узел питания 2 на
рис.8.6,в разрежем на два узла питания
![]() и
и
![]() на рис.8.6,г. При этом
на рис.8.6,г. При этом
![]() и
и
![]() .
До сих пор при преобразованиях схем
использовался только разнос нагрузок.
Теперь используем преобразование двух
параллельных линий в одну эквивалентную.
Сложим параллельные линии
.
До сих пор при преобразованиях схем
использовался только разнос нагрузок.
Теперь используем преобразование двух
параллельных линий в одну эквивалентную.
Сложим параллельные линии
![]() и
и
![]() на рис.8.6,г и получим эквивалентную линию
39 на рис.8.6,д. Аналогично сложим параллельные
линии
на рис.8.6,г и получим эквивалентную линию
39 на рис.8.6,д. Аналогично сложим параллельные
линии
![]() и
и
![]() на рис.8.6,г и получим эквивалентную линию
5-10 на рис. 8.6,д. Эквивалентные сопротивления
на рис.8.6,г и получим эквивалентную линию
5-10 на рис. 8.6,д. Эквивалентные сопротивления
![]() и
и
![]() на рис. 8.6,д определяются по обычным
выражениям для определения эквивалентных
сопротивлений при сложении параллельных
линий, например
на рис. 8.6,д определяются по обычным
выражениям для определения эквивалентных
сопротивлений при сложении параллельных
линий, например
![]() . (8.13)
. (8.13)
Последнее выражение эквивалентно (8.13) для случая, когда складываются две параллельные линии. Эквивалентные напряжения узлов 9 и 10 определяются по выражению (8.4).
Таким образом, использование переноса нагрузок и сложения параллельных линий позволило перейти от сложной замкнутой сети на рис.8.6,а к линии с двухсторонним питанием на рис.8.7,д.
8.2. Расчеты однородных сетей, метод расщепления сети
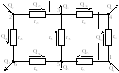
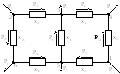
Для однородной сети (рис.8.7,а) можно показать, что система линейных уравнений контурных комплексных мощностей эквивалентна двум системам уравнений, одна из которых содержит только активные мощности в контурах и реактивные сопротивления (рис.8.7,б), а другая – только реактивные мощности и активные сопротивления (рис.8.7,в).
Итак, при расщеплении
сложных однородных сетей, например
приведенной на рис.8.7,а, составляются
две независимые схемы сети: одна – с
р
Рис.8.7. Расщепление
сложных однородных сетей: а
– полная схема сети; б – схема сети с
реактивными сопротивлениями и активными
нагрузками; в – схема сети с активными
сопротивлениями и реактивными нагрузками
Рис.8.8. Неоднородная
сеть разных номинальных напряжений![]()
![]()
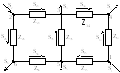
![]() еактивными
сопротивлениями и активными нагрузками
(рис.8.7,б), вторая – с активными
сопротивлениями и реактивными нагрузками
(рис.8.7,в). В каждой из них находится
распределение мощностей; накладывая
друг на друга распределение активных
и реактивных мощностей, найдем
распределение полных мощностей в схеме
на рис.8.7,а. Полная схема замещения при
таком подходе разбивается на две, что
и дало основание для условного названия
«расщепление» сети. Нетрудно убедится,
что объем вычислений для нах
еактивными
сопротивлениями и активными нагрузками
(рис.8.7,б), вторая – с активными
сопротивлениями и реактивными нагрузками
(рис.8.7,в). В каждой из них находится
распределение мощностей; накладывая
друг на друга распределение активных
и реактивных мощностей, найдем
распределение полных мощностей в схеме
на рис.8.7,а. Полная схема замещения при
таком подходе разбивается на две, что
и дало основание для условного названия
«расщепление» сети. Нетрудно убедится,
что объем вычислений для нах

Как правило, ряд линий 35 кВ и ниже сооружается с сечениями проводов, мало отличающихся друг от друга. Такие линии приближаются к однородным. Сети более высокого напряжения, особенно 220 кВ и выше, неоднородны. Даже воздушная линия с проводом одинакового сечения является неоднородной при неодинаковых среднегеометрических расстояниях между проводами на участках сети. Наибольшая неоднородность участков сети наблюдается в замкнутых контурах, образованных сетями разных номинальных напряжений (рис.8.8). Трансформаторы Т1 и Т2 имеют большие реактивные и очень малые активные сопротивления, из-за чего значительно нарушается однородность сети.
