2. Выпуклость: определение, признак выпуклости, точки перегиба.

Дифференцируемая функция называется выпуклой вниз на интервале Х, если ее график расположен не ниже касательной к нему в любой точке интервала Х.

Дифференцируемая функция называется выпуклой вверх на интервале Х, если ее график расположен не выше касательной к нему в любой точке интервала Х.

Выпуклую вверх функцию часто называют выпуклой, а выпуклую вниз – вогнутой.

Посмотрите на чертеж, иллюстрирующий эти определения.

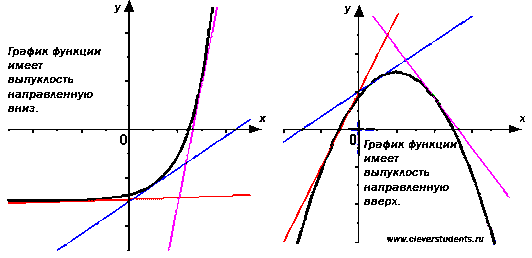
признак выпуклости:

Достаточный признак (выпуклости) вогнутости на интервале :

Пусть функция y = f(x) имеет двойную производную во всех точках

Если <0 во всех точках интервала , то график выпуклый.

Если >0 всюду на интервале , то график вогнутый.

точки перегиба:

Точкой перегиба графика функции называется точка , в которой функция определена и которая разделяет промежутки выпуклости и вогнутости функции. В окрестности такой точки график функции слева и справа от точки имеет разные направления выпуклости. Очевидно, что в точке перегиба касательная пересекает график функции так, что с одной стороны от этой точки график лежит под касательной, а с другой – над нею. В окрестности тоски перегиба график функции геометрически переходит с одной сторон касательной на другую и «перегибается» через неё. Отсюда и произошло название «точка перегиба».

На рисунке ниже представлены несколько примеров точек перегиба (отмечены красными точками). Заметим, что некоторые функции могут не иметь точек перегиба, а другие могут иметь одну, несколько или бесконечно много точек перегиба.

Билет 3

1. Скаляры и векторы.

Скаляр - величина, каждое значение которой может быть выражено одним (действительным) числом без указания направления. Примерами скаляров являются длина, площадь, время, масса, плотность, температура и т. п.

Вектор - это величина, которая характеризуется своим численным значением и направлением.

Вектор как направленный отрезок.

Вектор – это направленный отрезок, то есть такой отрезок, у которого есть начало и конец:

З десь точка А – начало вектора, а точка В – его конец. У вектора есть два параметра: его длина и направление.

Длина вектора – это длина отрезка, соединяющего начало и конец вектора. Длина вектора  обозначается 

Равенство векторов.

Два вектора называются равными, если они сонаправленные и имеют равные модули.

   , т.е, если они совмещаются параллельным переносом (существует такой параллельный перенос, при котором начало и конец одного вектора совмещается с началом и концом другого вектора соответственно).

Операция умножения вектора на число и её свойства.

Произведением вектора на число называется вектор, модуль которого равен произведению модуля вектора на модуль числа, а направление совпадает с направлением умножаемого вектора, если число больше нуля, и противоположно ему, если число меньше нуля. (Если совсем просто, то это вектор в n раз длиннее данного, где n - данное число). Если произвольный вектор умножить на ноль, то получим нулевой вектор. Произведение нулевого вектора и произвольного числа есть нулевой вектор

Свойства операций умножения вектора на число:

1. Сочетательное свойство умножения

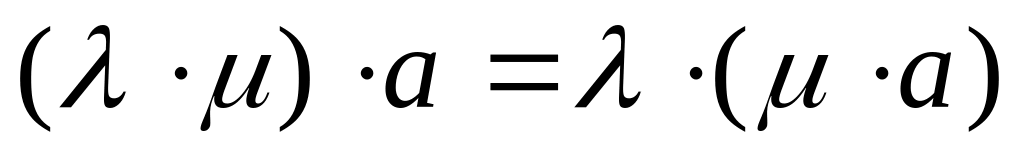
2. Первое распределительное свойство

3. Второе распределительное свойство .

4. Нейтральным числом по умножению является единица, то есть .

При умножении вектора на единицу с ним не производится никаких геометрических преобразований.

5. 

6. 

Здесь и - произвольные векторы, а и - произвольные числа.

Коллинеарные векторы.

Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.

Выражение коллинеарных векторов друг через друга.

Пусть ,и пусть модуль вектора в раз превышает модуль вектора , т. е. .

Тогда .Таким образом, в векторе укладывается векторов .

Пусть теперь и . Тогда .

Сумма векторов и её свойства.

Суммой векторов с координатами a₁, a₂  и с координатами b₁, b₂ называется такой третий вектор с координатами а1 + b1, a2 + b2. Начало этого вектора совпадает с началом вектора , а конец – с концом вектора при условии, что начало вектора совпадает с концом вектора (правило треугольников)

А при совмещенных началах этих трех векторов, векторы и служат сторонами параллелограмма, а вектор c -- его диагональю .         (правило параллелограмма)

Свойства суммы векторов:

1°    - коммутативность

2°    - ассоциативность

3°   

4°   

Противоположный вектор.

Два вектора называются противоположными, если они противоположно направлены и их длины равны.

Разность векторов.

Разностью векторов и с координатами и называется вектор с координатами , т.е. это такой вектор , который в сумме с вектором даст вектор.