Билет 1

1. Система двух линейных уравнений с двумя неизвестными. Совместные и несовместные системы. Матрицы коэффициентов системы. Определители 2-го порядка. Вывод формулы Крамера решения системы второго порядка. Геометрическая интерпретация системы и её решения.

2. Асимптоты: вертикальные и наклонные.

Билет 2

1. Минор, дополнительный к выделенному элементу матрицы. Алгебраическое дополнение к выделенному элементу матрицы. Вычисление определителя 3-го порядка разложением по элементам строки или столбца. Решение системы линейных уравнений 3-го порядка по правилу Крамера.

2. Выпуклость: определение, признак выпуклости, точки перегиба.

Билет 3

1. Скаляры и векторы. Вектор как направленный отрезок. Равенство векторов. Операция умножения вектора на число и её свойства. Коллинеарные векторы. Выражение коллинеарных векторов друг через друга. Сумма векторов и её свойства. Противоположный вектор. Разность векторов.

2. Экстремумы: определение, необходимое условие, достаточные условия.

Билет 4

1. Линейная комбинация векторов. Разложение вектора на плоскости по двум неколлинеарным векторам. Компланарные векторы. Разложение вектора по трем некомпланарным векторам. Линейная зависимость и линейная независимость системы векторов.

2. Формула Лангранжа (формула конечных приращений) и её геометрическая интерпритация. Признаки монотонности функций.

Билет 5

1. Базис. Ортогональный базис. Ортонормированный базис. Декартовая прямоугольная система координат. Левая и правая системы координат. Координаты вектора – коэффициенты его разложения в ортогональном базисе. Коэффициенты разложения – проекции на оси координат. Радиус – вектор точки. Длина вектора «в координатах». Направление вектора. «Направляющие» косинусы и зависимость между ними.

2. Формула Лангража конечных приращений. Правило Лопиталя (вывод). Примеры его применения.

Билет 6

1. Скалярное произведение векторов. Его физический смысл. Свойства скалярного произведения. Доказать равенство a(b+c)=ab+ac. Вычисление скалярного произведения через координаты (вывод). Условие перпендикулярности двух векторов в векторной и координатной формах.

2. Дифференциал: определение, геометрическая интерпретация, применение к приближенным вычислениям. Инвариантность формы дифференциала.

Билет 7

1. Векторное произведение двух векторов и его физический смысл. Свойства векторного произведения. Вычисление векторного произведения «в координатах» (с выводом).

2. Нахождение производной функции, заданной параметрически (с обоснованием). Нахождение производной функции, заданной неявно (на примере).

Билет 8

1. Смешанное произведение векторов. Его геометрический смысл. Вычисление смешанного произведения через координаты векторов (вывод).

2. Производная сложной функции, производная обратной функции (с доказательствами).

Билет 9

1. Вывод общего уравнения прямой на плоскости. Вывести уравнение прямой на плоскости с угловым коэффициентом и уравнение прямой в отрезках на осях. Вывести канонические уравнения прямой на плоскости, записать параметрические уравнения, вывести уравнение прямой, проходящей через две заданные точки.

2. Правила дифференцирования: доказать формулу , перечислить остальные.

Билет 10

1. Угол между прямыми на плоскости, если они заданы каноническими уравнениями или уравнениями с угловым коэффициентом (вывод). Вывести условия параллельности, совпадения и перпендикулярности прямых на плоскости.

2. Производная: физические задачи, приводящие к понятию производной, определение. Геометрическая интерпретация (уравнения касательной и нормали).

Билет 11

1. Вывести формулу для вычисления расстояния от точки до прямой на плоскости.

2. Доказательство первого замечательного предела .

Билет 12

1. Вывести общее уравнение плоскости. Получить уравнение плоскости в отрезках и уравнение плоскости, проходящей через три заданные точки (с выводом).

2. Предел функции: определение свойства. Непрерывность: определение, односторонние пределы и виды разрывов (с примерами).

Билет 13

1. Вывести формулу для вычисления расстояния от точки до плоскости. Как вычисляется угол между плоскостями? Вывести условия параллельности и перпендикулярности двух плоскостей.

2. Функция: определение, способы задания, четность, периодичность, обратная функция. Графики функций: , , , .

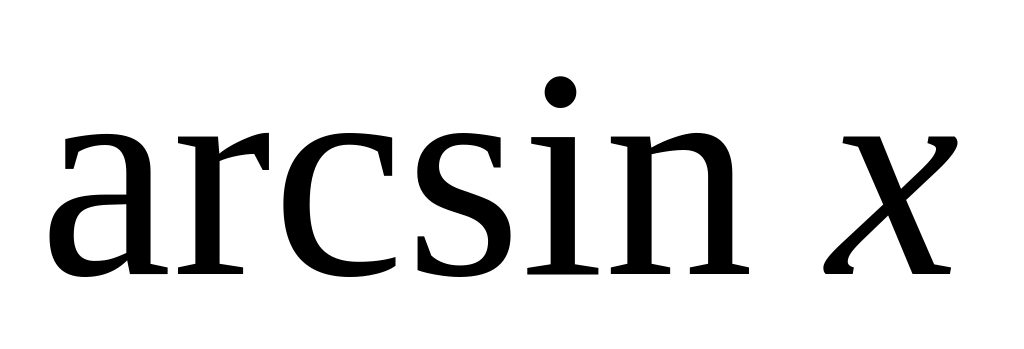Билет 14

1. Записать векторное уравнение прямой в пространстве, получить канонический вид уравнений прямой в пространстве. Вывести параметрические уравнения прямой в пространстве, а также прямой, проходящей через две точки пространства. Как определяется угол между двумя прямыми в пространстве (вывод)? Записать условия параллельности и перпендикулярности прямых в пространстве.

2. Последовательности: определение, предел, свойства сходящихся последовательностей.

Билет 15 (2-ой вопрос как 2- ой вопрос билета 13 )

1. Как определяется угол между прямой и плоскостью? Записать условия перпендикулярности, параллельности прямой и плоскости. Вычисление координат точки пересечения прямой и плоскости.

2. Функция: определение, способы задания, четность, периодичность, обратная функция. Графики функций: , , , .

Билет 16 (полностью как билет 1)

1. Система двух линейных уравнений с двумя неизвестными. Совместные и несовместные системы. Матрицы коэффициентов системы. Определители 2-го порядка. Вывод формулы Крамера решения системы второго порядка. Геометрическая интерпритация системы и её решения.

2. Асимптоты: вертикальные и наклонные.

Билет 17 (полностью как билет 2)

1. Минор, дополнительный к выделенному элементу матрицы. Алгебраическое дополнение к выделенному элементу матрицы. Вычисление определителя 3-го порядка разложением по элементам строки и столбца. Решение системы линейных уравнений 3-го порядка по правилу Крамера.

2. Выпуклость: определение, признак выпуклости, точки перегиба.

Билет 18 (полностью как билет 3)

1. Скаляры и векторы. Вектор как направленный отрезок. Равенство векторов. Операция умножения вектора на число и её свойства. Коллинеарные векторы. Выражение коллинеарных векторов друг через друга. Сумма векторов и её свойства. Противоположный вектор. Разность векторов.

2. Экстремумы: определение, необходимое условие, достаточные условия.

Билет 19 (полностью как билет 4)

1. Линейная комбинация векторов. Разложение вектора на плоскости по двум неколлинеарным векторам. Компланарные векторы. Разложение вектора по трем некомпланарным векторам. Линейная зависимость и линейная независимость системы векторов.

2. Формула Лангража. (формула конечных приращений) и её геометрическая интерпретация. Признаки монотонности функций.

Билет 20 (полностью как билет 5)

1. Базис. Ортогональный базис. Ортонормированный базис. Декартовая прямоугольная система координат. Левая и правая система координат. Координаты вектора – коэффициенты его разложения в ортогональном базисе. Коэффициенты разложения – проекции на оси координат. Радиус – вектор точки. Длина вектора «в координатах». Направление вектора. «Направляющие» косинусы и зависимость между ними.

2. Формула Лангража конечных приращений. Правило Лопиталя (вывод). Примеры его применения.

Билет 21 (полностью как билет 6)

1. Скалярное произведение векторов. Его физический смысл. Свойства скалярного произведения. Доказать равенство a(b+c)=ab+ac. Вычисление скалярного произведения через координаты (вывод). Условие перпендикулярности двух векторов в векторной и координатной формах.

2. Дифференциал: определение, геометрическая интерпретация, применение к приближенным вычислениям. Инвариантность формы дифференциала.

Билет 22 (полностью как билет 7)

1. Векторное произведение двух векторов и его физический смысл. Свойства векторного произведения. Вычисление векторного произведения «в координатах» (вывод).

2. Нахождение производной функции, заданной параметрически (с обоснованием). Нахождение производной функции, заданной неявно (на примере).

Билет 23 (полностью как билет 8)

1. Смешанное произведение векторов. Его геометрический смысл. Вычисление смешанного произведения через координаты векторов (вывод).

2. Производная сложной функции (с доказательством). Производная обратной функции (вывод).

Билет 24 (полностью как билет 9)

1. Вывод общего уравнения прямой на плоскости. Вывести уравнение прямой на плоскости с угловым коэффициентом и уравнение прямой в отрезках на осях. Вывести канонические уравнения прямой на плоскости, записать параметрические уравнения, вывести уравнение прямой, проходящей через две заданные точки.

2. Правила дифференцирования: доказать формулу . Перечислить остальные.

Билет 25 (полностью как билет 10)

1. Угол между прямыми на плоскости, если они заданы каноническими уравнениями или уравнениями с угловым коэффициентом (вывод). Вывести условия параллельности, совпадения и перпендикулярности прямых на плоскости.

2. Производная: физические задачи, приводящие к понятию производной, определение, геометрическая интерпретация (уравнение касательной и нормали).

Билет 26 (полностью как билет 11)

1. Вывести формулу для вычисления расстояния от точки до прямой на плоскости.

2. Доказательство первого замечательного предела .

Билет 27 (полностью как билет 12)

1. Вывести общее уравнение плоскости. Получить уравнение плоскости в отрезках и уравнение плоскости, проходящей через три заданные точки (с выводом).

2. Непрерывность: определение, односторонние пределы и виды разрывов (с примерами).

Билет 28 (1-ый вопрос как 1-ый 13-го билета, 2-ой как 2-ой 12-го билета

1. Вывести формулу для вычисления расстояния от точки до плоскости. Как вычисляется угол между плоскостями? Вывести условия параллельности и перпендикулярности двух плоскостей.

2. Предел функции: определение, свойства. Непрерывность: определение, односторонние пределы и виды разрывов (с примерами).

Билет 29 (как билет 14)

1. Записать векторное уравнение прямой в пространстве, получить канонический вид уравнений прямой в пространстве. Вывести параметрические уравнения прямой в пространстве, а также прямой, проходящей через две точки пространства. Угол между двумя прямыми в пространстве (вывод). Записать условия параллельности и перпендикулярности прямых в пространстве.

2. Последовательности: определение, предел, свойства сходящихся последовательностей.

Билет 30 (полностью как билет 15, 2-ой вопрос и как у билета 13)

1. Как определяется угол между прямой и плоскостью? Записать условия перпендикулярности, параллельности прямой и плоскости. Вычисление координат точки пересечения прямой и плоскости.

2. Функция: определение, способы задания, четность, периодичность, обратная функция. Графики функции: sin x, arcsin x, e в степени x, ln x.

ОТВЕТЫ

Билет 1

1. Система двух линейных уравнений с двумя неизвестными.

Системой двух линейных уравнений с двумя неизвестными называется совокупность уравнений вида:

,где х и у — неизвестные величины, а и — некоторые заданные числа.

Совместные и несовместные системы.

Система уравнений, имеющая хотя бы одно решение, называется совместной, а не имеющая ни одного решения — несовместной.

Матрицы коэффициентов системы.

Cистему из уравнений с неизвестными

можно представить в матричном виде

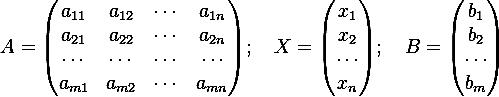
и тогда всю систему можно записать так:

, где имеет смысл таблицы коэффициентов cистемы уравнений.

Определители 2-го порядка.

Определителем второго порядка называется число равное разности произведений элементов главной и второй диагонали:

Примеры определителей второго порядка:

Вывод формулы Крамера решения системы второго порядка.

Рассмотрим систему 2-х уравнений с двумя неизвестными

Используя определители 2-го порядка, решение такой системы можно записать по правилу Крамера в следующем виде: если D¹0. Здесь .

вывод формул.

Пусть нам требуется решить систему линейных уравнений вида где x₁, x₂ – неизвестные переменные, a_{i j}, i = 1, 2, j = 1, 2 – числовые коэффициенты, b₁, b₂ - свободные члены. Решением СЛАУ называется такой набор значений x₁, x₂ при которых оба уравнения системы обращаются в тождества.

В матричном виде эта система может быть записана как A ⋅ X = B, где - основная матрица системы, ее элементами являются коэффициенты при неизвестных переменных, - матрица – столбец свободных членов, а - матрица – столбец неизвестных переменных. После нахождения неизвестных переменных x₁, x₂ матрица становится решением системы уравнений и равенство A ⋅ X = B обращается в тождество .

Будем считать, что матрица А – невырожденная, то есть, ее определитель отличен от нуля. В этом случае система линейных алгебраических уравнений имеет единственное решение, которое может быть найдено методом Крамера.

Метод Крамера основывается на двух свойствах определителя матрицы:

1. Определитель квадратной матрицы , 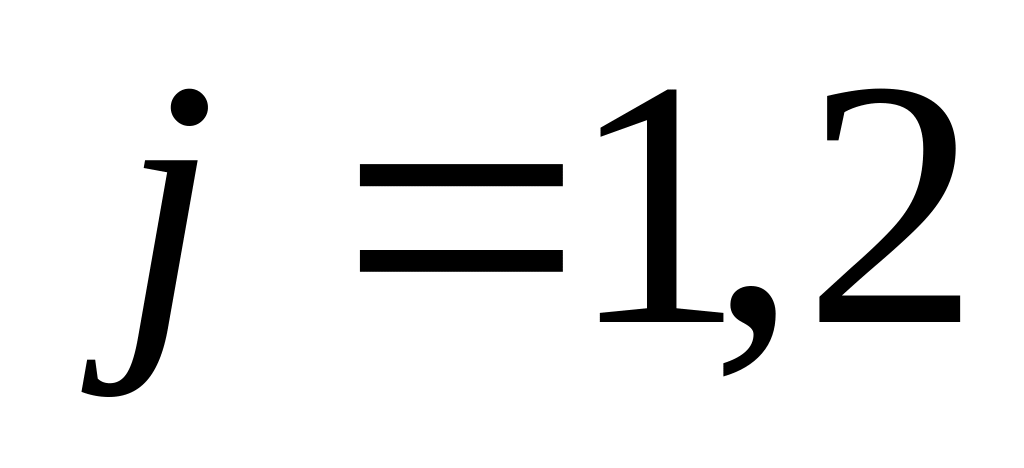равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения:

Сумма произведений элементов какой-либо строки (столбца) квадратной матрицы на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю:

Итак, приступим к нахождению неизвестной переменной x₁. Для этого умножим обе части первого уравнения системы на А₁₁, обе части второго уравнения – на А_{2 1} (то есть, уравнения системы умножаем на соответствующие алгебраические дополнения первого столбца матрицы А):

Сложим все левые части уравнения системы, сгруппировав слагаемые при неизвестных переменных x₁, x₂, и приравняем эту сумму к сумме всех правых частей уравнений:

Если обратиться к озвученным ранее свойствам определителя, то имеем и предыдущее равенство примет вид откуда

Аналогично находим x₂. Для этого умножаем обе части уравнений системы на алгебраические дополнения второго столбца матрицы А:

Складываем все уравнения системы, группируем слагаемые при неизвестных переменных x₁, x₂ и применяем свойства определителя:

Откуда .

Если обозначить . то получаем формулы для нахождения неизвестных переменных по методу Крамера

, .

Пример Решить систему линейных уравнений при помощи правила Крамера:

Решение. Находим определитель основной матрицы системы

Поскольку D¹0, то для нахождения решения системы можно применить правило Крамера, но предварительно вычислим еще два определителя:

,

Тогда

Проверка:

Следовательно, решение найдено правильно.

Геометрическая интерпретация системы и её решения.

Как известно, уравнения с двумя переменными вида

Описывают на координатной плоскости Оху прямую. Система двух уравнений такого вида означает, что ее решения как точки на координатной плоскости должны принадлежать одновременно двум прямым, соответствующим уравнениям этой системы.

Отсюда возможны следующие варианты:

а) обе прямые пересекаются, и тогда система имеет единственное решение;

б) прямые параллельны, и система не имеет решения (несовместна);

в) прямые совпадают, т. е. ранг системы равен единице, и система имеет бесчисленное множество решений.