
Лекции / Лекция 21 Характеристики и диаграммы СГ
.pdfХарактеристики и диаграммы синхронных генераторов
Характеристики синхронных генераторов. Основными ха-
рактеристиками синхронного генератора, работающего на автономную нагрузку, являются: характеристика холостого хода, характеристика короткого замыкания, нагрузочная, внешняя и регулировочная. Первые три используются для определения индуктивных сопротивлений генератора и других параметров.
Характеристика холостого хода. Характеристика холостого хо-
да представляет зависимость E f (If ) при постоянной частоте враще-
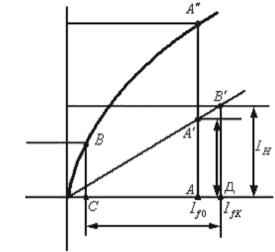
ния. Она снимается в восходящей и нисходящей ветвях. Площадь, ограниченная этими кривыми, определяется величиной гистерезиса магнитной цепи ротора. Для построения диаграмм напряжения и других характеристикрекомендуется использовать нисходящую ветвь с нулем, помещенным в точке пересечения кривой с осью абсцисс. При изменении тока возбуждения от нуля ЭДС и поток сначала изменяются по линейному закону, а затем из-за насыщения магнитной цепи характеристика холостого хода отклоняется от линейного закона. Чтобы обеспечить лучшее использование материалов, при проектировании рабочая точка выбирается на колене кривой (точка A на рис. 4.1.)
Характеристики холостого хода стандартизированы. В табл. 4.1 даны стандартные характеристики холостого хода для турбо-и гидрогенераторов в относительных единицах. Стандартизация характеристики холостого хода необходима для обеспечения успешного включения генераторов на параллельную работу.
E
Uн
Iн
Iко
Iн Х
0 |
Kid Iн |
If |
Рис. 4.1.Характеристика холостого хода
При холостом ходе, кроме потока в воздушном зазоре, который наводит ЭДС в обмотке статора, есть поток рассеяния обмотки возбуждения, сцепленный только с обмоткой возбуждения. Он замыкается вокруг обмотки возбуждения в межполюсном пространстве. В турбогенераторах он равен 4 – 8% рабочего потока.
Стандартные характеристики холостого хода.
Таблица 4.1.
I f |
|
0.5 |
1 |
1.5 |
2 |
2.5 |
3 |
3.5 |
E |
ТГ |
0.58 |
1 |
1.21 |
1.33 |
1.4 |
1.46 |
1.51 |
|
ГГ |
0.53 |
1 |
1.23 |
1.3 |
1.4 |
1.46 |
1.51 |
Примечание. Т-турбогенератор, Г-гидрогенератор
Характеристика трехфазного короткого замыкания. Эта характе-
ристика снимается при замыкании зажимов всех фаз обмотки статора накоротко и определяет зависимость I f (If ) при U 0 и f1 fн.
Если пренебречь активным сопротивлением обмотки статора, то сопротивление обмотки статора будет чисто индуктивным. Поэтому
угол между ЭДС и током 90 , Iq 0, Id I и

E jIXd .
При коротком замыкании реакция якоря является чисто размагничивающей, ЭДС E от результирующего потока воздушного зазора, равная
E E IXad IX ,
весьма мала, вследствие чего и поток мал. Поэтому при коротком замыкании магнитная цепь не насыщена, характеристика I f (I f )
прямолинейна.
Если известен коэффициент Kid , можно определить МДС реак-
ции якоря в масштабе тока возбуждения Kid IH . Определив по харак-
теристике короткого замыкания величину тока возбуждения при токе к.з., равному номинальному (отрезок ОА на рис. 4.1) и вычтя из него составляющую СД, которая компенсирует чисто продольную размагничивающую реакцию якоря, получим величину тока возбуждения, которая идет на создание ЭДС рассеяния (отрезок ОС). Отрезок ВС соответствует ЭДС E . Отсюда следует
X E .
Iн
Если снимать характеристики короткого замыкания при переменной частоте вращения, то ток короткого замыкания практически не будет зависеть от частоты вращения, т.к. индуктивные сопротивления и ЭДС, индуктированная потоком возбуждения, изменяется пропорционально частоте, следовательно пропорционально частоте вращения.
Только при очень малых частотах, когда становится заметным влияние активного сопротивления ra на величину d , характеристика
Iк f (n) дает перегиб, спускаясь при n 0 к значению Iк 0 .
Отношение короткого замыкания. Отношением короткого за-
мыкания называется отношение тока короткого замыкания Iко при токе возбуждения, соответствующем номинальному напряжению E0 Uн по характеристики холостого хода, к номинальному току статора Iн .
Кокз Iко .
Iн
В соответствии с рис. 4.1
Iко Uн .
Xd
На основании последних выражений
Kокз XUd нIн *1 .
Xd
Чем больше Кокз , тем больше предельная нагрузка. У гидрогене-
раторов обычно Кокз 0.8 1.8, а турбогенераторов Кокз 0.4 1.0.
Величина Кокз тем больше, чем больше зазор между статором и рото-
ром.
Внешние характеристики. Внешние характеристики определяют зависимость U f (I) при If Const, f Const,Cos Const .
При индуктивной на-
π
грузке 0 реакция якоря и
2
падение напряжения
Ira jIX
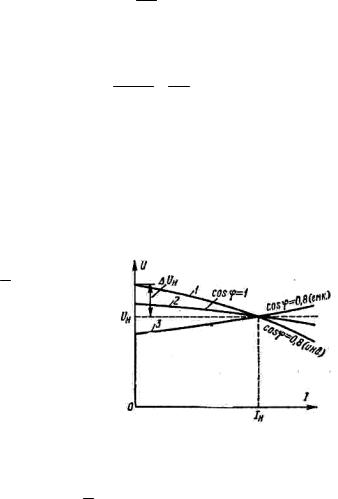
вызывает уменьшение напряжения, поэтому внешняя характеристика имеет резко падающий характер (рис. 4.2), причем с уменьшением величины Cos возрастает вели-
чина падения напряжения. При
Рис. 4.2. Внешние характеристики синхронных генераторов
π
емкостной нагрузке 0 указанные выше факторы действуют в
2
сторону повышения напряжения, поэтому с уменьшением Cos уве-
личивается возрастание напряжения. При U 0 (короткое замыкание) все характеристики пересекаются в одной точке.
Регулировочные характеристики. Регулировочная характери-
стика дает зависимость

If f (I) при
U Const, f Const и
Cos Const . Она показывает, как нужно регулировать ток возбуждения, чтобы при изменении нагрузки его напряжение оставалось постоянным. Для различных значений Cos регу-
лировочные характеристики показаны на рис. 4.3.
Вид характеристик также объясняется характером действия реакции
якоря. При отстающем токе продольная составляющая реакции якоря является размагничивающей и для компенсации ее влияния с увеличением I необходимо значительно увеличивать ток возбуждения. При чисто активной нагрузке продольная размагничивающая реакция якоря слабее и требуется меньшее увеличение If . При опережающем токе
продольная реакция якоря стремится увеличить напряжение, вследствие чего с увеличением тока I необходимо уменьшать If .
Нагрузочные характеристики. Эта характеристика определяет зависимость U f (If ) при I Const, Cos Const, f Const и пока-
зывает, как изменяется напряжение генератора U с изменением тока возбуждения If при условии постоянства I и Cos . Наибольший
интерес представляет так называемая индукционная нагрузочная характеристика (рис. 4.3), которая соответствует чисто индуктивной нагрузке генератора, когда Cos 0 . Обычно она снимается при Iн .
Нагрузочные характеристики при Сos 0.8 ( 0) и Cos 1 прохо-
дят выше характеристики при Cos 0 и не являются параллельными по отношению к характеристике холостого хода E0 f (If ) . Характе-
ристики при Сos 0.8 и Cos 0 при 0 проходят выше характеристики холостого хода.

|
На рис. 4.4 треугольник СBA называется реактивным. Катет CB |
||||||||
равен |
падению |
напряже- |
|
||||||
ния в сопротивлении рас- |
|
||||||||
сеяния |
обмотки статора |
|
|||||||
Iн X , |
катет |
CA |
равен |
|
|||||
МДС |
реакции |
якоря |
в |
|
|||||
масштабе |
тока |
возбужде- |
|
||||||
ния |
Kid Iн . |
Если извест- |
|
||||||
ны: |
1) |
ток |
возбуждения |
|
|||||
Ifк ОА при трехфазном |
|
||||||||
коротком |
замыкании |
и |
|
||||||
I Iн , |
2) Сопротивление |
|
|||||||
X |
и 3) начальная прямо- |
Рис. 4.4. Индукционная нагрузочная |
|||||||
линейная |
часть |
х.х.х., то |
характеристика и реактивный треугольник |
||||||
синхронного генератора |
|||||||||
можно |
|
построить |
тре- |
||||||
|
|
||||||||
угольник |
СBA. |
Составляющая ОС тока возбуждения при коротком |
|||||||
замыкании ОА индуктирует ЭДС E Iн X , а другая составляющая этого тока СА компенсирует размагничивающее действие реакции якоря, и поэтому CA Kid Iн.
МДС реакции якоря и ЭДС рассеяния E Iн X в режиме ин-
дукционной характеристики постоянны, т.к. X при I Const прак-
тически не зависит от величины результирующего потока в зазоре. Поэтому индукционную характеристику 2 можно построить с помощью х.х.х. и реактивного треугольника СBA, передвигая его параллельно самому себе так, чтобы его вершина В скользила по х.х.х. Тогда вершина A опишет характеристику 2. Одно из положений этого тре-
|
|
|
|
при U Uн ) показано на рис. 4.4. |
угольника ( C В А |
|
|||
Согласно кривой 2 на рис. 4.4, для получения Uн КА при |
||||
I Iн и Cos 0 |
( 0) необходим ток возбуждения ОК. Составляю- |
|||
|
|
CA этого тока компенсирует чисто продольную раз- |
||
щая DK C A |
|
|||
магничивающую реакцию якоря в этом режиме, а составляющая OD=OK–DK должна индуцировать результирующую ЭДС величиной
E U IX DC C B DB .
Из х.х.х. на рис. 4.4 следует, что ток OD действительно индуцирует такую ЭДС. Если X и Kid неизвестны, то с помощью характеристик 1

и 2 можно определить X и величину МДС реакции якоря. Так как в по-
следнем случае известны сторона OA O A и угол AOB A O B , то, отложив из некоторой точки A отрезок O A OA и проведя линии O B параллельную ОВ, найдем точку пересечения B с кривой 1. Опустив из точки B вертикаль B C , получим
B C
X Iн ,
а отрезок С А определяет величину МДС реакции якоря в масштабе
If .
Опыт показывает, что опытная индукционная нагрузочная характеристика отклоняется вправо от характеристики, построенной с помощью х.х.х. и реактивного треугольника, тем больше, чем больше напряжение U . Причина этого заключается в том, что хотя для точек B и A величины ЭДС E и потока Ф одинаковы, соответствую-
щие токи возбуждения OD и OK неодинаковы. Так как ОК OD, то поток рассеяния обмотки возбуждения больше, что вызывает увеличение насыщения полюсов и ярма индуктора.
|
Вследствие изложенного при указанном выше методе определе- |
|||||||||
ния |
X вместо отрезка |
A C CA откладывается такой же длины от- |
||||||||
|
|
|
|
|
|
|
|
|
|
. Поэтому вместо |
резок A C |
|
CA и находится отрезок C B |
|
C B |
|
|||||
X |
получим сопротивление |
|
|
|
|
|||||
|
|
|
|
Xp |
C B |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Iн |
|
|
|
|
|
которое называется индуктивным сопротивлением Потье или расчетным индуктивным сопротивлением рассеяния обмотки якоря.
У неявнополюсных машин Xp (1.05 1.1)X , а у явнополюс-
ных Xp (1.1 1.3)X .
Векторные диаграммы напряжений синхронного генерато-
ра. Напряжение фазы обмотки генератора равно сумме индуцируемых в этой обмотке ЭДС минус падение напряжения в активном сопротив-
лении обмотки якоря (статора) ra . В соответствии с этим уравнение напряжения явнополюсного синхронного генератора будет иметь вид:
. . . |
. |
. |
. |
(4.1) |
U E Ead Eaq E I ra . . |
||||
ЭДС реакции якоря и рассеяния в (4.1) выразим через соответствующие токи и индуктивные сопротивления:
. . . . . .
Ead jId Xad; Eaq jIq Xaq; E j I X .
При этом уравнение напряжения примет вид:
. . |
. |
. |
. |
. |
|
|
|
(4.2) |
|
|
|
|
|
||||
U E jId Xad jIq Xaq jI X I ra E jIX jIra |
||||||||
Сопротивления Xad и Xaq можно объединить с сопротивлени-
ем X в синхронные сопротивления:
Xd Xad X ; Xq Xaq X .
Тогда вместо уравнения (4.2) получим:
. |
. |
. |
. |
. |
U E jId Xd jIq Xq I ra.
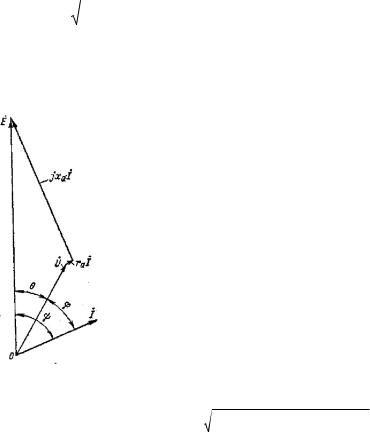
Уравнениям (4.2) на рис. 4.5 соответствует векторная диаграмма явнополюсного синхронного генератора при активно индуктивной нагрузке, когда 0 .
При этом диаграмму на рис. 4.5 можно несколько видоизменить, как показано на рис. 4.6. На этой диаграмме направления векторов падений напряжений изменены на обратные. Поэтому диаграмма соответствует уравнению напряжения вида:

Рис. 4.5. Векторная диаграмма напряжений |
|
Рис.4.6. Видоизмененная диарамма |
||
явнополюсного синхронного генератора |
|
явнополюсного синхронногогенератора |
||
. |
. |
. |
. |
. |
E U I ra jIq Xq jId Xd .
Если из точек A на рис. 4.5 и 4.6 провести перпендикулярно вектору
. |
. |
I отрезки прямых до пересечения в точке Q c вектором |
E , то длины |
. |
. |
этих отрезков на рис. 4.5 будут равны I Xaq , а на рис. 4.6 равны I Xq .
Это следует из того, что в прямоугольных треугольниках АQВ угол при вершине A равен , и поэтому для рис. 4.5
|
AB |
|
. |
|
. |
|
. |
|
|
|
|
Eaq |
|
Iq Xaq |
|
ICos Xaq |
. |
||
AQ |
|
|
|
|
|
|
|
I Xaq , |
|
Cos |
Cos |
Cos |
Cos |
||||||
а для рис. 4.6 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
AQ |
AB |
|
Eq |
|
IqXq |
|
ICos Xq |
IXq . |
|
Cos |
Cos |
Cos |
Cos |
||||||
|
|
|
|
|
|||||
Интересно, что BQ Id Xq |
, а QE (Xd Xq )Id . |
||||||||
Если режим работы синхронного явнополюсного генератора задан величинами U,I, можно найти ЭДС по формуле:
U2 IU(Xd |
Xq )Sin 2UIrCos I2 |
(r Xd Xq ) |
||||
E |
|
|
|
|
|
|
|
|
|
|
|
||
U 2 2UI(Xq Sin rCos ) I2 (r2 |
Xq )2 |
|||||
|
||||||
У неявнополюсного синхронного генератора сопротивления по про-
дольной и поперечной осям равны между собой Xq Xq . Векторная диаграмма для него представлена на рис. 4.7.
|
В синхронных генераторах активным |
|
сопротивлением обмотки статора можно пре- |
|
небречь (r 0) . При этом векторные диа- |
|
граммы упрощаются, что облегчает их ис- |
|
пользование в практических расчётах. На рис. |
|
4.8 и 4.9 показаны векторные диаграммы не- |
|
явнополюсного и явнополюсного синхронно- |
|
го генератора при r 0. Они позволяют по- |
|
лучить более простые формулы для расчёта |
|
ЭДС, если известны U,I, . На рис. 4.8 про- |
|
должим линию БС до пересечения с вектором |
|
тока в точке Д, а линию БС перенесём парал- |
|
лельно самой себе в точку 0. При этом будем |
|
иметь А0=IXq . |
|
Из треугольника ОСД имеем СД= |
Рис.4.7.Векторнаядиа- |
U sin , а из прямоугольного треугольника |
грамма неявнополюсного |
ОБД найдём ЭДС Е: |
синхронного генератора |
|
E
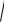 (U cos )2 (Usin IXq)2.
(U cos )2 (Usin IXq)2.
Сдругой стороны по теореме косинусов
