
Лекции / Лекция 06 Трехфазные трансформаторы
.pdf
Трехфазные трансформаторы
Классификация магнитных систем трехфазных трансфор-
маторов. В зависимости от устройства сердечника трехфазного трансформатора различают: а) трансформаторы со связанными магнитными системами и б) трансформаторы с независимыми или почти независимыми магнитными системами.
На рис. 5.1 показан трехстержневой трансформатор со связанной магнитной системой. Характерной особенностью трансформатора на рис. 5.1 является несимметричность его магнитной системы, так как длины магнитных цепей в стержнях A , B и C не равны: длина магнитной цепи в среднем стержне B меньше, чем длины цепей в крайних стержнях A и C . Все три цепи сходятся в узлах О1 и О2 . Если
A , B и C – амплитуды магнитных потоков в стержнях A , B и
C , то, согласно первому закону Киргхгофа в применении к магнитным цепям, имеем в каждом из узлов:
|
|
|
0 |
(5.1) |
A |
В |
С |
|
Рис. 5.1. Магнитная система |
Рис. 5.2. Диаграмма токов |
|
холостого хода трехстержневого |
|
трехстержневого трансформатора |
трансформатора |
|
Будем считать, что трансформатор является простейшим (r1 0, |
||
x1 0, |
pc 0 ) и что к нему подводится синусоидальное симметрич- |
|
ное напряжение. В этом случае напряжения UA , UB и UC и потоки
A B и ФC образуют правильные трехлучевые звезды, причем ка-
ждый вектор потока отстает от соответствующего вектора напряжения на угол 90° (рис. 5.2).
При прохождении потока A по участку O1abO2 (рис. 5.1) воз-
никает падение магнитного потенциала A (Rст+2Rя), где Rст – маг-
нитное сопротивление стержня и Rя – магнитное сопротивление каждой половины верхнего или нижнего ярма. Соответственно для стерж-
ня С имеем С (Rст+2Rя). В стержне В падение магнитного потен-
. . .
циала равно ФB Rст. Если F A , FB и FC – амплитуды МДС, соответ-
ствующие потокам A ,ФB и ФC , то по второму закону Кирхгофа в
применении к магнитным цепям имеем: Для цепи abO2O1
|
|
. |
. |
. |
|
(Rст |
2Rя ) ФB Rст |
FA FB; |
|||
A |
|||||
Для цепи cdO2O1
. . . .
ФC (Rст 2Rя ) ФB Rст FC FB;
Кроме того, в системах без нулевого провода геометрическая сумма токов и, следовательно, МДС в трех фазах должны быть равны нулю, т. е.
. . .
FA FB FC 0 .
Решая написанные уравнения относительно FA , FB и FC , полу-
чаем:
. |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
FA (Rст 2Rя )ФA |
|
3 |
Rя ФB |
; |
|
|
|||||||
|
. |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
FB Rст ФB |
3 |
|
Rя ФB; |
|
(5.2) |
|||||||
. |
|
|
|
|
. |
|
|
2 |
|
. |
|
|
|
F (R |
2R |
|
)Ф |
|
|
R |
Ф ; |
|
|
||||
|
3 |
|
|
||||||||||
C |
ст |
|
я |
|
C |
|
|
я B |
|
|
|
||
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
Из (5.2) следует, что МДС |
|
FB |
|
зависит только от потока |
и |
||||||||
|
|
ФB |
|||||||||||
.
поэтому вектор FB совпадает по фазе с вектором потока ФB . Наобо-
. .
рот, МДС FA и FC представляют собой геометрические суммы двух
МДС, из которых одна совпадает по фазе с данным потоком, а другая –
.
с потоком ФB . Поэтому вектор МДС FA отстает по фазе от вектора
.
потока ФA на некоторый угол, а вектор МДС FC опережает на такой
|
|
|
|
. |
. |
. |
же угол вектор потока |
|
|
FA |
, FB |
и FC и, |
|
ФC . Таким образом, МДС |
||||||
следовательно, намагничивающие токи |
I0А , I0В ,I0C |
образуют несим- |
||||
|
. |
. |
. |
|
|
|
метричные системы, в |
которых FA =FC > FB или |
соответственно |
||||
I0А =I0C > I0В (жирные линии на рис. 5.2).
Несимметрия токов холостого хода сказывается главным образом в трансформаторах малой мощности, где ярмо играет относительно большую роль. Здесь I0А I0С (1,2 1,5)I0В .
В трансформаторах большой мощности несимметрия заметно сглаживается. За ток холостого хода I0 принимают среднее арифме-
тическое значение токов I0А , I0В и I0C . Так как ток I0 невелик (от 3
до 8% Iн ), то даже в трансформаторах малой мощности несимметрия
токов холостого хода перестает сказываться уже при очень небольшой нагрузке.
Так как ток I0В отстает от напряжения UB на 90°, то мощность фазы B равна нулю; мощность фазы C положительна, так как проек-
.
ция тока I0C на направление вектора UC положительна, а мощность фазы A равна мощности фазы C по величине, но обратна по знаку,
.
так как проекция тока I0А на направление вектора UA отрицательна. Таким образом, при холостом ходе трехстержневого трансформатора фазы C и A обмениваются мощностями, но полная мощность холостого хода трансформатора равна нулю, чего и следовало ждать, поскольку мы рассматриваем простейший трансформатор. Неодинаковое распределение мощности при холостом ходе, так же как несимметрия токов, не имеет значения, так как эта мощность обычно меньше 1 % от номинальной мощности трансформатора.
Примером трехфазного трансформатора с независимой магнитной системой служит трехфазная трансформаторная группа, или, проще, групповой трансформатор, представляющий собой три одинаковых однофазных трансформатора, обмотки которых определенным образом соединены между собой.
Примером трансформатора с почти независимой магнитной цепью может служить броневой трансформатор. В дальнейшем мы ограничимся рассмотрением только трехстержневого трансформатора и трехфазной трансформаторной группы.
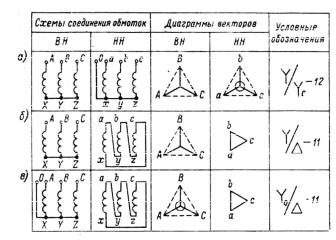
Схемы и группы соединения обмоток. Принятые ГОСТ схемы соединений обмоток трехфазных двухобмоточных трансформаторов показаны на рис. 5.3.
При построении диаграмм линейные напряжения обмотки ВН (штриховые линии на рис. 5.3) изображаются во всех случаях равносторонними треугольниками напряжений, причем вершины А, В и С находятся соответственно в нижнем левом углу, в верхнем углу и в нижнем правом углу. При этом, говоря о работе трансформаторов, мы должны заранее предусмотреть возможность их параллельной работы, при которой могут быть соединены между собой только равнопотенциальные зажимы. Поэтому одного указания на способ соединения обмоток трансформатора недостаточно; необходимо еще указание на угол сдвига между первичным и вторичным линейными напряжениями, в соответствии с чем определяется группа, к которой принадлежит трансформатор.
Рис. 5.3. Схемы соединения обмоток трехфазных двухобмоточных трансформаторов
Покажем, что угол зависит от а) направления, в котором намотана обмотка; б) способа обозначения зажимов обмоток, т. е. их маркировки, и в) способа соединения обмоток трехфазных трансформаторов.
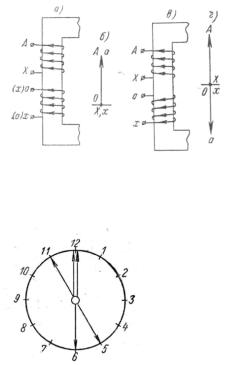
Выясним сначала влияние двух первых факторов на примере однофазного трансформатора. Будем считать, что верхняя обмотка трансформатора на рис. 5.4, a является его первичной обмоткой, а нижняя – вторичной. Предположим, что обе обмотки намотаны в одну и ту же сторону и что их верхние зажимы приняты за начала обмоток и обозначены буквами A и а, а нижние зажимы X и x – за концы обмоток.
Так как обе обмотки трансформатора располагаются на одном и том же стержне и пронизываются одним и тем же основным потоком, то в нашем случае наводимые в обмотках ЭДС имеют в любой момент времени одинаковое направление относительно зажимов обмоток, например от конца X к началу A в первичной обмотке и от конца x к началу а во вторичной обмотке. Соответст-
Рис. 5.4. Угол сдвига векторовЭДС в зависимости отнаправления намотки и обозначения зажимов обмотки.
.
венно этомунапряжения U1 и
.
U2 на зажимах первичной обмотки и вторичной, приведенной к первичной, обмотки трансформатора совпадают по фазе и изображаются двумя
__ __
векторами OA и Oa , равны-
Рис. 5.5.Часовое обозначение группы соединений
ми по величине и одинаково направленными(рис. 5.4, б).
Если первичная и вторичная обмотки намотаны в разные стороны, но сохраняют те же обозначения зажимов, что и на рис. 5.4, а, то, как это можно видеть на рис. 5.4, в, на-
. .
пряжения U1 и U2 относительно зажимов первичной и вторичной обмоток направлены в разные стороны, напри-
мер от X к A в первичной об-мотке и от а кх во вторичной обмотке. Соответственно
. .
этому напряжения U1 и U2 должны быть
__ __
изображены векторами OA и Oa, направленными в разные стороны (рис. 5.4, г).
Мы получили бы такой же результат, если бы, оставив тот же способ намотки обмоток, что и на рис. 5.4, а, изменили маркировку вторичной обмотки, поменяв местами обозначения ее зажимов (соответствующие буквы поставлены в скобках на рис. 5.4, а). В этом случае первичное напряжение было бы направлено в одну сторону, например от зажима X к зажиму A, а вторичное напряжение в другую – от зажима а к зажиму х.
__
Таким образом, принимая вектор OA первичного напряжения за
__
исходный, мы можем сказать, что вектор Oa вторичного напряжения
__
однофазного трансформатора либо совпадает с вектором OA по фазе,
__
либо находится с ним в противофазе; в первом случае вектор Oa сме-
__
щен относительно вектора OA на угол 0 °, а во втором – на угол
180 °
Вместо того чтобы выражать угол сдвига между напряжениями в градусах, удобнее пользоваться часовым способом обозначения угла.
__
Для этого вектор OA первичного линейного напряжения принимают за большую стрелку часов и устанавливают на цифре 12 часового ци-
__
ферблата, а вектор Oa вторичного линейного напряжения принимают за малую стрелку часов и устанавливают на циферблате соответствен-
__ |
__ |
но положению вектора Oa относительно вектора OA . Если векторы
__ __
OA и Oa совпадают по фазе, как на рис. 5.4, б, то малую стрелку часов мы должны установить, как и большую стрелку, на той же цифре 12 (рис. 5.5). Угол сдвига между стрелками часов равен нулю или, что одно и то же, 360° = 30° 12. Здесь угол 30° представляет собой угол между двумя соседними цифрами часового циферблата и принимается за единицу часового сдвига. Цифра 0 и определяет собой группу, к которой в данном случае принадлежит трансформатор.
__ __
Если векторыOA и Oa находятся в противофазе, как на рис. 5.4, г, то малую стрелку часов мы должны установить на цифре 6 циферблата соответственно углу сдвига на 30° 6 = 180°. В этом случае группа трансформатора определяется цифрой 6.
Выясним теперь вопрос о группах трехфазных трансформаторов. Предположим, что обе обмотки трансформатора соединены звез-

дой, намотаны в одну и ту же сторону и имеют одинаковые обозначения зажимов. Обмотку ВН мы будем считать первичной обмоткой, а обмотку НН – вторичной. Системы линейных и фазных первичных и вторичных напряжений предполагаются симметричными. Так как вторичная обмотка как бы повторяет первичную, то звезда ах, by и сz вторичных фазных напряжений и треугольник abc вторичных линейных напряжений совпадают соответственно по фазе со звездой АХ, BY и CZ и треугольником ABC фазных и линейных первичных напряжений (рис. 5.6). Таким образом, угол сдвига вторичного линейного напряжения относительно первичного равен нулю, и, следовательно, трансформатор принадлежит к группе Y /Y 0( 0 °).
Если мы намотаем обмотку НН в обратном направлении относительно обмотки ВН. или поменяем местами ее начала и концы (но неодновременно одно и другое), то при соединении обеих обмоток попрежнему звездой треугольник напряжений abc повернется относительно треугольника ABC на 180°, т. е. на 30° 6 (рис. 5.7). В этом случае вторую стрелку часов надо установить на цифре 6 циферблата (см. рис. 5.5). Следовательно, данное соединение обмоток относится к группе 6 и пишется в виде Y /Y 6 или Y /Y0 6 .
Рис. 5.6. Соединение Y /Y 0
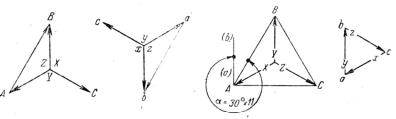
Рассмотрим теперь соединение звезда – треугольник на рис. 5.3, б. Здесь обмотка НН соединена по схеме а–х–с–z–b–y–а. Стороны AB, ВС и СА треугольника напряжений ABC определяют собой линейные напряжения обмотки ВН, а лучи звезды того же треугольника – фазные напряжения этой обмотки. Если обмотки ВН и НН намотаны в одном направлении и имеют одинаковые обозначения зажимов, то векторы фазных напряжений обеих обмоток совпадают. Поэтому при построении треугольника abc нужно провести из точки а (рис. 5.8), находя-
__ |
__ |
щейся в левом нижнем углу, вектор ax параллельно вектору AX , затем из точки с, которую нужно совместить с точкой x, следует провес-
__ |
__ |
ти вектор czпараллельно вектору CZ и, наконец, из точки b, которую
__
нужно совместить с точкой z, провести вектор by параллельно вектору
__
BY , тем самым замыкая треугольник abc. Сопоставляя положения треугольников ABC и abc, например сторон АВ и ab, можно видеть, что второй треугольник повернут относительно первого по направлению вращения часовой стрелки на 330°= 30° 11. Следовательно, данное соединение обмоток относится к группе 11 и пишется в виде Y / 11.
Рис. 5.7. Соединение Y /Y 6 Рис. 5.8. СоединениеY / 11
Если бы обмотка НН была намотана в обратном направлении относительно обмотки ВН или мы поменяли местами ее начала и концы, то треугольник abc повернулся бы относительно треугольника ABC на 150° = 30° 5. Следовательно, такое соединение обмоток дает группу 5 и пишется в видеY / 5 . Нетрудно показать, что если бы мы соединили обмотку НН по схеме а–х–b–у–с–z–a, то при одинаковом направлении намотки и одинаковых обозначениях зажимов получили бы группу Y / 1.
Группы 0, 6, 11 и 5 считаются основными. Из них можно получить ряд производных групп. Для этого нужно только переместить зажимы обмотки НН относительно зажимов обмотки ВН. На рис. 4.15, а обе обмотки соединены звездой и одинаково намотаны, но зажимы а, b, с вторичной обмотки перемещены относительно зажимов А, В, С первичной обмотки на угол 120°; в этом случае треугольник abc повернется относительно треугольника ABC по вращению часовой стрелки на 30° х 4 = 120°, т. е. мы имеем группу соединенийY /Y 4.
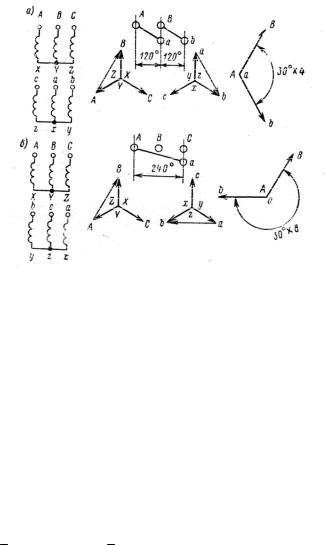
Рис. 5.9. Группы соединений Y /Y 4 и Y /Y 8
Если бы при соблюдении тех же условий мы переместили зажимы а, b, с относительно зажимов А, В, С на 240° (рис. 5.9, б), то получили бы группу соединений Y /Y 8.
В том случае, когда обмотка НН намотана в обратном направлении относительно обмотки ВН, мы получаем группы 10 и 2 соответственно группам 4 и 8.
Таким образом, при соединении обмоток по схеме звезда – звезда получаются все четные группы соединений. Рассуждая аналогично, нетрудно убедиться, что при соединении обмоток по схеме звезда – треугольник получаются все нечетные группы соединений.
Области применения различных способов соединения обмо-
ток. Соединение Y /Y0 0 применяется в тех случаях, когда нагрузка
носит смешанный осветительно-силовой характер. Двигатели включаются на линейное напряжение 220 или 380в, а лампы – между одним из линейных проводов и нейтральным проводом, т.е. на напряжение
220/
 3 =127в или 380/
3 =127в или 380/
 3 =220в.
3 =220в.
Так как при заданном напряжении ток растет пропорционально мощности, то во избежание затруднений, связанных с устройством обмотки на большие токи, ГОСТ ограничивает предельные мощности трансформаторов при соединении Y/Y0 – 0 пределами, указанными в табл. 5.1. Если при этом нагрузка неравномерна, то ток в нейтральном
проводе трансформатора не должен превышать 25% номинального тока обмотки НН
В тех случаях, когда номинальное вторичное напряжение выше 400 в, ГОСТ предусматривает соединение обмоток по способу Y/∆–11. Как будет видно из дальнейшего, соединение одной из обмоток треугольником оказывает ценное положительное влияние на условия работы трансформатора.
Последняя группа трансформаторов, указываемых в табл. 5.1, обслуживает главным образом, линии передачи. Соединение обмоток этих трансформаторов по способу Y0/∆–11 предусматривает возможность заземления системы на стороне высшего напряжения.
Таблица 5.1
Обозначение |
Напряжение обмоток |
|
|
схемы соеди- |
|
|
Мощность транс- |
нения обмоток |
ВН кВ |
НН В |
форматора кВ A |
|
|
|
|
Y/Y0 – 0 |
До 35 (включитель- |
230 |
До 560 (включи- |
|
но) |
|
тельно) |
|
|
400 |
До 1800 (включи- |
|
|
|
тельно) |
|
|
|
|
Y/∆ – 11 |
До 35 (включитель- |
525 |
До 1800 (включи- |
|
но) |
|
тельно) |
|
|
Выше 525 |
До 5600 (включи- |
|
|
|
тельно) |
|
|
|
|
Y0/∆–11 |
110 и выше |
3150 и выше |
3200 и выше |
|
|
|
|
|
6,3 и выше |
3300 и выше |
7500 и выше |
|
|
|
|
Особенности хх трехфазного трансформатора при соедине-
нии его обмоток по способу Y/Y0–0. При изучении режима холостого хода однофазного трансформатора мы видели, что при подведенном синусоидальном напряжении кривые первичной и основного потока синусоидальны, а кривая тока содержит наряду с первой гармонической сильно выраженную третью гармоническую.
Возьмем теперь трансформаторную группу, состоящую из трех одинаковых однофазных трансформаторов, обмотки которых соединены по способу Y/Y0 – 0 (рис. 6.1).
Основное, что отличает работу при холостом ходе такой трансформаторной группы от работы при холостом ходе однофазного
