
- •1. Устойчивость численных методов к ошибкам округления.
- •2. Способы оценки погрешности решения.
- •4. Слау. Устойчивость метода Гаусса. Выбор ведущего элемента.
- •Устойчивость метода Гаусса.
- •Задача численного решения уравнения сводится, во-первых, к отделению корней, во-вторых, к последующему уточнению корней.
- •Лемма об оценке погрешности приближенного решения уравнения .
- •Задача численного решения уравнения сводится, во-первых, к отделению корней, во-вторых, к последующему уточнению корней.
- •Теорема о сходимости и точности метода итераций.
- •8. Снау. Метод итераций.
- •Метод итераций для системы уравнений.
- •Метод Ньютона.
- •Теорема о сходимости и точности метода Ньютона.
- •10. Снау. Метод Ньютона.
- •Метод Ньютона для решения систем нелинейных уравнений.
- •Модификации метода Ньютона. Краткий обзор.
- •11. Интерполяционная формула Лагранжа.
- •Интерполяционная формула Лагранжа.
- •12. Интерполяционная формула Ньютона.
- •Интерполяционная формула Ньютона.
- •14. Вычисление одномерных интегралов. Формула трапеций. (методичка)
- •Постановка задачи.
- •Формула трапеций.
- •15. Вычисление одномерных интегралов. Формула Симпсона. (методичка)
- •Постановка задачи.
- •Формула Симпсона.
- •16. Вычисление двойных интегралов. Формула Симпсона.
- •17. Соду. Явный метод Эйлера. Условие устойчивости. (методичка)
- •Явный метод Эйлера.
- •18. Соду. Неявный метод Эйлера. Устойчивость метода. (методичка)
- •Неявный метод Эйлера.
- •19. Уравнения, описывающие стационарные процессы, процессы переноса, волновые процессы. Постановка краевых задач.
- •20. Метод интегральных тождеств. Kp-аппроксимация стационарного уравнения теплопроводности.
- •21. Метод интегральных тождеств. Kp-аппроксимация нестационарного уравнения теплопроводности.
16. Вычисление двойных интегралов. Формула Симпсона.
Вычислить
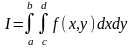 .
.
Область
интегрирования здесь – прямоугольник
со сторонами
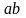 и
и
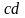 (рис. 12.2). Применим формулу Симпсона,
вычисляя определенный интеграл сначала
по
,
затем по
.
(рис. 12.2). Применим формулу Симпсона,
вычисляя определенный интеграл сначала
по
,
затем по
.
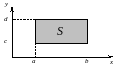
Рис. 12.2. Область интегрирования
Пусть
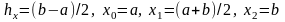 ,
,
и
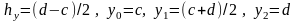 .
.
Тогда
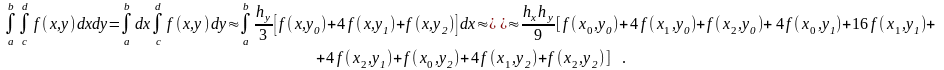
Для повышения точности вычислений область покрывается сетью прямоугольников. В этом случае
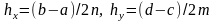 ,
,
и значение двойного интеграла вычисляется в виде
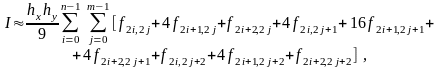
где
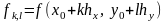 .
.
Если
– криволинейная область, то для применения
полученной формулы Симпсона область
заключают в прямоугольник
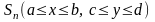 и пользуются вспомогательной функцией
и пользуются вспомогательной функцией

Тогда
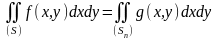
и для вычисления последнего интеграла привлекают метод Симпсона.
17. Соду. Явный метод Эйлера. Условие устойчивости. (методичка)
Явный метод Эйлера.
Рассмотрим
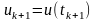 ,
где
,
где
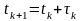 ,
,
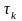 – текущий шаг интегрирования. Разложим
функцию
– текущий шаг интегрирования. Разложим
функцию
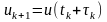 в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки
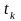 :
:
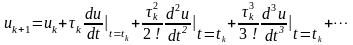 .
.
Ограничившись в этом разложении двумя членами, получим разност-ную схему метода Эйлера
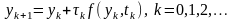 .
.
Локальная погрешность метода Эйлера составляет величину
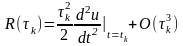 .
.
В вычислительной математике численные методы решения обык-новенных дифференциальных уравнений принято характеризовать порядком точности.
Определение.
Если локальная погрешность численного
метода
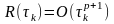 ,то
порядок точности такого метода равен
,то
порядок точности такого метода равен
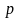 .
.
Метод Эйлера является методом первого порядка.
Приведем геометрическую интерпретацию явного метода Эйлера для задачи Коши
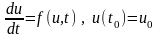
(см. рис. 13.2). Приращение на шаге интегрирования – катет прямоугольного треугольника, лежащий против угла, тангенс которого равен значению производной в предыдущий момент времени. Вторым катетом этого треугольника является текущий шаг интегрирования.
t
u
u0
t1
t0







y0
τ
y1
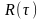
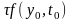
Рис. 13.2. Геометрическая иллюстрация явного метода Эйлера
Оценим устойчивость метода Эйлера по отношению к шагу ин-
тегрирования. Для этого рассмотрим линейную автономную систему
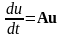
с
отрицательно определенной
 матрицей
простой структуры. Отрицательная
определенность матрицы означает, что
все собствен-ные значения
матрицей
простой структуры. Отрицательная
определенность матрицы означает, что
все собствен-ные значения
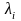 матрицы действительны и отрицательны,
т. е.
матрицы действительны и отрицательны,
т. е.
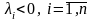 .
В этом случае все решения
.
В этом случае все решения
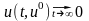 .
.
Применим
для решения этой системы метод Эйлера
с постоянным шагом
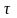 :
:
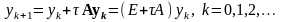 .
.
Здесь E – единичная матрица соответствующей размерности.
Из алгебры известно, что для любой неособенной матрицы простой структуры существует такая неособенная матрица , которая преобразованием подобия приводит матрицу к диагональному виду:
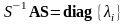 .
.
Преобразуем вычислительную схему метода Эйлера следующим образом:
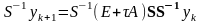 .
.
Введем
замену переменных
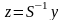 .
Тогда
.
Тогда
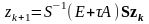 ,
,
или
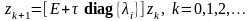 .
.
Запишем это соотношение для i-й компоненты вектора :
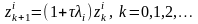 ,
,
или
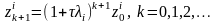 ,
,
где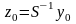 ,
т. е. определяется начальным условием.
,
т. е. определяется начальным условием.
Нетрудно видеть, что
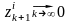 ,
,
если
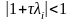 .
Именно этим свойством обладает решение
автономной системы с отрицательно
определенной матрицей. Отсюда приходим
к требованиям
.
Именно этим свойством обладает решение
автономной системы с отрицательно
определенной матрицей. Отсюда приходим
к требованиям
 ,
,
при
этом неравенство
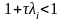 приводит к естественному условию
приводит к естественному условию
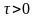 ,
т. к.
,
т. к.
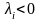 ,
а неравенство
,
а неравенство
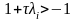
к условию
к условию
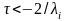 .
.
Очевидно,
чтобы
 ,
необходимо при выборе шага интегрирования
выполнить условие
,
необходимо при выборе шага интегрирования
выполнить условие
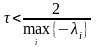 .
.
Таким образом, явный метод Эйлера по отношению к шагу интегрирования является условно устойчивым.
