14. Формула трапеций.

Примем шаг сетки, которой покрывается отрезок интегрирования , постоянным и равным

,

где 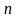– число интервалов разбиения. Узлы интерполяции вычисляются в этом случае по правилу:

,

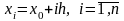причем .

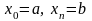Заменим подынтегральную функцию на отрезке 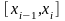интерполяционным многочленом Лагранжа первого порядка:

.

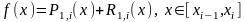Тогда

.

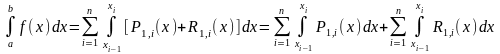Первый член в таком представлении является приближенным значением определенного интеграла, второй – погрешностью расчета.

В частности

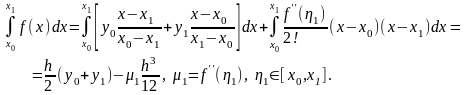Аналогично

Просуммируем

,

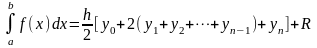где

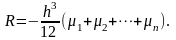
Отсюда следует, что формула трапеций имеет достаточно простой вид:

.

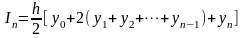При этом ошибка вычисления определенного интеграла не превосходит величины:

,

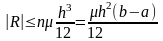где

.

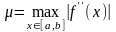Погрешность формулы трапеций имеет второй порядок относительно шага сетки.

Точность вычисления определенного интеграла может быть повышена двумя способами: уменьшением шага сетки, увеличением точности интерполяции подынтегральной функции.

15. Вычисление одномерных интегралов. Формула Симпсона. (методичка)

15. Постановка задачи.

Речь идет о вычислении определенного интеграла

в тех случаях, когда функция задана таблично, либо когда первообразная функции находится очень сложно.

Общая схема построения рассматриваемых вычислительных методов расчета определенных интегралов сводится к следующему.

4. Отрезок интегрирования покрывается сеткой и вычисляются значения функции во всех узлах сетки (рис. 12.1).

Рис. 12.1. Покрытие отрезка интегрирования сеткой

5. Подынтегральная функция на всем отрезке или на его отдельных частях заменяется легко интегрируемой интерполяционной функцией , для которой

.

В качестве интерполяционной функции чаще всего используется по-

линомиальная функция, т. е.

6. Вычисляется приближенное значение определенного интеграла

и оценка погрешности

.

16. Формула Симпсона.

Разобьем интервал интегрирования на четное число частей . В этом случае шаг сетки (шаг интерполирования)

,

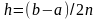и сеточные узлы принимают значения

,

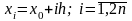при этом .

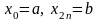Рассмотрим простейший случай, когда сетка содержит только три узла: 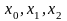. Очевидно, что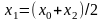 . Вычислим приближенное значение интеграла, заменяя подынтегральную функцию интерполяционным многочленом Лагранжа второго порядка:

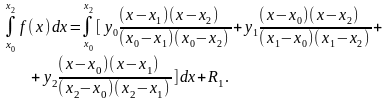
Первый член, составляющий приближенное значение искомого интеграла, легко интегрируется точно. В результате имеем следующее равенство:

,

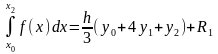где 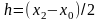, 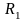– погрешность вычисления интеграла. Таким образом, формула Симпсона для случая трех узлов имеет вид

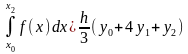. (12.1)

Оценим погрешность . Так как погрешность интерполяции подынтегральной функции многочленом Лагранжа второго порядка пропорциональна третьей производной от подынтегральной функции, то соотношение (12.1) является точным для всех подынтегральных функций, описываемых полиномом второй степени. В силу симметрии эта формула является точной и для подынтегральных функций, описываемых полиномом третьей степени:

,

так как она точна для 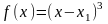. В этом нетрудно убедиться, проверив справедливость равенства

.

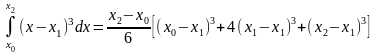Рассмотрим полином третьей степени, удовлетворяющий условиям

.

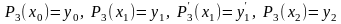Он интерполирует функцию на отрезке 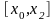по значениям функции в узлах 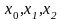и по значению ее производной в узле 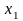(узел имеет кратность два):

,

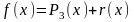где 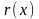– погрешность кратной интерполяции, которая равна

.

(Вывод погрешности кратной интерполяции опустим.) Тогда можем записать, что

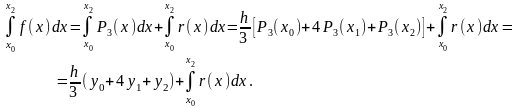Найдем теперь погрешность приближения определенного интеграла:

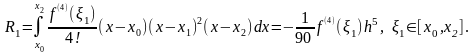
Пусть теперь сетка содержит произвольное число узлов 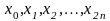, принадлежащих отрезку интегрирования , причем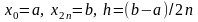 . Последовательно вычислим интеграл на отрезках длиной , интерполируя подынтегральную функцию многочленом Лагранжа второго порядка:

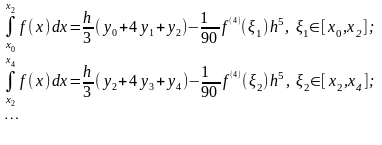
Просуммируем левые и правые части этих соотношений:

,

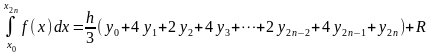где

.

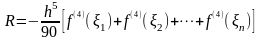Таким образом, формула Симпсона принимает следующий вид:

.

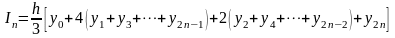Погрешность вычисления определенного интеграла по формуле Симпсона имеет четвертый порядок относительно шага сетки:

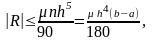
где

.
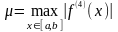