11. Интерполяционная формула Лагранжа.

11. Интерполяционная формула Лагранжа.

При построении интерполяционной формулы Лагранжа в качестве 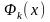используются полиномы Лагранжа 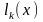степени n, удовлетворяющие условиям

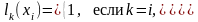
Для выполнения второго условия полином степени n должен иметь вид

,

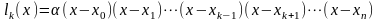т. е. его корнями являются все узлы интерполяции, кроме k-го. Коэффициент определим, используя первое условие:

.

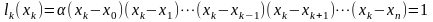Отсюда находим

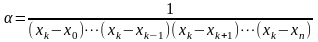
и

.

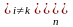Решение системы (10.3) при использовании в качестве элементарных функций полиномов Лагранжа имеет вид 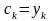. Таким образом, интерполяционный многочлен Лагранжа представится как

.

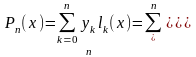Преобразуем его к виду, используемому на практике при вычислении значений функции:

.

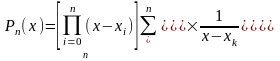Интерполяционный многочлен совпадает с интерполируемой функцией только в точках 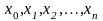. В остальных точках имеет место погрешность интерполяции

,

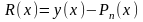которая оценивается величиной

,

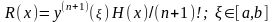где 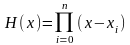. (Вывод оценки погрешности опустим). Погрешность интерполяции зависит от числа узлов интерполяции n, а также от их расположения на отрезке . Наилучшими узлами интерполяции следует признать те 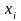, для которых 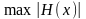принимает наименьшее значение.

Недостатком интерполяционной формулы Лагранжа является то, что каждое слагаемое зависит от всех узлов интерполяции. При добавлении узла интерполяции и, следовательно, повышении порядка полинома необходимо вычислять не только слагаемое, относящееся к новому узлу, но и перевычислять заново слагаемые, относящиеся ко всем узлам интерполяции.

12. Интерполяционная формула Ньютона.

12. Интерполяционная формула Ньютона.

Пусть . Построим первую разделенную разность

.

Откуда находим

.

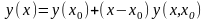Построим вторую разделенную разность

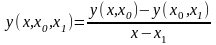
и выразим из нее :

.

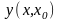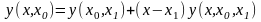Подставим в выражение для :

.

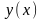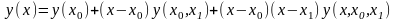Аналогично привлекаем следующие узлы интерполяции для построения интерполяционной функции.

После использования всех узлов интерполяции:

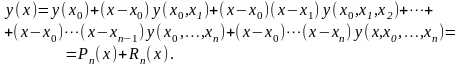Таким образом, интерполяционный многочлен Ньютона имеет вид

.

Непосредственной проверкой нетрудно убедиться, что

.

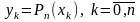Погрешность интерполяции

.

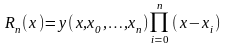Более эффективное вычисление значения функции по интерполяционной формуле Ньютона можно получить, если преобразовать ее к такому виду:

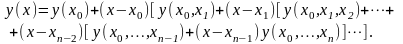
Интерполяционная формула Ньютона позволяет легко наращивать число узлов интерполяции, требуя при этом вычисления лишь дополнительных слагаемых. Например, добавление узла приведет к вычислению слагаемого

.

?13. Приближение функций методом наименьших квадратов. (методичка)

14. Вычисление одномерных интегралов. Формула трапеций. (методичка)

13. Постановка задачи.

Речь идет о вычислении определенного интеграла

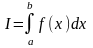
в тех случаях, когда функция задана таблично, либо когда первообразная функции находится очень сложно.

Общая схема построения рассматриваемых вычислительных методов расчета определенных интегралов сводится к следующему.

1. Отрезок интегрирования покрывается сеткой и вычисляются значения функции во всех узлах сетки (рис. 12.1).

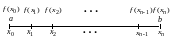
Рис. 12.1. Покрытие отрезка интегрирования сеткой

2. Подынтегральная функция на всем отрезке или на его отдельных частях заменяется легко интегрируемой интерполяционной функцией , для которой

.

В качестве интерполяционной функции чаще всего используется по-

линомиальная функция, т. е.

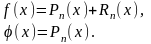
3. Вычисляется приближенное значение определенного интеграла

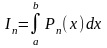
и оценка погрешности

.
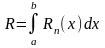