Теорема о сходимости и точности метода Ньютона.
Теорема.
Если уравнение
имеет один корень
,
функци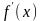и
и
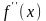– знакопостоянны на этом отрезке,
начальное приближение
выбрано из условия
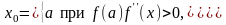
Тогда
последовательность
,
построенная по методу Ньютона, сходится
к точному решению
,
когда
,
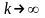при этом справедлива следующая оценка
погрешности:
,
где
.
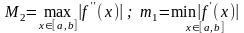Доказательство. Докажем сходимость. Для этого представим:
.
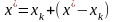Разложим
функцию
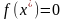в окрестности точки
в ряд Тейлора с остаточным членом в
форме Лагранжа:
,
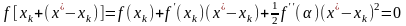где
.
Будем
полагать, что
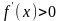и
.
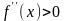В этом случае
,
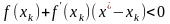так
как
.
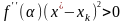Следовательно,
,
или
.
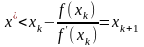Таким
образом,
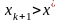и числовая последовательность
ограничена снизу.
Покажем, что последовательность является монотонно убы-
вающей.
Отметим, что невязка
для всех
.
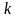Это следует из предположения
и правила выбора в соответствии с
условием теоремы начального приближения.
В этом случае
,
или
.
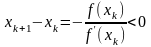Таким
образом,
,
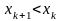а последовательность
является моно-тонно убывающей. Поскольку
монотонно убывающая последователь-ность
ограничена снизу, то она является
сходящейся.
Сходимость метода Ньютона при других вариантах знакопо-стоянства функций и доказывается аналогично.
Получим оценку погрешности. Из леммы
.
Вычислим :
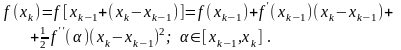
Учтем,
что
.
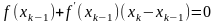Следовательно,
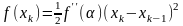
и
.
Теорема полностью доказана.
Замечание.
Величина
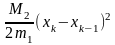является оценкой предельной абсолютной
погрешности метода Ньютона. Она
привлекается при построении критерия
завершения итерационного процесса.
10. Снау. Метод Ньютона.
Метод Ньютона для решения систем нелинейных уравнений.
Пусть задана система нелинейных уравнений
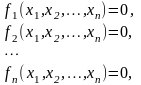
решение
которой достигается в точке
пространства
.
Обозначим
;
.
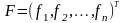Тогда исходная система запишется в виде
.
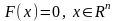Предположим, что известно k-е приближение к . Построим правило Ньютона вычисления (k+1)-го приближения в форме
.
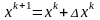Разложим
функцию
в ряд Тейлора в окрестности точки
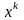и сохраним в разложении два члена:
.
Полагая,
что решение системы достигается на
текущей итерации, относительно поправки
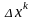получим систему линейных алгебраических
уравнений:
.
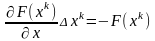Тогда
,
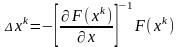и итерационное правило Ньютона решения системы нелинейных алгебраических уравнений запишется как
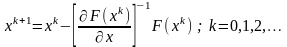
Такой вид метода Ньютона неудобен на практике, потому что требует вычисления обратной матрицы, а эта операция достаточно трудоемка. На практике метод Ньютона реализуется в следующем виде:
Решается система линейных алгебраических уравнений и вычисляется вектор поправки:
,
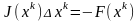где
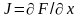– матрица Якоби системы;
Вычисляется (k+1)-е приближение
,
Пункты 1, 2 повторяются для k=0,1,2,… до тех пор, пока не будет достигнута требуемая точность.
Критерием завершения итерационного процесса служат условия
,
,
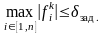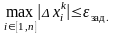или в более общей форме
,
.
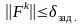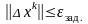Модификации метода Ньютона. Краткий обзор.
Перечислим недостатки метода Ньютона, на устранение которых направлены различные его модификации:
трудность задания начального приближения, от которого метод сходится;
необходимость вычисления на каждой итерации матрицы Якоби, что может потребовать существенных вычислительных затрат;
необходимость решения на каждой итерации системы линейных алгебраических уравнений;
требование невырожденности матрицы Якоби.
Рассмотрим модификации метода Ньютона, которые в той или иной мере устраняют перечисленные недостатки.