
- •1. Устойчивость численных методов к ошибкам округления.
- •2. Способы оценки погрешности решения.
- •4. Слау. Устойчивость метода Гаусса. Выбор ведущего элемента.
- •Устойчивость метода Гаусса.
- •Задача численного решения уравнения сводится, во-первых, к отделению корней, во-вторых, к последующему уточнению корней.
- •Лемма об оценке погрешности приближенного решения уравнения .
- •Задача численного решения уравнения сводится, во-первых, к отделению корней, во-вторых, к последующему уточнению корней.
- •Теорема о сходимости и точности метода итераций.
- •8. Снау. Метод итераций.
- •Метод итераций для системы уравнений.
- •Метод Ньютона.
- •Теорема о сходимости и точности метода Ньютона.
- •10. Снау. Метод Ньютона.
- •Метод Ньютона для решения систем нелинейных уравнений.
- •Модификации метода Ньютона. Краткий обзор.
- •11. Интерполяционная формула Лагранжа.
- •Интерполяционная формула Лагранжа.
- •12. Интерполяционная формула Ньютона.
- •Интерполяционная формула Ньютона.
- •14. Вычисление одномерных интегралов. Формула трапеций. (методичка)
- •Постановка задачи.
- •Формула трапеций.
- •15. Вычисление одномерных интегралов. Формула Симпсона. (методичка)
- •Постановка задачи.
- •Формула Симпсона.
- •16. Вычисление двойных интегралов. Формула Симпсона.
- •17. Соду. Явный метод Эйлера. Условие устойчивости. (методичка)
- •Явный метод Эйлера.
- •18. Соду. Неявный метод Эйлера. Устойчивость метода. (методичка)
- •Неявный метод Эйлера.
- •19. Уравнения, описывающие стационарные процессы, процессы переноса, волновые процессы. Постановка краевых задач.
- •20. Метод интегральных тождеств. Kp-аппроксимация стационарного уравнения теплопроводности.
- •21. Метод интегральных тождеств. Kp-аппроксимация нестационарного уравнения теплопроводности.
8. Снау. Метод итераций.
Метод итераций для системы уравнений.
Пусть необходимо найти решение системы уравнений
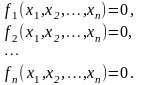
Применение метода итераций требует приведения этой системы к виду:
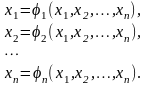
В общем случае это можно сделать так же, как и для одного уравнения:
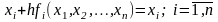 .
.
Отсюда
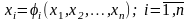 ,
,
где
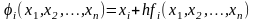 .
.
Параметр
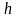 здесь также выбирается из условия
сходимости метода.
здесь также выбирается из условия
сходимости метода.
Метод итераций для системы уравнений приобретает вид
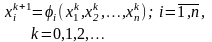
Запишем метод итераций в векторном виде. Обозначим
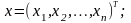 φ
φ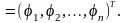
Тогда
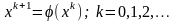 .
.
Рассмотрим, как ведет себя погрешность на итерациях метода. Обозначим через ε вектор погрешности. Очевидно, что
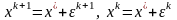 ,
,
где – вектор точного решения. Следовательно,
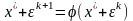 .
.
Разложим правую часть равенства в ряд Тейлора и сохраним в разложении первые два члена:
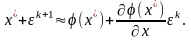
Получим
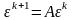 .
.
В этом соотношении
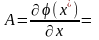
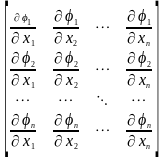 .
.
Пусть
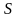 – неособенная матрица, которая
преобразованием подобия приводит
матрицу
к диагональному виду:
– неособенная матрица, которая
преобразованием подобия приводит
матрицу
к диагональному виду:
 ,
,
или
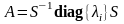 ,
,
где
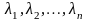 – собственные числа матрицы
.
Тогда
– собственные числа матрицы
.
Тогда
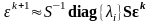 .
.
Введем
новую переменную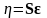 .
Для нее
.
Для нее
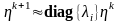 .
.
В компонентном виде имеем:
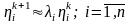 .
.
Если
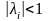 ,
то погрешность
,
то погрешность
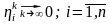 .
Так как
.
Так как
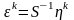 ,
то и
,
то и
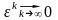 .
Таким образом, условие сходимости метода
итераций для системы уравнений имеет
вид
.
Таким образом, условие сходимости метода
итераций для системы уравнений имеет
вид
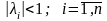 ,
,
где λi– собственные числа матрицы A.
Замечание.
Обозначим собственные числа матрицы
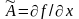 через
через
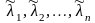 .
Так как
.
Так как
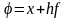 ,
то
,
то
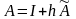 и условие сходимости метода итераций
примет вид
и условие сходимости метода итераций
примет вид
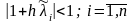 .
.
Предположим,
что все собственные значения матрицы
имеют одинаковый знак, например
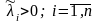 .
В этом случае значения параметра
,
которые обеспечивают сходимость метода
итераций, лежат в интервале
.
В этом случае значения параметра
,
которые обеспечивают сходимость метода
итераций, лежат в интервале
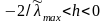 ,
,
где
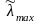 – наибольшее собственное значение
матрицы
.
– наибольшее собственное значение
матрицы
.
9. Уравнение f(x)=0. Метод Ньютона. Теорема о сходимости и точности.
Метод Ньютона.
Рассмотрим
уравнение
,
– корень,
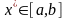 .
Построим итерационное правило уточнения
корня в методе Ньютона.
.
Построим итерационное правило уточнения
корня в методе Ньютона.
Пусть
найдено k-е
приближение
.
Представим
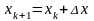 .
Разложим в ряд Тейлора в окрестности
точки
функцию
.
Разложим в ряд Тейлора в окрестности
точки
функцию
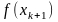 :
:
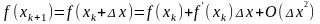 .
.
Полагая,
что
– решение и, ограничившись двумя членами
разложения, относительно поправки
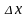 получим уравнение
получим уравнение
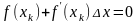 .
.
Отсюда
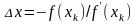 ,
а итерационное правило метода Ньютона
примет вид
,
а итерационное правило метода Ньютона
примет вид
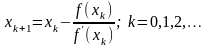 .
.
Здесь – начальное приближение.
Такие
последовательные приближения могут
быть построены, если, во-первых, все
принадлежат области определения функции
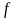 и, во-вторых, для всех xk
выполняется неравенство
и, во-вторых, для всех xk
выполняется неравенство
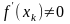 .
.
Г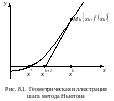 еометрический
смысл правила Ньютона весьма прост. В
плоскости
еометрический
смысл правила Ньютона весьма прост. В
плоскости
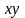 построим график функции
построим график функции
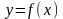 (см. рис. 8.1). Точное решение
будет точкой пересечения этого графика
с осью абсцисс. Рассмотрим на этом
графике точку
(см. рис. 8.1). Точное решение
будет точкой пересечения этого графика
с осью абсцисс. Рассмотрим на этом
графике точку
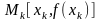 и проведем касательную, проходящую
через точку
и проведем касательную, проходящую
через точку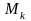 .
Точку пересечения касательной с осью
.
Точку пересечения касательной с осью
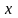 обозначим
.
обозначим
.
Из
треугольника видно, что
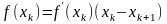 или
или
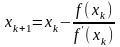 .
.
Геометрическая интерпретация правила Ньютона может быть сформулирована следующим образом: последующее приближение ищется как точка пересечения с осью абсцисс касательной к функции
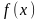 в
предыдущей точке
.
в
предыдущей точке
.
Рассмотрим
теперь, как ведет себя погрешность
решения на двух соседних итерациях.
Обозначим
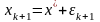 ,
,
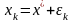 .
Подставим
и
в формулу итерационного процесса:
.
Подставим
и
в формулу итерационного процесса:
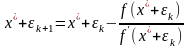 . (◙)
. (◙)
Разложим функции, входящие в это соотношение, в ряд Тейлора в окрестности точки :
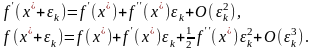
Подставим эти разложения, пренебрегая остаточным членом, в соотношение (◙):
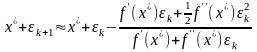 .
.
Выполним очевидное преобразование
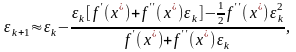
или
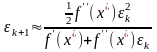 .
.
Членом
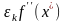 при малых
можно пренебречь. Окончательно
при малых
можно пренебречь. Окончательно
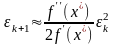 .
.
Говорят, что скорость сходимости метода Ньютона квадратична. Это означает, что если мало, то число правильных десятичных цифр примерно удваивается после каждой итерации. Это свойство является причиной того, что метод Ньютона – наилучший метод общего назначения для решения нелинейных уравнений.
Проведенный анализ устанавливает вероятную сходимость метода Ньютона, т. к. соотношения, связывающие погрешности на двух соседних итерациях, получены путем отбрасывания малых членов. Приведем одну из простых теорем, которая дает условия, достаточные для его сходимости.
