4. Слау. Устойчивость метода Гаусса. Выбор ведущего элемента.

1. Устойчивость метода Гаусса.

Опуская обременительные преобразования в методе обратного анализа ошибок округления, отметим, что возмущенная система метода Гаусса имеет вид

.

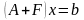Запишем оценку нормы матрицы возмущения:

.

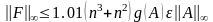Вид этой оценки удовлетворял бы критерию устойчивости Уилкинсона, если бы множитель g(A) имел небольшое значение. Поясним смысл множителя g(A).

Пусть 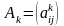обозначает матрицу, полученную из A после k шагов исключения. Обозначим

.

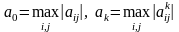Тогда

.

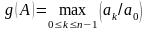Следовательно, g(A) показывает, во сколько раз могут возрасти элементы матрицы A в ходе исключения переменных по сравнению с их исходным уровнем. По этой причине g(A) называют коэффициентом роста матрицы A .

Элементы активной части матрицы A_k в методе Гаусса вычисляются по формуле

.

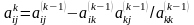Для ограничения роста элементов матрицы в процессе гауссова исключения желательно, чтобы поправочные члены

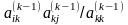
в этой формуле были не слишком большими. Это достигается процедурой выбора элемента 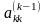, который называют главным.

Выбор главного элемента по столбцу. В этом случае ограничение роста элементов матрицы A_k на k–м шаге гауссова исключения достигается перестановкой строк таким образом, чтобы гарантировать неравенство

.

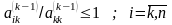С этой целью при исключении переменной 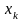в качестве главного элемента выбирается элемент 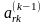матрицы A_k-1 по правилу

,

т. е. наибольший по модулю элемент в k–м столбце матрицы A_k-1 (рис. 3.1). Строки r и k переставляются и только после этого выполняется k–й шаг исключения прямого хода Гаусса.

П ри столбцовой стратегии выбора главных элементов справедлива такая оценка для значения параметра a_k, определяющего коэффициент роста:

.

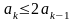Она допускает, что 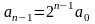и, следовательно, коэффициент роста

.

По этой причине метод Гаусса с выбором главного элемента по столбцам является условно устойчивым. Несмотря на это, он широко используется на практике, так как g(A) редко достигает своего верхнего предела.

Выбор главного элемента по всей матрице. В этой стратегии в качестве главного элемента при исключении неизвестной x_k выбирается элемент 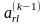по правилу

,

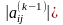т. е. наибольший по модулю элемент в квадратной 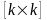подматрице матрицы A_k-1 (рис. 3.2). Строки k и r, а также столбцы k и l переставляются и далее выполняется k–й шаг исключения. Такая стратегия гарантирует выполнение неравенства

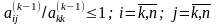
и, следовательно, ограничивает рост элементов в процессе исключения Гаусса.

Оценка коэффициента роста элементов матрицы A в этом случае имеет более благоприятный вид:

.

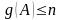?5. СЛАУ. Точность метода Гаусса. Направления повышенной точности.

Точность метода Гаусса.

Привлекая оценку нормы матрицы возмущения, можно записать, что

.

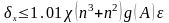Анализ неравенства позволяет определить пути повышения точности метода Гаусса: выбор главных элементов, работа с числами удвоенной длины, переобусловливание системы линейных алгебраических уравнений.

6. Уравнение f(x)=0. Лемма об оценке погрешности приближенного решения.

Пусть требуется решить уравнение

,

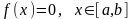т. е. найти все корни 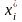, удовлетворяющие этому уравнению на отрезке .
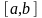