1. Устойчивость численных методов к ошибкам округления.
Устойчивость.
Пусть последовательность величин
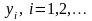вычисляется по рекурсивному правилу
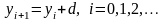
при
заданных
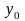и d.
Предположим,
что при вычислении
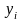внесена ошибка i
(например, за
счет операции округления), т. е. вместо
значения
используется приближенное
значение
.
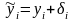В соответствии с рекурсивным правилом
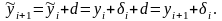
Следовательно,
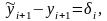
и ошибка, допущенная на i-м шаге процесса, на следующем шаге не увеличивается, если операция сложения выполнена без новых округлений. Это означает, что алгоритм устойчив.
Рассмотрим другое рекурсивное правило вычисления этой последовательности:
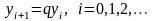
Опять y0 и q считаем заданными.
Пусть, как и в предыдущем примере,
.
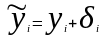Тогда
,
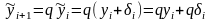или
.
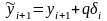В этом случае
,
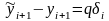и при q>1 ошибка будет возрастать. Такой алгоритм является неустойчивым.
2. Способы оценки погрешности решения.
Точность. Обозначим через y точное решение задачи, yk – ее приближенное значение, полученное на k-м шаге численного метода. Тогда
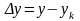
составляет погрешность решения, а
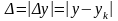
является абсолютной погрешностью.
Вычислительный
алгоритм должен давать решение с заданной
точностью
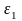и, следовательно, критерием завершения
процесса уточнения решения является
выполнение неравенства
.
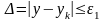На практике в силу трудностей вычисления абсолютной погрешности вместо используют ее оценку сверху – предельную абсолютную погрешность Δy. В качестве Δy выбирают как можно меньшее значение, удовлетворяющее неравенству
,
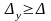а критерием завершения процесса в этом случае является неравенство
.
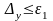Часто используют относительную погрешность
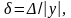
т. е. абсолютную погрешность на единицу измерения, и предельную относительную погрешность
.
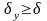Критерий завершения процесса в этом случае имеет вид
,
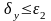где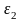
– заданная допустимая относительная
ошибка.
Рассмотрим в качестве примера, как может быть построена оценка предельной абсолютной погрешности вычисления значений функции
,
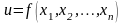если
известны абсолютные погрешности
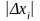ее аргументов.
Ошибка имеет вид
.
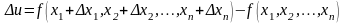Тогда
,
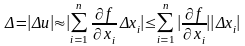и в качестве предельной относительной погрешности можно использовать величину
.
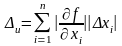Пусть решением задачи является вектор
,
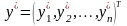который
будем рассматривать как элемент
векторного пространства
.
Приближенное решение
и его погрешность
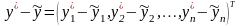
также являются элементами этого пространства. Рассмотрим, как оцениваются ошибки решения в этом случае. Для этого используем количественную характеристику вектора в виде нормы.
Говорят,
что в
задана норма, если каждому вектору
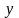из
сопоставляется вещественное число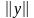
,
называемое нормой вектора
,
для которого справедливы следующие
свойства:
,
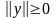причем
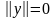тогда и только тогда, когда
,
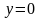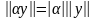для
любого вектора
и любого числа ,
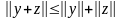для
любых векторов
и
.
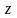В вычислительных методах наиболее употребительны следующие нормы:
.
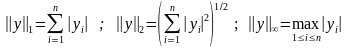Абсолютную и относительную погрешность вектора в любой из перечисленных выше норм можно определить следующим образом:
.
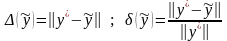Имеет
смысл говорить об абсолютной и
относительной погрешности (mn)-
матрицы решений A.
В этом случае используется такая
характеристика, как норма матрицы,
согласованная с нормой вектора. Для
нормы матрицы A,
обозначаемой
,
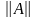справедливы
следующие свойства:
,
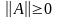причем
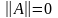тогда и только тогда, когда
,
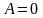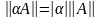для
любой матрицы A
и любого числа
,
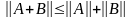для
любых (mn)-матриц
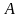и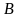
.
Каждой
из векторных норм соответствует своя
согласованная норма матриц. В
частности, нормам
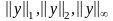соответствуют нормы
,
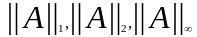вычисляемые
по правилам
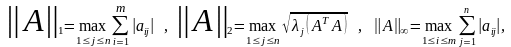
где j(ATA) – собственные числа матрицы ATA.
Абсолютная и относительная погрешности матрицы решений вычисляются через соответствующие нормы:
,
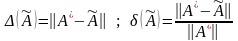причем
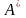– искомая матрица решений,
–
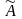ее некоторое приближение.
?3. СЛАУ. Метод Гаусса и оценка его эффективности.