Вычисление дифференциала функции

Дифференциалом функции у=f(x) называется произведение производной этой функции на произвольное приращение аргумента :

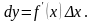
Дифференциал аргумента равен приращению аргумен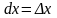та : . Поэтому дифференциал функции равен произведению её производной на дифференциал аргумента:

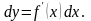
Дифференциалом второго порядка называется дифференциал от дифференциала первого порядка: , т.е. дифференциал второго порядка функции у=f(x) равен произведению второй производной этой функции на квадрат дифференциала аргумента.

Пример1

Найти дифференциалы первого порядка следующих функций:

1. 

2. 

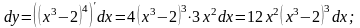
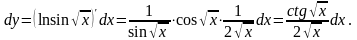
Применение производной к исследованию функции

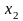Функция y=f(x) называется возрастающей в промежутке , если для любых и , принадлежащих этому промежутку и таких , что < , имеет место неравенство .

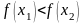Функция y=f(x) называется убывающей в промежутке , если для любых и , принадлежащих этому промежутку и таких , что < , имеет место неравенство .

Как возрастающие, так и убывающие функции называются монотонными, а промежутки, в которых функция возрастает или убывает, - промежутками монотонности.

Возрастание и убывание функции y=f(x) характеризуется знаком её производной.

Теорема

Для того чтобы дифференцируемая на функция y=f(x) не убывала (не возрастала) на этом интервале, необходимо и достаточно чтобы для всех х из этого интервала.

Если же для любого х из то функция y=f(x) монотонно возрастает (монотонно убывает) на этом интервале.

Из теоремы следует, что для того чтобы функция y=f(x) была постоянной на , необходимо и достаточно, чтобы выполнялось условие:

Внутренние точки области определения, в которых производная не существует или равна нулю, называются критическими.

Точка из области определения D(f) точкой максимума (минимума) этой функции, если существует такой интервал , , не выходящий из области определения D(f), что для всех х ≠ , выполняется неравенство

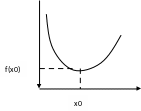
Точки максимума и минимума функции называются точками экстремума, а значения функции в этих точках – экстремумы функции.

Следующая теорема показывает, что точки экстремума следует искать среди критических точек функции.

Теорема Ферма

Если точка - точка экстремума функции y=f(x) и в этой точке существует производная, то

Точки перегиба. Необходимое условие точек перегиба

Определение. Точка из D(f) функции f(x) называется точкой перегиба, если:

1.в этой точке функция непрерывна;

2.существует интервал (а;b), такой, что на интервалах направления выпуклости противоположны, т.е. в точке выпуклость сменяется вогнутостью или наоборот.

Теорема. (необходимое условие точки перегиба)

Пусть дана функция у=f(x) дважды дифференцируемая на (а;b). Если в точке график имеет перегиб и существует конечная вторая производная , то =0.

Схема исследования функции

1. Найти область определения функции.

2. Четность, периодичность.

3. Исследовать функцию на непрерывность: наличие точек разрыва, их характеристика; асимптоты графика.

4. Найти точки пересечения графика с осями координат.

5. Определить критические точки, промежутки возрастания и убывания функции, а также экстремумы функции.

6. Найти интервалы выпуклости и вогнутости, точки перегиба.

7. Построение графика.

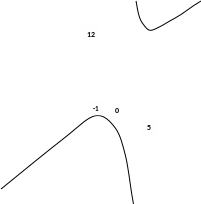
Пример.

Построить график функции

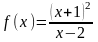
1.

2.Функция не является ни чётной ни нечётной; кроме того, она не является периодической.

3.Функция непрерывна в области определения.

х=2 – точка разрыва

Исследуем функцию в окрестности точки х=2

Следовательно, х=2 – вертикальная асимптота

Найдем наклонные:

является наклонной асимптотой графика функции.

4. (0; ), (-1;0) – точки пересечения с координатными осями.

5.

- критические точки.

+ - - +

Найдем экстремумы функции:

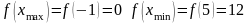
6.

Вторая производная в нуль не обращается на всей области определения функции.

- +

7.Построим график функции: