Метод Гаусса

Рассмотренные методы применимы только для решения систем n линейных уравнений с n неизвестными, имеющих невырожденную матрицу коэффициентов. Универсальным методом решения систем является метод Гаусса, который основан на приведении расширенной матрицы системы с помощью элементарных преобразований к трапецевидной форме.

Если матрицу системы дополнить столбцом свободных членов, то она будет называться расширенной.

Метод Гаусса рассмотрим на примере решения системы:

Составляем расширенную матрицу системы . Элемент (если , то на первое место мы поставим уравнение, в котором коэффициент при ). принимаем за разрешающий. Выполняем шаг гауссовского исключения: разрешающую строку переписываем без изменения, в разрешающем столбце все коэффициенты ниже разрешающего заменяем нулями. Остальные элементы пересчитываем по правилу прямоугольника.

Преобразовав таким образом все уравнения системы, придем к системе, эквивалентной данной. Этим завершается первый шаг гауссовского преобразования, результатом которого стало исключение х из всех уравнений, начиная со второго. Коэффициент при переменной, которую исключаем, называем разрешающим.

Во втором шаге исключений разрешающим является элемент 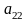. Первые две строки переписываем без изменений, коэффициенты, находящиеся ниже разрешающего обращаются в нули, остальные – пересчитываем по правилу прямоугольника.

По последней матрице записываем систему уравнений, равносильную данной

Из последнего уравнения находим z=1, подставляя найденное значение во второе уравнение, вычисляем y=-1 и из первого уравнения х=2. Итак, 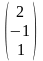- единственное решение данной системы.

Понятие предела функции в точке

Определение предела функции в точке:

Число А называется пределом функции у = f(x) в точке , если для любой последовательности ( ), все члены которой принадлежат области определения функции, стремятся к , но не совпадают с ним соответствующая последовательность значений функции стремится к точке А.

Теорема (необходимое условие существования предела функции в точке):

Функция у=f(x) имеет предел в точке тогда и только тогда, когда в этой точке существует правый и левый пределы и они равны. В этом случае их общее значение и является пределом функции f(x) в точке .

Теоремы о пределах функции в точке

1° Функция в точке может иметь только один предел.

2° Если то

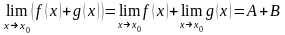
3°

4°

5° Если

Пример

Раскрытие неопределенности вида

Пример. =

Находя предел числителя и знаменателя, получаем . Говорят, что имеем неопределенность вида . Раскрыть неопределенность – значит вычислить предел. Для этого предварительно числитель и знаменатель данной дроби раскладываем на множители.

= = =1.

Определения бесконечно малой и бесконечно большой величин

Если в точке а, то функция f(x) называется бесконечно малой(БМФ) в точке а (функция g(x) называется бесконечно большой (ББФ) в точке а)

Теорема

Если f(x) – БМФ, то - ББФ. Если g(x) – ББФ, то - БМФ.

Пример

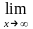
Первый замечательный предел

• Пример

Второй замечательный предел

Пример

= = .
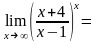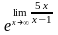