3. Сфера применения высших финансовых вычислений

Раньше мы рассматривали примеры расчеты эффективности отдельных сделок, но финансовыми сделками чаще предусматриваются не отдельные выплаты или поступления, а ряд (поток) платежей. Поток финансовых платежей с постоянными временными интервалами по выплате доходов называется финансовой рентой. Примером финансовой ренты является получение или уплата аренды.

Рассмотрим основные элементы финансовых рент:

- член ренты – величина отдельного платежа;

- период ренты – интервал времени между двумя платежами;

- срок ренты – время от начала финансовой ренты до конца последнего ее периода;

- процентная ставка – ставка, используемая при расчете наращения или дисконтирования платежей, из которых состоит рента.

Классификация рент:

I. По периодичности выплат:

- дискретные ренты в зависимости от сроков выплат бывают годовые или р-срочные (р – число выплат или поступлений в течение года)(через длительные интервалы – аннуитет).

- непрерывные ренты (ежедневные или с короткими промежутками).

2. По обязательности выплат:

- верные ренты платежи носят обязательный характер;

- условные ренты (связаны с выполнением или возникновением каких-то условий или событий);

3. По срокам:

- конечные ренты (ограниченные во времени, суммой выплат и т.п.);

- бесконечные или вечные ренты (заранее не оговорен срок ее окончания;

4. По характеру выплат:

- постнумерандо (выплата проводится в конце периода);

- пренумерандо (выплаты проводятся в начале периода);

5. В зависимости от начала срока ренты различают:

- немедленные (срок выплат начинается с момента контракта, хозяйственной операции);

- отсроченные (начало срока выплат отодвигается на некоторое время от начала сделки).

При определении эффективности финансовых рент обычно возникает вопрос определения обобщающих характеристик – наращенной суммы ренты и современной (приведенной) величины ренты. Наращенная сумма ренты представляет сумму всех членов ренты с начисленными на них процентами к концу ее срока. Современная величина ренты – это сумма всех ее членов, дисконтированных на начало срока ренты.

Рассмотрим примеры расчета финансовых рент.

А. Периодическое помещение на счет одинаковых сумм

Фирме необходимо накопить на банковском счете сумму путем периодического – в конце каждого года – помещения одинаковой суммы. Платеж обозначим РМТ (сокращение от английского слова payment- выплата) – размер ежегодных (одинаковых) выплат. Требуется определить, какая сумма FV накопится через n лет.

Такой вид накоплений возникает, например, при реинвестировании купонных доходов по облигациям или дивидендов по привилегированным акциям.

Особенностью данного вида накопления является то, что начиная со второго периода и далее, проценты начисляются как на общую сумму помещенных вкладов, так и на накопленные за предыдущие периоды проценты. Тогда в конце первого года (первая выплата) на счете будет сумма

FV₁ = PMT

Спустя год (в конце второго года) эта сумма вырастет в 1+i раз и к ней прибавится вторая выплата. Таким образом, в конце второго года на счете будет сумма

FV₂ = PMT(1+i)+PMT.

Правая часть уравнения представляет собой сумму геометрической прогрессии. Путем определенных преобразований получим:

По этой формуле мы определяем величину суммы, накопленной на счете через n лет.

Пример 6. 10000 руб. ежегодно помещаются на банковский счет с начислением 12% годовых в течение 5 лет. Какова будет сумма средств на счете?

FV= 10000 (1+0,12)⁵ – 1/0,12 = 63530 руб.

Пример 7. Ежегодный доход от аренды недвижимости в 150000 руб. инвестируется посредством помещения на банковский счет под 10% годовых в течение 3 лет. Какая сумма накопится на счете в результате инвестирования?

FV =150000(1+0,1)³-1/0,1 =496500 руб.

Б. Формирование фонда погашения.

Теперь рассмотрим задачу, являющуюся обратной к задаче, рассмотренной выше.

Нам необходимо накопить на банковском счете за n лет требуемую сумму FV. Накопление происходит путем периодического в конце каждого года- помещения одинаковой суммы РМТ. Требуется определить величину ежегодных РМТ. При данном виде вклада проценты также начисляются как на общую сумму помещенных вкладов, так и на накопленные за предыдущие периоды проценты

Для расчета накопительного фонда проводим преобразование предыдущей формулы и получаем:

РМТ

Пример 8. Для погашения выпущенного облигационного займа фирме необходимо за 5 лет накопить 150 млн.руб. Рассчитайте размер ежегодных отчислений в банк под 10% годовых.

РМТ = 150*0,1/(1+0,1)⁵ -1 = 24,57 млн. руб.

Показывает какая сумма должна зарабатываться предприятием в год и отчисляться в банк.

В. Погашение долгосрочного кредита равными срочными платежами.

Примером такого кредита является так называемая стандартная ипотечная ссуда – кредит выдается под залог имущества и погашается должником равными выплатами (годовыми, квартальными, ежемесячными). Кредит можем гасить равными суммами плюс проценты, накопившиеся за период с прошлых выплат, или равными срочными платежами, в которых меняются пропорции между погашением основной суммы долга и погашением процентов за кредит.

Пример 9. Получен долгосрочный кредит 20000 тыс. руб. сроком на пять лет под 20% годовых с условием его равномерного возврата платежами раз в год. Необходимо составить план погашения кредита по первому и второму варианту.

Составим план погашения кредита равными суммами. Ежегодная сумма погашения основного долга равна 20000:5 = 4000 тыс.руб. Проценты начисляются на остаток вклада.

План погашения кредита равными суммами

Табл. 4.1.

Номер года	Остаток долга на начало года	Сумма погашения основного долга	Платежи по процентам	Срочная уплата
1	20000	4000	4000	8000
2	16000	4000	3200	7200
3	12000	4000	2400	6400
4	8000	4000	1600	5600
5	4000	4000	800	4800
Итого		20000	1200	32000

При втором варианте погашения кредита общая сумма задолженности ускоренно убывает, а, следовательно, уменьшается и сумма начисленных процентов и увеличивается сумма погашения долга. Поэтому в плане погашения кредита необходимо определять на каждый год наряду с величиной срочного платежа его составные элементы.

Путем определенного преобразования ранее рассмотренных формул получаем формулу определения величины равного срочного платежа

РМТ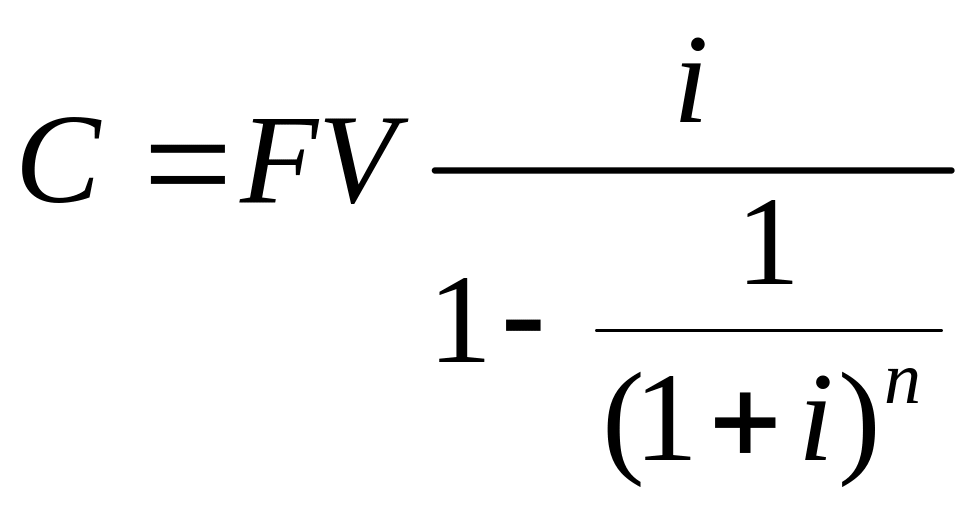

где, РМТ – величина равного срочного платежа;

FV – сумма кредита без процентов.

i – ставка процента, под который получен кредит.

n – срок кредита.

Составим второй вариант плана погашения кредита. По приведенной формуле на основе исходных данных определим сумму равного срочного платежа. РМТ = 6687,6 тыс. руб.

План погашения кредита равными срочными платежами

Табл. 4.2.

Номер года	Остаток долга на начало года	Сумма погашения основного долга	Платежи по процентам	Срочная уплата
1	20000	2687,6	4000	6687,6
2	17312,4	3225,12	3462,48	6687,6
3	14087,28	3870,14	2817,46	6687,6
4	10217,14	4644,17	2043,43	6687,6
5	5572,97	5572,97	1114,63	6687,6
Итого

При выборе вариантов погашения кредита сравнивают современные величины расходов. Для должника предпочтительнее вариант с наименьшей современной величиной расходов, а кредитор при выборе варианта исходит из доходности сделки, т.е. учитывается временная стоимость складывающихся денежных потоков.

Г. Определение современной стоимости аннуитета.

Примерами аннуитета могут являться: доход, приносимый облигацией с постоянным купонным доходом, дивиденды по привилегированным акциям, доход, который приносит сданная в аренду недвижимость. Как отмечалось ранее, доходы, получаемые в разные моменты времени, имеют разную стоимость. Современная стоимость аннуитета, таким образом, складывается из современных (приведенных) стоимостей всех будущих доходов.

Расчет современной стоимости аннуитета может проводиться по двум вариантам:

Первый вариант

Показывает сегодняшнюю стоимость PV будущих платежей FV( РМТ) в течение периода n.

Второй вариант

PV = PMT

Пример 10. Вы являетесь держателем облигации, приносящей на протяжении 5 лет неизменный ежегодный доход в размере 1000 рублей. Какова текущая стоимость облигации, если е доходность составляет 10%.

Решение. PV=3793 руб.

Сравнивая полученный результат с рыночной стоимостью облигации можно сделать вывод о том, облигация переоценена или недооценена.

Пример 11. Вам предлагают два варианта возврата долга взятого на три года. По первому варианту через три года вернуть разовым платежом 35 тыс.руб. По второму возвращать в течение трех лет ежегодно по 10 тыс. руб. Ссуда дана в долг по 20%. Какой вариант погашения долга выбрать?

Определяем современную стоимость долга по первому и второму варианту.

PV₁= 20,25 тыс.руб. PV₂ = 21,06 тыс.руб.

Поскольку современная стоимость долга при втором варианте выше, то его и следует выбрать.

Аналогично проводится расчет, если вам предлагают вернуть долг полностью сегодня. Если сумма возврата будет меньше, чем 20,25 тыс. руб. то предложение необходимо отклонить, если равна 20,25 тыс. руб. или больше стоит принять.