Тема 4: Методы высших финансовых вычислений.

1. Понятие и задачи высших финансовых вычислений.

2. Расчеты по простым и сложным процентам.

3. Сфера применения высших финансовых вычислений.

1. Понятие и задачи высших финансовых вычислений

В результате своего движения стоимость денег меняется во времени. Обладатель денег может инвестировать их в различные проекты с целью получения дохода в будущем. Очевидно, что инвестор ожидает получить сумму, превосходящую его вложения, т.е. предполагает, что деньги будут расти со временем.

Высшие финансовые вычисления – система специальных расчетов связанная с определением стоимости денег в заданный момент времени путем анализа приращения или дисконтирования капитала, иначе говоря, определение изменения стоимости денег, происходящее вследствие их движения в процессе воспроизводства. Поэтому финансовые вычисления называют еще теорией стоимости денег во времени (time value of money – TVM).

Необходимость в таких расчетах возникает при получении предприятиями долгосрочных и краткосрочных ссуд, предоставлении и получении внешних займов и кредитов, покупке и продаже ценных бумаг, оценке эффективности финансовых сделок и т.д.

Прежде мы говорили об анализе свершившихся фактов, а высшие финансовые вычисления направлены на анализ еще не свершившихся фактов. Высшие финансовые вычисления предшествуют событиям. Наращение- это процесс определения будущей стоимости денег на основе известной первоначальной величины. Дисконтирование – определение современной стоимости денег на основе известной будущей величины.

Чтобы провести необходимые вычисления введем следующие обозначения:

PV (present value) – текущая (современная) стоимость, сумма, которой владелец обладает сегодня.

FV (future value) – будущая стоимость денег, сумма которую владелец получит спустя определенное время.

n – время сделки.

i – доходность по сделке, обозначает прирост первоначальной суммы (обычные проценты или проценты постнумерандо – эти проценты начисляются в конце периода относительно исходной величины средств.

d – ставки авансовые или дисконтные (ставки пренумерандо) – устанавливаются в отношении будущей стоимости, а доходы по сделке выплачиваются в начале периода.

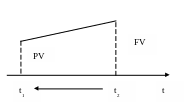
Зная FV, определяем PV на основе дисконтирования.

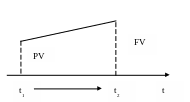
Зная PV, определяем FV на основе наращения.

Механизм финансовых вычислений основан на использовании в расчетах простых и сложных процентов. Поэтому, прежде всего, необходимо разобраться в понятиях простых и сложных процентов, сфере их применения, а также в других исходных понятиях финансовых вычислений.

1. Расчеты по простым и сложным процентам.

3.1. Простые проценты. Расчеты по простым процентам.

Простые процентные вычисления применяются в финансовых обязательствах, заключаемых, как правило, на срок не больше одного года. Сложились математические и банковские методы расчета. Первые основаны на использовании ставки i, вторые – на использовании ставки d.

Они построены на простых арифметических отношениях. При простых процентах расчеты производятся исходя из постоянной базы, в качестве которой выступает первоначальная сумма долга.

А) математические вычисления

Определение будущей стоимости при обычных процентах проводится по следующей формуле:

(1)

где, (1+in) – коэффициент наращения.

Пример 1. 10000 руб. помещаются на счет под 12% годовых, с условием начисления процентов один раз в год. Какова будет стоимость вклада по истечении 1 года, 5 лет?

А) 10000 * (1+ 0.12*1) = 11200 руб.

Б) 10000* (1+ 0.12*5) = 16000 руб.

Определение современной стоимости денег (дисконтирование) проводится по следующей формуле:

, (2)

где - коэффициент дисконтирования.

Он является обратным коэффициенту наращения. В задачах о дисконтировании процентную ставку i называют ставкой дисконтирования. Другое название ставки дисконтирования – ставка альтернативного капитала, ставка альтернативного вложения или ставка альтернативной доходности.

Рассмотрим теперь задачу, обратную той, что рассматривалась в предыдущем примере.

Пример 2. Пусть требуется накопить через год определенную сумму денег, FV – 11200 руб.; через пять лет – 16000 руб. Банк принимает вклады по ставке 12%. Какую сумму надо иметь сегодня для того, чтобы при помещении ее в банк получить через заданный момент времени (1 год, 5 лет) необходимую сумму.

А) 11200*1/1+0,12*1 = 10000 руб.

Б) 16000*1/1+0,12*5 = 10000 руб.

Для того чтобы пояснить различные названия ставки дисконтирования рассмотри простые примеры. Допустим, вы должны получить определенную сумму денег FV через n лет. С другой стороны, вместо этого вы можете получить эквивалент этой суммы PV этой суммы сегодня. Как оценить величину эквивалентной суммы? Полученную сегодня сумму денег PV можно инвестировать в какой-либо проект, в частности вложить в банк под i процентов годовых (альтернативное вложение). Сегодняшний эквивалент суммы FV, полученной через n лет равен, таким образом, величине, определяемой по формуле (2). Или, вам предлагают инвестировать средства в инвестиционный проект, который спустя n лет принесет доход, равный FV. Какую сумму вы согласитесь инвестировать в данный проект? Для того, чтобы ответить на этот вопрос, следует сравнить предлагаемый проект с другими альтернативными вложениями.

Дисконтирование – важная процедура при проведении финансовых расчетов. Метод дисконтирования широко используется для определения современной рыночной стоимости объекта инвестиций, в частности для определения текущей стоимости ценных бумаг.

Процесс дисконтирования позволяет также сравнивать различные доходы, полученные в разное время, путем приведения стоимости этих будущих денежных потоков к настоящему моменту.

Б) банковские (коммерческие) вычисления

При этих вычислениях используется другой подход – за базу (100%) принимается конечная сумма. Согласно этому методу проценты за пользование ссудой начисляются в начале на сумму, подлежащую возврату в конце периода, и определяется по формуле:

(3)

Пример 3. Банк выдает фирме ссуду на 1 год с обязательством погашения в размере 500000 руб. с немедленным удержанием процентов по дисконтной ставке 20%. Какую сумму получит фирма?

Решение: PV= 500000(1- 0, 2) = 400000 руб.

Также данная ставка используется при учете векселей банками. Вексель можно продать в любом финансовом учреждении до срока, указанного на нем, но по цене ниже номинальной. Иначе говоря, вексель реализуется с дисконтом. Дисконт – это разница между номинальной стоимостью векселя и суммой, которую получит владелец векселя в финансовом учреждении при его учете (продаже). Следовательно, прежде чем предъявлять вексель к учету, финансовый менеджер должен оценить эффективность для него данной сделки.

Пример 4. Владелец векселя номинальной стоимостью 20000 руб. со сроком погашения 27декабря 2003г. Собирается реализовать его в банке 20 октября 2003года. Банк согласен учесть вексель с дисконтом 30%. Какую сумму получит владелец векселя?

Решение: 27декабря – 362 день года, день погашения; 20октября -294 день года, день учета. Следовательно, вексель продается за 68 дней до его погашения (362-294).

PV= 20000(1-0,30*68/360) =18866,7 руб.

Дисконт = 20000-18866,7=1133,3 руб.

Таким образом, владелец векселя получит 18866,7 руб., банк получит от векселедателя 27декабря 20000 руб., доход банка составит 1133,3 руб.

Ставки, применяемые при обычном и банковском учете, решают практически одни и те же задачи – определение величины PV по заданной FV. На практике возникает необходимость сравнить эффективность сделок со ставками i и d. Для этого необходимо установить связь между этими ставками, выразив одну через другую

Связь i и d:

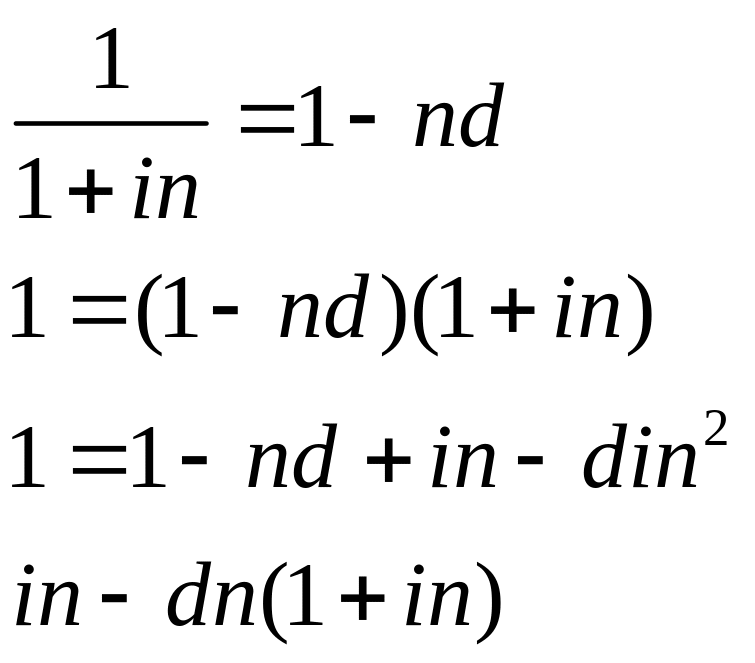
При n имеем:

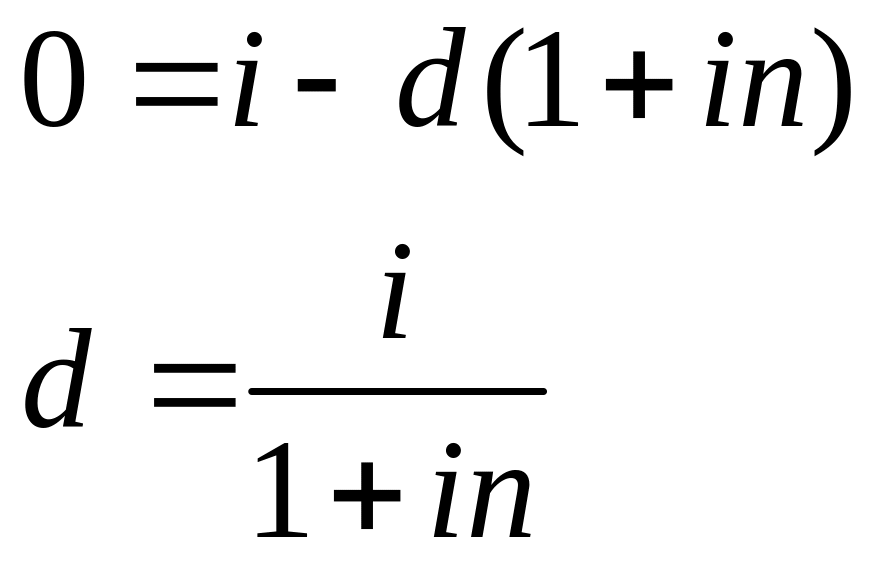
Эти выражения позволяют определить обычную процентную ставку по известной учетной ставке или учетную ставку по известной обычной ставке. Таки образом мы получаем различные по величине процентные ставки, которые дают одну и туже дисконтированную величину платежа при фиксированном сроке ссуды. Такие ставки называют эквивалентными. Они используются при сравнении доходности сделок.

Поскольку ставки дисконтные используются в практике достаточно редко, то все остальные расчеты мы будем проводить на основе обычных ставок.