6. Матричный методы решения система линейных уравнений. Теорема Кронекера-Капелли

Определение Системой m линейных уравнений с n переменными называется система вида

,

где a_ij, b_i, , - произвольные числа, называемые, соответственно, коэффициентами при переменных и свободными членами уравнений.

Определение Решением системы (1) называется такая совокупность чисел k_i, при подстановке которых в систему вместо переменных x_i, каждое уравнение системы обращается в верное равенство.

Определение Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной , если она не имеет решений.

Определение Совместная система называется определённой, если она имеет единственное решение, и неопределённой, если она имеет более одного решения.

Определение Две системы называются равносильными, если они имеют одно и то же множество решений.

Запишем систему (1) в матричной форме.

Пусть где A – матрица коэффициентов при переменных (она называется матрицей системы), X – вектор–столбец переменных, B - вектор–столбец cсвободных членов.

Так как число столбцов матрицы A равно числу строк вектор–столбца X, то их произведение есть вектор–столбец. Его элементами являются левые части системы (1).

На основании определения равенства матриц систему (1) можно записать в так называемом матричном виде: AX = B. (2)

Определение Матричным уравнением называется уравнение, в котором роль неизвестной играет некоторая матрица Х.

Простейшими примерами таких уравнений могут служить уравнения AX=C; XB=C; AXB=C, где Х и С- прямоугольные матрицы равных размеров, А и В- квадратные матрицы соответствующих размеров. Если предположить, что и , то эти уравнения имеют единственные решения.

1) 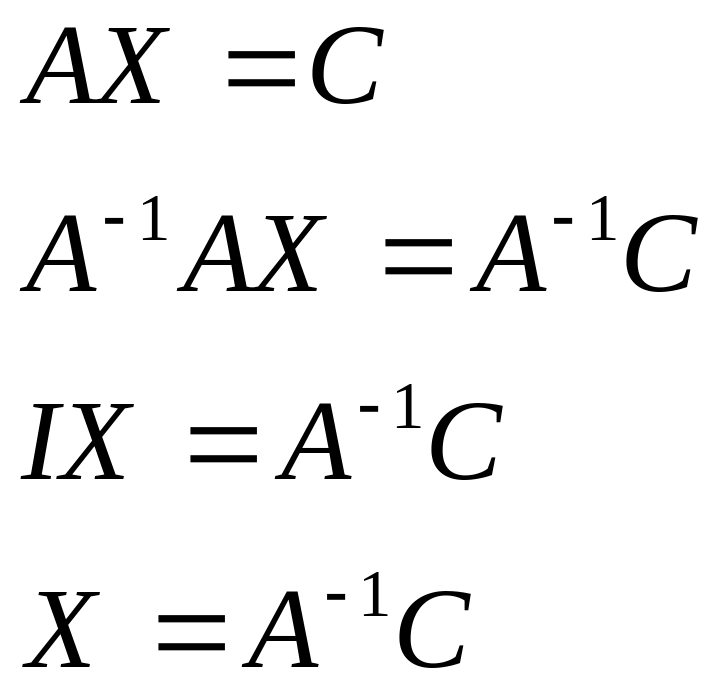2) 3)

Определение. Матрица системы, дополненная справа столбцом свободных членов, называется расширенной матрицей системы:

Теорема Кронекера–Капелли (необходимое и достаточное условие совместности системы линейных уравнений). Для того, чтобы система (1) была совместной, необходимо и достаточно, чтобы ранг матрицы A системы был равен рангу расширенной матрицы A^*.

Пример. Исследовать систему линейных уравнений на совместность:

.

Решение. Составим основную матрицу системы и найдем ее ранг:

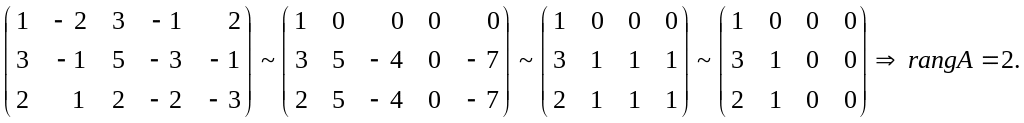
Составим расширенную матрицу системы и найдем ее ранг:

rangA rangA^*  по теореме Кронекера–Капелли система линейных уравнений несовместна.

7. Решение системы линейных уравнений методом обратной матрицы.

Пусть m=n. Тогда мы можем вычислить определитель системы det A. Предположим, что detA0. В этом случае выражение (2) можно рассматривать как матричное уравнение AX=B, которое имеет единственное решение X=A^-1B, которое и будет решением СЛУ.

Пример. Решить систему линейных уравнений:

Решение.

; det A = 15-1-8-4-3-10 = -11 ≠ 0  A^-1 существует.

Вычислим алгебраические дополнения элементов матрицы:

Обратная матрица равна .

Вектор-столбец неизвестных переменных равен произведению обратной матрицы и вектора-столбца свободных членов:

Следовательно, решением данной системы линейных уравнений будут числа: x=-1; y=3; z=2.