
- •1.Механическое движение как простейшая форма движения материи. Преставления о формах пространства и времени, лежащие в основе классической механики. Границы применимости классической механики.
- •2. Элементы кинематики материальной точки. Скорость и ускорение точки, как производные радиуса вектора по времени.
- •Кинематические уравнения движения
- •3) Нормальное и тангенциальное ускорения. Радиус кривизны траектории.
- •4.Элементы кинематики вращательного движения. Угловая скорость и угловое ускорение их связь с линейными скоростями и ускорениями точек вращающегося тела.
- •5. Динамика материальной точки и поступательного движения твёрдого тела. Сила. Закон инерции и инерциальные системы отсчета. Закон динамики материальной точки (2 и 3 законы Ньютона)
- •7.Работа консервативных и неконсервативных сил. Определение работы через интеграл, графически и через изменение энергии.
- •8. Кинетическая и потенциальные энергии. Понятие о градиенте потенциала. Закон сохранения механической энергии. Диссипация энергии. Консервативные и неконсервативные силы.
- •9. Поле как форма материи, осуществляющая силовое взаимодействие между частицами вещества. Вес и невесомость. Потенциальная энергия тяготения.
- •10. Применение законов сохранения к абсолютно неупругому удару. Энергия идущая на деформацию. Примеры неупругого удара.
- •11. Применение законов сохранения к абсолютно упругому удару. Частные случаи и их конкретные проявления.
- •12. Динамика вращательного движения абсолютно твердого тела. Момент силы. Основной закон вращательного движения. Момент инерции.
- •13.Момент инерции. Зависимость момента инерции твердого тела от его характеристик. Теорема Штейнера и ее применение на конкретном примере
- •14. Кинетическая энергия вращательного движения. Закон сохранения момента импульса и его проявление.
- •15. Неинерциальные системы отсчета. Силы инерции в поступательно движущейся неинерциальной системе. Эквивалентность сил инерции и гравитационных сил.
- •16. Силы инерции во вращающейся системе отсчета и их применение. Сила Кориолиса.
- •17. Преобразование координат Галилея. Механический принцип относительности. Закон сложения скоростей. Инварианты преобразования.
- •18. Постулаты специальной теории относительности. Преобразования Лоренца. Относительность одновременности.
- •20. Элементы релятивистской динамики. Закон взаимодействия массы и энергии. Изменение массы тела со скоростью. Границы применимости классической механики.
- •Релятивистский импульс
- •Закон взаимосвязи массы и энергии
- •Изменение массы тела со скоростью
- •Закон сложения скоростей
- •21) Термодинамический и молекулярно-кинетический методы исследования. Термодинамические параметры. Равновесные состояния и процессы, и их изображение на термодинамической диаграмме.
- •23. Число степеней свободы молекул. Закон равномерного распределения энергии по степеням свободы молекул. Внутренняя энергия идеального газа.
- •24) Работа газа при изменении его объема. Количество теплоты. Теплоемкость.
- •25.Первое начало термодинамики и применение его к изопроцессам. Работа в изопроцессах.
- •26. Применение первого начала термодинамики к адиабатному процессу. Уравнение Пуассона. Работа газа в адиабатном процессе.
- •27) Теплоемкость. Зависимость теплоемкости идеального газа от вида процесса. Свободная и связанная энергия.
- •28.Закон Максвелла для распределения молекул идеального газа по скоростям. Наиболее вероятная квадратичная и средняя арифметическая скорости молекул. Опытное подтверждение.
- •Барометрическая формула. Закон Больцмана для распределения частиц во внешнем потенциальном поле.
- •30) Среднее число столкновений и средняя длина свободного пробега молекул.
- •31.Явления переноса в термодинамически неравновестных системах. Коэффициент диффузии
- •32. Опытные законы теплопроводности и внутреннего трения. Коэффициенты теплопроводности и внутреннего трения
- •33) Обратимые и необратимые процессы. Круговые процессы (циклы) и их изображение на термодинамической диаграмме. Принцип Томпсона. Тепловые двигатели и холодильные машины.
- •34.Принцип Томсона. Цикл Карно и его кпд, работа за цикл. Ход цикла Карно в термодинамической диаграмме.
- •35.Второе начало термодинамики. Молекулярно-кинетическая картина равновесных состояний. Энтропия идеального газа.
- •36) Отступление от законов идеальных газов. Реальные газы. Силы и потенциальная энергия межмолекулярного взаимодействия. Эффективный диаметр молекул.
- •37.Уравнение Ван-дер-Вальса
- •38.Сравнение изотерм Ван-дер-Ваальса с экспериментальными. Критическое состояние.
- •39) Фазовые переходы I и II рода. Уравнение Клапейрона-Клаузиуса.
12. Динамика вращательного движения абсолютно твердого тела. Момент силы. Основной закон вращательного движения. Момент инерции.
Динамика вращательного движения.
Описанное
нами движение твердого тела относительно
неподвижной точки является основным
видом движения. Однако вычислить
вектор ![]() –
момент импульса системы относительно
произвольной точки – не просто: надо
знать шесть проекций (три задают положение
тела, три задают положение точки).
Значительно проще найти момент
импульса
тела,
вращающегося вокруг неподвижной оси
z
(рис. 6.4). В этом случае составляющие
–
момент импульса системы относительно
произвольной точки – не просто: надо
знать шесть проекций (три задают положение
тела, три задают положение точки).
Значительно проще найти момент
импульса
тела,
вращающегося вокруг неподвижной оси
z
(рис. 6.4). В этом случае составляющие ![]() –
момента внешних сил, направленные
вдоль x и y,
компенсируются моментами сил реакции
закрепления. Вращение вокруг
оси z происходит
только под действием Mz .
Пусть некоторое тело вращается вокруг
оси z (рис.
6.5).
–
момента внешних сил, направленные
вдоль x и y,
компенсируются моментами сил реакции
закрепления. Вращение вокруг
оси z происходит
только под действием Mz .
Пусть некоторое тело вращается вокруг
оси z (рис.
6.5).
|
|
Получим уравнение динамики для некоторой точки mi этого тела, находящегося на расстоянии Ri от оси вращения. При этом помним, что и направлены всегда вдоль оси вращения z, поэтому
![]() или
или ![]() .(в
обоих случаях в знаменателе стоит dt)
.(в
обоих случаях в знаменателе стоит dt)
Поскольку ![]() у
всех точек разная, введем вектор угловой
скорости
у
всех точек разная, введем вектор угловой
скорости ![]() ,
причем
,
причем ![]() .
Тогда
.
Тогда ![]() .
Так как тело абсолютно твердое, то в
процессе вращения mi
и Ri
останутся неизменными. Тогда
.
Так как тело абсолютно твердое, то в
процессе вращения mi
и Ri
останутся неизменными. Тогда
![]()
Обозначим Ii – момент инерции точки находящейся на расстоянии R от оси вращения:
|
|
(6.2.1) |
|
Момент инерции тела служит мерой инертности во вращательном движении. В общем случае тело состоит из огромного количества точек, и все они находятся на разных расстояниях от оси вращения. Момент инерции такого тела равен:
|
|
(6.2.2) |
|
Как
видно, момент инерции I –
величина скалярная.
Просуммировав (6.2.1) по всем i-м
точкам, получим ![]() или
или
|
|
(6.2.3) |
|
Это основное уравнение динамики тела,
вращающегося вокруг неподвижной оси.
(Сравним: ![]() –
основное уравнение динамики поступательного
движения тела).
Для момента импульса
тела,
вращающегося вокруг оси z,
имеем:
–
основное уравнение динамики поступательного
движения тела).
Для момента импульса
тела,
вращающегося вокруг оси z,
имеем:
|
|
(6.2.4) |
|
(Сравним: ![]() –
для поступательного движения).
При этом помним, что
и
-
динамические характеристики вращательного
движения, направленные всегда вдоль
оси вращения. Причем
определяется
направлением вращения, как и
,
а направление
зависит
от того, ускоряется или замедляется
вращение.
–
для поступательного движения).
При этом помним, что
и
-
динамические характеристики вращательного
движения, направленные всегда вдоль
оси вращения. Причем
определяется
направлением вращения, как и
,
а направление
зависит
от того, ускоряется или замедляется
вращение.
Момент силы.
Сила приложенная к твердому телу, которое может вращаться вокруг некоторой точки, создает момент силы. Действие момента силы аналогично действию пары сил.
 Момент
силы
Момент
силы
Момент силы относительно некоторой точки — это векторное произведение силы на кратчайшее расстояние от этой точки до линии действия силы.
Единица СИ момента силы:
1. |
[M]= Ньютон · метр |
Если: M — момент силы (Ньютон · метр), F — Приложенная сила (Ньютон), r — расстояние от центра вращения до места приложения силы (метр), l — длина перпендикуляра, опущенного из центра вращения на линию действия силы (метр), α — угол, между вектором силы F и вектором положения r, То
2. |
|
или в виде векторного произведения
М омент
силы — аксиальный
вектор. Он направлен
вдоль оси вращения.
Направление
вектора момента силы определяется
правилом буравчика, а величина его
равна M.
омент
силы — аксиальный
вектор. Он направлен
вдоль оси вращения.
Направление
вектора момента силы определяется
правилом буравчика, а величина его
равна M.
Основной закон вращательного движения.
![]() (1.10)
(1.10)
Уравнение
(1.10) – основной закон динамики вращательного
движения твердого тела. Величина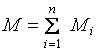 –
геометрическая сумма всех моментов
сил, то есть момент силы F,
сообщающий всем точкам тела ускорение
–
геометрическая сумма всех моментов
сил, то есть момент силы F,
сообщающий всем точкам тела ускорение ![]() .
. 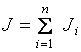 –
алгебраическая сумма моментов инерции
всех точек тела. Закон формулируется
так: «Момент силы, действующий на
вращающееся тело, равен произведению
момента инерции тела на угловое
ускорение».
–
алгебраическая сумма моментов инерции
всех точек тела. Закон формулируется
так: «Момент силы, действующий на
вращающееся тело, равен произведению
момента инерции тела на угловое
ускорение».
Момент инерции.
Момент инерции - величина, характеризующая распределения масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении.
Момент инерции тела относительно оси вращения зависит от массы тела и от распределения этой массы. Чем больше масса тела и чем дальше она отстоит от воображаемой оси, тем большим моментом инерции обладает тело. Момент инерции элементарной (точечной) массы mi, отстоящей от оси на расстоянии ri, равен:
![]() .
.
Момент инерции всего тела относительно оси равен:
![]()
или, для непрерывно распределенной массы:
![]()
Момент инерции всего тела сложной конфигурации обычно определяют экспериментально.
Момент инерции некоторых однородных твердых приведены в таблице 1.
Вычисление моментов инерции во многих случаях можно упростить, используя соображения симметрии и теорему Штейнера. Согласно теореме Штейнера момент инерции тела относительно какой-либо оси IA равен моменту инерции тела равен инерции тела относительно параллельной оси, проходящей через центр масс IC, сложенному с величиной ma2, где a - расстояние между осями:
IA = IC + ma2.
Понятием о моменте инерции широко пользуются при решении многих задач механики и техники.

 6,4
6,4 6,3
6,3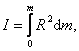 .
. M= F·l= F·r·sin(α)
M= F·l= F·r·sin(α)