9. Поле как форма материи, осуществляющая силовое взаимодействие между частицами вещества. Вес и невесомость. Потенциальная энергия тяготения.
Поле как форма материи.
Поля характеризуются тем, что работа, совершаемая действующими силами при перемещении м.т. из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений. Такие поля называются потенциальными, а силы, действующие в них – Консервативными. Если же работа, совершаемая силой, зависит от траектории перемещения м.т. из одной точки пространства в другую, то такие тела называются – Диссипативными(рассеивающими); их примером является сила трения.
Вес и невесомость.
Силу
тяжести 
с
которой тела притягиваются к Земле,
нужно отличать от веса
тела. Понятие веса
широко используется в повседневной
жизни.
Весом тела называют
силу, с которой тело вследствие его
притяжения к Земле действует на опору
или подвес. При
этом предполагается, что тело неподвижно
относительно опоры или подвеса.
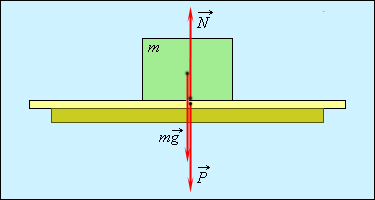
Пусть тело лежит на неподвижном
относительно Земли горизонтальном
столе (рис. 1.11.1). Систему отсчета,
связанную с Землей, будем считать инерциальной.
На тело действуют сила тяжести 
направленная
вертикально вниз, и сила упругости 
с
которой опора действует на тело.
Силу 
называют силой
нормального давления или силой
реакции опоры. Силы,
действующие на тело, уравновешивают
друг друга: 
В
соответствии с третьим законом Ньютона
тело действует на опору с некоторой
силой 
равной
по модулю силе реакции опоры и направленной
в противоположную сторону: 
По
определению, сила 
и
называется весом тела. Из приведенных
выше соотношений видно, что 
т. е.
вес тела
равен
силе тяжести 
Но
эти силы приложены к разным телам!
|
|
|
Вес
тела и сила тяжести. |
||
–
сила тяжести,
–
сила реакции опоры,
–
сила давления тела на опору (вес
тела). 
Если тело неподвижно висит на пружине, то роль силы реакции опоры (подвеса) играет упругая силы пружины. По растяжению пружины можно определить вес тела и равную ему силу притяжения тела Землей. Для определения веса тела можно использовать также рычажные весы, сравнивая вес данного тела с весом гирь на равноплечем рычаге.
Рассмотрим
теперь случай, когда тело лежит на опоре
(или подвешено на пружине) в кабине
лифта, движущейся с некоторым
ускорением 
относительно
Земли. Система отсчета, связанная с
лифтом, не является инерциальной. На
тело по-прежнему действуют сила
тяжести
и
сила реакции опоры 
но
теперь эти силы не уравновешивают друг
друга. По второму закону Ньютона
|
Сила
действующая
на опору со стороны тела, которую и
называют весом тела, по третьему закону
Ньютона равна 
Следовательно, вес
тела в ускоренно движущемся лифте есть
|
Пусть
вектор ускорения 
направлен
по вертикали (вниз или вверх). Если
координатную ось OY направить
вертикально вниз, то векторное уравнение
для
можно
переписать в скалярной форме:
|
P = m(g – a). |
(*) |
В этой
формуле величины P, g и a следует
рассматривать как проекции
векторов
, 
и
на
ось OY.
Так как эта ось направлена вертикально
вниз, g = const > 0,
а величины Pи a могут
быть как положительными, так и
отрицательными. Пусть, для определенности,
вектор ускорения
направлен
вертикально вниз, тогда a > 0 (рис. 1.11.2).
|
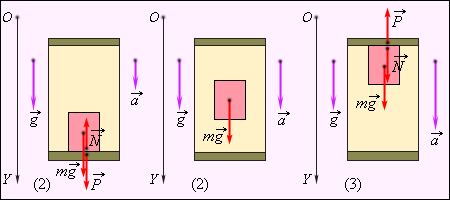
Вес тела в ускоренно движущемся лифте. Вектор ускорения направлен вертикально вниз. 1) a < g, P < mg; 2) a = g, P = 0 (невесомость); 3) a > g,P < 0 |
Из формулы (*) видно, что если a < g, то вес тела P в ускоренно движущемся лифте меньше силы тяжести. Если a > g, то вес тела изменяет знак. Это означает, что тело прижимается не к полу, а к потолку кабины лифта («отрицательный» вес). Наконец, если a = g, то P = 0. Тело свободно падает на Землю вместе с кабиной. Такое состояние называется невесомостью. Оно возникает, например, в кабине космического корабля при его движении по орбите при выключенными реактивных двигателями.
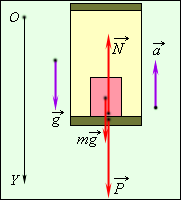
Если вектор ускорения направлен вертикально вверх (рис. 1.11.3), то a < 0 и, следовательно, вес тела всегда будет превышать по модулю силу тяжести. Увеличение веса тела, вызванное ускоренным движением опоры или подвеса, называют перегрузкой. Действие перегрузки испытывают космонавты, как при взлете космической ракеты, так и на участке торможения при входе корабля в плотные слои атмосферы. Большие перегрузки испытывают летчики при выполнении фигур высшего пилотажа, особенно на сверхзвуковых самолетах.
|
Рисунок 1.11.3. Вес тела в ускоренно движущемся лифте. Векторускорения направлен вертикально вверх. Вес тела приблизительно в два раза превышает по модулю силу тяжести (двукратная перегрузка) |
Потенциальная энергия тяготения.
Подъем тела вверх приводит к запасанию его потенциальной энергии тяготения. Уменьшение положения тела по высоте (падение) приводит к высвобождению запасенной энергии тяготения. Величина этой энергии равна: П |
отенциальная
энергия тяготения не зависит от формы
трактории, а зависит от его высоты
относительно нулевого уровня.
-
работа силы тяжести и изменение
потенциальной энергии тяготения.